11.2: Young's Modulus - Density Selection Map
- Page ID
- 8235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Imagine a material is needed to build an aircraft panel, this will be subject to bending moments, and so the deflection that occurs must be minimised. It is also necessary to keep the mass of the aircraft low and so the density of the material should also be minimised. It is important to find a balance between these different material properties in order to find the most suitable material for the application. This can be achieved by finding the appropriate merit index and comparing its value for different materials.
Consider the bending of a flat panel of length L, width w and height h, subject to an end load F. The engineering application sets the size of the panel (L and w) and the load it must support (F). Thus L, w and F are not variables in our analysis. On the other hand, the height h is a variable in that it is not of direct interest: it may be equally valid to use a thin panel of a dense material, or a thick panel of a light material. The bending moment M at the root of the beam is given by M = FL, and this decreases to zero at the end of the beam.
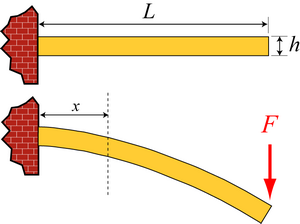
Cantilever bending
The second moment of area I (derivation) for such a panel is given by:
\[ I = \frac{w h^3}{12} \]
Assuming only simple bending occurs (and the panel only deflects as shown in the picture, i.e. not forming any complex shapes), the deflection of the end of the panel \(\delta\) is given by:
\[\delta = \frac{F L^3}{3 E I} \]
The mass m of the beam is given by:
\[m = Lwh \rho\]
Hence, having the height h as the free parameter, and combining the previous two equations by eliminating t gives:
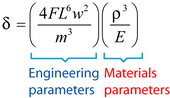
So to obtain the minimum deflection for a panel of free thickness and given mass, or equivalently the minimum mass for a given deflection, must be maximised. This is an example of a merit index. As the other values in the equation are engineering parameters, the material chosen will not alter these values, and so they are excluded from the merit index, which is based only on materials parameters.
Low density is clearly very important for this merit index and hence wood is favoured for applications requiring a flat sheet in bending as it has a low density due to the large voids contained in the structure.
This merit index can now be represented on a materials-selection map, allowing easy comparison of the different materials available for this application. Most materials-selection maps, such as the one shown, are plotted on logarithmic scales. This allows a given value of the index to be indicated by a straight line:
From the equation for deflection,
\[\frac{E^{1/3}}{\rho} = k\]
where \(k\) is a constant. Hence
\[\log (E) = 3 \log (\rho) + k'\]
where \(k'\) is a different constant \(3 \log (k)\)
On the selection map shown below, moving a line of the correct gradient as far as possible to the top and the left (and hence maximising \(E\) and minimising ρ) will give materials with the best value of the merit index. Try this by moving the line for the appropriate merit index on the following materials-selection maps for engineering alloys and biomaterials.
Other important merit indices used in relation to this chart are:
\[\frac{e}{\rho}\]
\[\frac{e}{\rho}\]
parameter, or the minimum deflection achievable on bending a beam with the width as a free parameter,
\[\frac{E^{1/2}}{\rho}\]
relating to the minimum deflection achievable on bending a beam with the cross sectional area (of fixed shape) as a free parameter.
It can be seen from the materials-selection chart that aluminum alloys behave well in bending, and hence are used in aeroplanes. Wood is also an impressive material for this application, and it was used in the past in the Mosquito aeroplane from World War II:

Mosquito aeroplane
Wood is able to resist bending with a low mass, as it has evolved so that trees will not bend far in strong winds or under their own weight. To maintain an array of leaves catching light for photosynthesis, tree trunks and branches have developed the materials properties of low density and relatively high Young’s modulus.


