2.1.10: Exercises

Last updated

Jun 6, 2021
Save as PDF
- 2.1.9: Summary
- 2.2: Network Topology- Nodes, Branches and Loops

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Analysis

1. For the circuit of Figure 3.10.1 , determine the circulating current.

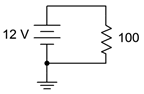
Figure 3.10.1

Answer 1

120mA

2. For the circuit of Figure 3.10.2 , determine the circulating current.

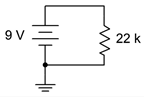
Figure 3.10.2

3. For the circuit of Figure 3.10.1 , determine the power dissipated in the resistor.

Answer 3

1.44W

4. For the circuit of Figure 3.10.2 , determine the power dissipated in the resistor.

5. Determine the voltage at the open terminals of Figure 3.10.3 .

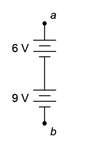
Figure 3.10.3

Answer 5

15 V

6. Determine the voltage at the open terminals of Figure 3.10.4 .

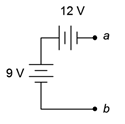
Figure 3.10.4

7. Determine the voltage at the open terminals of Figure 3.10.5 .

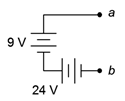
Figure 3.10.5

Answer 7

33 V

8. Determine the equivalent resistance of circuit shown in Figure 3.10.6 .

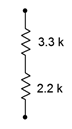
Figure 3.10.6

9. Determine the equivalent resistance of circuit shown in Figure 3.10.7 .

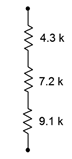
Figure 3.10.7

Answer 9

$2.6k\Omega$

10. Determine the equivalent resistance of circuit shown in Figure 3.10.8 .

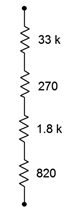
Figure 3.10.8

11. For the circuit of Figure 3.10.9 , determine the circulating current.

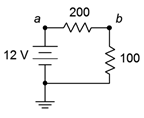
Figure 3.10.9

Answer 11

40 mA

12. For the circuit of Figure 3.10.9 , determine the voltages across each resistor and find $V_{ab}$ .

13. Given the circuit of Figure 3.10.9 , determine the power dissipated by each resistor and the power delivered by the source.

Answer 13

320mW (200 $\Omega$ )
160mW (100 $\Omega$ )
480mW (source)

14. For the circuit of Figure 3.10.10 , determine the circulating current.

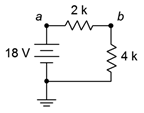
Figure 3.10.10

15. Given the circuit of Figure 3.10.10 , determine the voltages across each resistor and find $V_{ba}$ .

Answer 15

6V(2 $k\Omega$ )
12V(4 $k\Omega$ )
-6V ( $V_{ba}$ )

16. For the circuit of Figure 3.10.10 , determine the power dissipated by each resistor and the power delivered by the source.

17. For the circuit of Figure 3.10.11 , determine the circulating current.

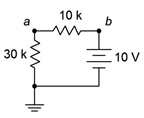
Figure 3.10.11

Answer 17

0.25 A

18. For the circuit of Figure 3.10.11 , determine the voltages across each resistor and find $V_a$ .

19. For the circuit of Figure 3.10.12 , determine the circulating current and indicate all voltage polarities.

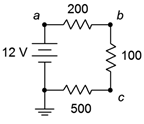
Figure 3.10.12

Answer 19

I = 15mA
$V_{ab}$ : + on left, - on right
$V_{bc}$ : + on top, - on bottom
$V_{c}$ : + on right, - on left
$V_{src}$ : + on top, - on bottom

20. Given the circuit of Figure 3.10.12 , determine the voltages across each resistor and find $V_b$ , $V_{bc}$ , and $V_{ca}$ .

21. For the circuit of Figure 3.10.12 , determine the power delivered by the source.

Answer 21

P = 180mW

22. For the circuit of Figure 3.10.13 , determine the circulating current and indicate all voltage polarities.

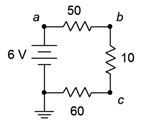
Figure 3.10.13

23. Given the circuit of Figure 3.10.13 , determine the voltages across each resistor and find $V_c$ , $V_{ac}$ , and $V_a$ .

Answer 23

$V_{50}=2.5V$
$V_{10}=0.5V$
$V_{60}=3V$
$V_{c}=3V$
$V_{ac}=3V$
$V_{a}=6V$

24. For the circuit of Figure 3.10.13 , determine the power dissipated by the 10 $\Omega$ resistor.

25. For the circuit of Figure 3.10.14 , determine the circulating current and indicate all voltage polarities.

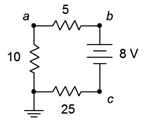
Figure 3.10.14

Answer 25

I = 200mA
$V_{5}$ : + on right, - on left
$V_{10}$ : + on top, - on bottom
$V_{25}$ : + on left, - on right
$V_{src}$ : + on top, - on bottom

26. For the circuit of Figure 3.10.14 , determine the voltages across each resistor and find $V_b$ , $V_c$ , and $V_{ca}$ .

27. Referring to the circuit of 3.10.15 , determine the voltages across each resistor and find $V_b$ , $V_c$ , and $V_{ac}$ .

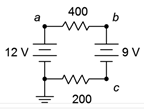
Figure 3.10.15

Answer 27

$V_{400}=2V$
$V_{200}=1V$
$V_{b}=10V$
$V_{c}=1V$
$V_{ac}=11V$

28. Referring to the circuit of Figure 3.10.15 , determine the circulating current and indicate all voltage polarities.

29. Given the circuit of 3.10.16 , determine the voltages across each resistor and find $V_b$ , $V_c$ , and $V_{ac}$ .

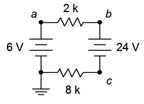
Figure 3.10.16

Answer 29

$V_{2k}=3.6V$
$V_{8k}=14.4V$
$V_{b}=9.6V$
$V_{c}=-14.4V$
$V_{ac}=20.4V$

30. Referring to the circuit of Figure 3.10.16 , determine the circulating current and indicate all voltage polarities.

31. Given the circuit of 3.10.17 , determine the circulating current and indicate all voltage polarities.

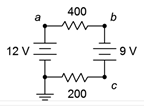
Figure 3.10.17

Answer 31

I = 35mA
$V_{400}$ : + on left, - on right
$V_{200}$ : + on right, - on left
$V_{12Vsrc}$ : + on top, - on bottom
$V_{9Vsrc}$ : + on bottom, - on top

32. Referring to the circuit of Figure 3.10.17 , determine the voltages across each resistor and find $V_b$ , $V_c$ , and $V_{ac}$ .

33. Given the circuit of 3.10.18 , determine the circulating current and indicate all voltage polarities.

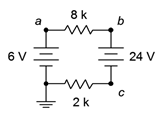
Figure 3.10.18

Answer 33

I = 1.89mA
$V_{2k}$ : + on left, - on right
$V_{8k}$ : + on right, - on left
$V_{6Vsrc}$ : + on top, - on bottom
$V_{24Vsrc}$ : + on top, - on bottom

34. Referring to the circuit of Figure 3.10.18 , determine the voltages across each resistor and find $V_b$ , $V_c$ , and $V_{ac}$ .

35. Using the voltage divider rule, determine the voltages $V_b$ , $V_c$ and $V_{ac}$ for the circuit shown in Figure 3.10.19 .

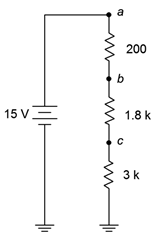
Figure 3.10.19

Answer 35

$V_{b} = 14.4V$
$V_{c} = 9V$
$V_{ac} = 6V$

36. Using the voltage divider rule, determine the voltages $V_b$ , $V_c$ and $V_{bd}$ for the circuit shown in Figure 3.10.20 .

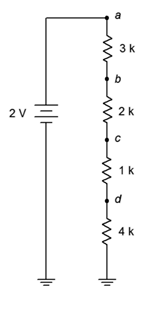
Figure 3.10.20

37. For the circuit of Figure 3.10.20 , determine $V_b$ if the 4 k $\Omega$ resistor is accidentally shorted. How does this compare to the original circuit?

Answer 37

$V_{b} = 1V$ . The 2V is now split across the three remaining resistors

38. For the circuit of Figure 3.10.20 , determine $V_b$ if the 4 k $\Omega$ resistor is accidentally opened. How does this compare to the original circuit?

39. Given the circuit shown in Figure 3.10.21 , find the voltage drop across the resistor.

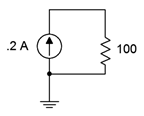
Figure 3.10.21

Answer 39

40. Given the circuit shown in Figure 3.10.22 , find the voltage drops across the resistor.

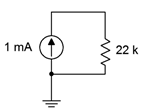
Figure 3.10.22

41. Find the voltage drops across the resistors in the circuit of Figure 3.10.23 .

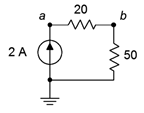
Figure 3.10.23

Answer 41

$V_{20} = 40V$
$V_{20} = 100V$

42. Find the voltage drops across the resistors in the circuit of Figure 3.10.24 .

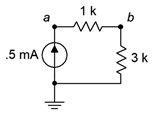
Figure 3.10.24

43. Find the voltage drops across the resistors in the circuit of Figure 3.10.25 .

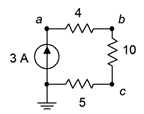
Figure 3.10.25

Answer 43

$V_{4} = 12V$
$V_{10} = 30V$
$V_{5} = 15V$

44. Find the voltage drops across the resistors in the circuit of Figure 3.10.26 .

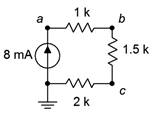
Figure 3.10.26

45. The circuit of Figure 3.10.27 uses a linear taper potentiometer. Determine $V_b$ when the wiper arm is at position $a$ , position $b$ , and at the halfway point.

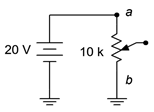
Figure 3.10.27

Answer 45

$V_{b} = 0V$ . This is true no matter where the wiper arm of the potentiometer is

46. What is the maximum current flowing through the potentiometer of Figure 3.10.27 ? At what position(s) does this occur?

Design

47. Redesign the circuit of Figure 3.10.1 using a new resistor such that the current from the 12 volt battery is 0.1 A.

Answer 47

Change the 100 $\Omega$ resistor to 120 $\Omega$

48. Redesign the circuit of Figure 3.10.2 using a new resistor such that the current from the 9 volt battery is 2 mA.

49. For the circuit of Figure 3.10.6 , find the value of a series voltage source that would generate 1 mA of current if it was connected across the terminals.

Answer 49

5.5V

50. For the circuit of Figure 3.10.8 , find the value of a series voltage source that would generate 1 mA of current if it was connected across the terminals.

51. Determine values for the resistors in Figure 3.10.28 such that $R_1$ is four times the size of $R_2$ and $R_2$ is three times the size of R3, with the total resistance equaling 8 k $\Omega$ .

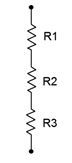
Figure 3.10.28

Answer 51

$R_{1} = 6k\Omega$
$R_{2} = 1.5k\Omega$
$R_{3} = 500\Omega$

52. For the circuit shown in Figure 3.10.29 , determine values for $R_1$ and $R_2$ such that $V_{ab}$ is 6 volts if $E$ is a 9 volt battery and the total current draw is 20 mA.

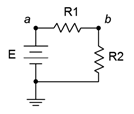
Figure 3.10.29

53. Consider the circuit shown in Figure 3.10.30 . If all resistors have the same value, determine that value if $E$ , a 24 volt source, generates a total power of 10 watts.

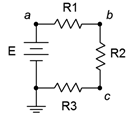
Figure 3.10.30

Answer 53

19.2 $\Omega$

54. For the circuit shown in Figure 3.10.31 , determine values for $R_1$ and $R_2$ such that $V_{ab}$ is 6 volts if $I$ is a 2 mA source and the total voltage drop is 24 volts.

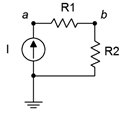
Figure 3.10.31

55. Consider the circuit of Figure 3.10.20 . Is it possible to add a fifth resistor such that the circulating current is 0.1 mA? If so, what is that resistor value?

Answer 55

Yes, 10 $k\Omega$

56. Consider the circuit of Figure 3.10.20 . Is it possible to add a fifth resistor such that the circulating current is 2 mA? If so, what is that resistor value?

Challenge

57. Assume that two AA cells, $E_1$ and $E_2$ , rated at 900 mAh each are used to drive a 2 watt lamp as shown in Figure 3.10.32 . Determine the expected life of the batteries.

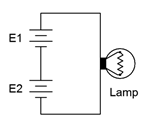
Figure 3.10.32

58. Given the circuit of Figure 3.10.33 , determine the required values of $E$ , $R_1$ , $R_2$ and $R_3$ if there is one volt across $R_3$ , the total current draw is 10 mA, the voltage across $R_1$ is twice the size of voltage across $R_2$ and the power dissipation in $R_2$ is 100 mW.

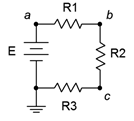
Figure 3.10.33

59. Given the circuit of Figure 3.10.33 , determine the required source voltage if $R_1$ is 1 k $\Omega$ , $R_2$ is 1 k $\Omega$ , the power dissipation in $R_1$ is 4 mW and the power dissipation in $R_3$ is 2 mW.

60. Given the circuit of Figure 3.10.34 , determine $V_c$ , $V_{db}$ and $V_{ce}$ .

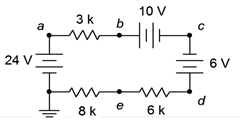
Figure 3.10.34

61. Given the circuit of Figure 3.10.34 , determine $V_{ac}$ , $V_{eb}$ and $V_d$ .

62. Refer to the circuit of Figure 3.10.20 . Assuming each resistor has a 10% tolerance, determine the maximum and minimum values for $V_c$ .

Simulation

63. Simulate the solution of design problem 43 and determine if the values produce the required results.

64. Perform a DC simulation on the circuit of Figure 3.10.13 and find all of the node voltages along with the circulating current.

65. Perform a DC simulation on the circuit of Figure 3.10.14 and find all of the node voltages along with the circulating current.

66. Perform a DC simulation on the circuit of Figure 3.10.26 and find all of the node voltages.

67. Perform a DC simulation on the circuit of Problem 34 and find all of the node voltages.

68. Perform a DC simulation on the circuit of Problem 36 and find all of the node voltages.

69. Simulate the solution of Challenge problem 58 and determine if the values produce the required results.

70. Simulate the circuit of Figure 3.10.34 (Challenge problems 60 and 61) and determine if the node voltages produced match the expected results.

71. Perform a Monte Carlo simulation on the circuit of Figure 3.10.19 . Set each resistor to 5% tolerance and run at least ten variations for $V_b$ to determine a typical spread of values.

Source: www.xkcd.com

Search

Text Color

Text Size

Margin Size

Font Type

Analysis

Design

Challenge

Simulation

Analysis

Design

Challenge

Simulation

Support Center

How can we help?