12.8: Cross Product and Torque
- Page ID
- 88003
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By Carey Smith
Cross product calculations are inherently 3-dimensional. The cross product of 2 vectors, a and b, is another vector, c, which is perpendicular to both a and b.
When a and b are parallel, c is zero.
When a and b are perpendicular, the magnitude of c = the product of the magnitudes of a and b.
Watch this video!
It gives a visual explanation of the cross product, including the right-hand rule. It also demonstrates the dot product.
.
Examples for parallel vectors, perpendicular vectors, and vectors at a 60 degree angle are given here. 3-D Plots are given for each example below, except for the zero case. These 3-D plots use the plot3() function. The plot3() function syntax is plot(x, y, z).
The cross product of parallel vectors is zero.
a = [1 2 3]
b = 2*a % = [2 4 6]
ab_cross = cross(a,b) % = [0 0 0]
Solution
Add example text here.
.
c1 = [1 0 0]
d1 = [0 1 0]
cd1_cross = cross(c1,d1)
% = [0 0 1]
% Plot each vector
figure;
plot3([0,c1(1)],[0,c1(2)],[0,c1(3)],'-*')
hold on;
plot3([0,d1(1)],[0,d1(2)],[0,d1(3)],'-o')
% Plot the cross-product vector on the same figure
plot3([0,cd1_cross(1)],[0,cd1_cross(2)],[0,cd1_cross(3)],'k-d')
axis equal
grid on;
xlabel('x')
ylabel('y')
zlabel('z')
% Use tools->Rotate 3D to verify that cd1_cross is orthogonal
% to the 1st 2 vectors and follows the right-hand rule.
title('cd1\_cross = cross(c1,d1), perpendicular')
Solution
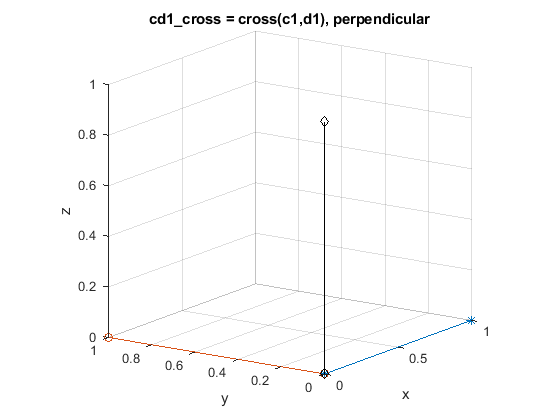
Add example text here.
.
c2 = [ 1 1 0] % at 45 degs
d2 = [ 1 -1 0] % at -45 degs
cd2_cross = cross(c2,d2) % = [0 0 -2]
% Plot each vector
figure;
plot3([0,c2(1)],[0,c2(2)],[0,c2(3)],'-*')
hold on;
plot3([0,d2(1)],[0,d2(2)],[0,d2(3)],'-o')
% Plot the cross-product vector on the same figure
plot3([0,cd2_cross(1)],[0,cd2_cross(2)],[0,cd2_cross(3)],'k-d')
axis equal
grid on;
xlabel('x')
ylabel('y')
zlabel('z')
% Use tools->Rotate 3D to verify that cd2_cross is orthogonal
% to the 1st 2 vectors and follows the right-hand rule.
title('cd2\_cross = cross(c2,d2), perpendicular')
Solution
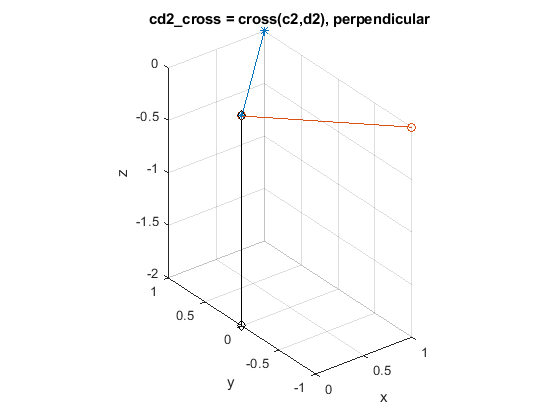
Add example text here.
.
e1 = [1 0 0] % at 0 degs
f1 = [cosd(60) sind(60) 0] % at 60 degs
% f = [0.500 0.866 0]
ef1_cross = cross(e1,f1)
% = [0 0 0.866]
% Plot each vector
figure;
plot3([0,e1(1)],[0,e1(2)],[0,e1(3)],'-*')
hold on;
plot3([0,f1(1)],[0,f1(2)],[0,f1(3)],'-o')
% Plot the cross-product vector on the same figure
plot3([0,ef1_cross(1)],[0,ef1_cross(2)],[0,ef1_cross(3)],'k-d')
axis equal
grid on;
xlabel('x')
ylabel('y')
zlabel('z')
% Use tools->Rotate 3D to verify that ef1_cross is orthogonal
% to the 1st 2 vectors and follows the right-hand rule.
title('ef2\_cross = cross(e1,f1), 60 degrees')
Solution
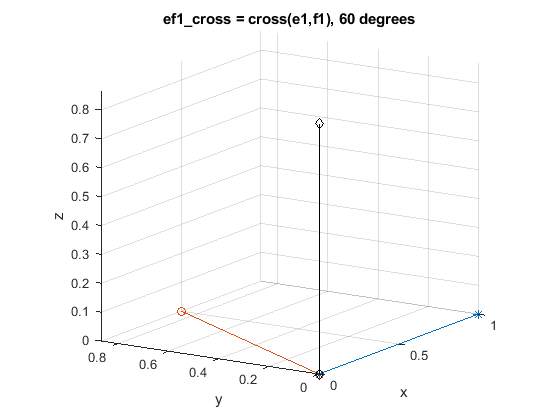
Add example text here.
.
Torque
For a lever of length R, and a Force, F, Torque = RxF (R cross F).
When the Force is in pounds and the length in feet, then the units are pound-feet.
When the Force is in Newtons and the length in meters, then the units are Newton-meters.
In mechanical engineering, torque is known as "moment".
This video illustrates torque nicely: (Cross Product for Calculating Torque, http://BigBangPhysics.com)
Consider a wrench loosening a bolt..
Our coordinate system is:
- x is horizontal in the plane of the wrench
- y is horizontal perpendicular to x (into the paper)
- z is vertical
[2 pts] Set up the force and wrench vectors:
A force is applied near the end of the wrench at a distance R = 0.20m from the bolt on the left side at a 20 degree angle from horizontal. When the bolt turns, it will have a counter-clockwise rotation.
R = 0.20*[-cosd(20), 0, sind(20)] %(m)
The magnitude of the force is 100N. The direction of the force is down.
F = 100*[0, 0, -1] %(N)
[4 pts] Compute the torque using the cross() function.
torque = cross(R,F)
[4 pts] Plot the R, F, and torque vectors on 1 figure using code similar to the cross product examples.
Since the units of R, F, and torque are all different, do not use "axis equal".
Add title('Torque')
Use tools->Rotate 3D to verify that the cross product is orthogonal to the R and F vectors and follows the right-hand rule
- Answer
-
Add texts here. Do not delete this text first.
.


