11.7.7.1: Choking explanation for pressure variation/reduction
- Page ID
- 827
Decreasing the pressure ratio or in actuality the back pressure, results in increase of the entrance and the exit velocity until a maximum is reached for the exit velocity. The maximum velocity is when exit Mach number equals one. The Mach number, as it was shown in Section 11.4, can increases only if the area increase. In our model the tube area is postulated as a constant therefore the velocity cannot increase any further. However, for the flow to be continuous the pressure must decrease and for that the velocity must increase. Something must break since there are conflicting demands and it result in a "jump'' in the flow. This jump is referred to as a choked flow. Any additional reduction in the back pressure will not change the situation in the tube. The only change will be at tube surroundings which are irrelevant to this discussion. If the feeding nozzle is a "converging–diverging'' then it has to be differentiated between two cases; One case is where the \(\dfrac{4\,f\,L}{D}\) is short or equal to the critical length. The critical length is the maximum \(\left.\dfrac{4\,f\,L}{D}\right|_{max}\) that associate with entrance Mach number.
Fig. 11.29 \(\,\) The pressure distribution as a function of \(\dfrac{4\,f\,L}{D}\) for a long \(\dfrac{4\,f\,L}{D}\).
Short \(\left.{4\,f\,L}\right/{D}\)
Figure 11.29 shows different pressure profiles for different back pressures. Before the flow reaches critical point \(a\) (in the Figure ) the flow is subsonic. Up to this stage the nozzle feeding the tube increases the mass flow rate (with decreasing back pressure). Pressure between point \(a\) and point \(b\) the shock is in the nozzle. In this range and further reduction of the pressure the mass flow rate is constant no matter how low the back pressure is reduced. Once the back pressure is less than point \(b\) the supersonic reaches to the tube. Note however that exit Mach number, \(M_2 < 1\) and is not \(1\). A back pressure that is at the critical point c results in a shock wave that is at the exit. When the back pressure is below point c , the tube is "clean'' of any The back pressure below point c} has some adjustment as it occurs with exceptions of point \textbf{d.
Fig. 11.30 The effects of pressure variations on Mach number profile as a function of \(\dfrac{4\,f\,L}{D}\) when the total resistance \(\dfrac{4\,f\,L}{D} = 0.3\) for Fanno Flow.
Long \(\dfrac{4\,f\,L}{D}\)
In the case of \(\dfrac{4\,f\,L}{D} > \left.\dfrac{4\,f\,L}{D}\right|_{max}\) reduction of the back pressure results in the same process as explained in the short \(\dfrac{4\,f\,L}{D}\) up to point \(c\). However, point \(c\) in this case is different from point c at the case of short tube \(\dfrac{4\,f\,L}{D} > \left.\dfrac{4\,f\,L}{D}\right|_{max}\). In this point the exit Mach number is equal to \(1\) and the flow is double shock. Further reduction of the back pressure at this stage will not "move'' the shock wave downstream the nozzle. At point \(c\) or location of the shock wave, is a function entrance Mach number, \(M_1\) and the "extra'' \(\dfrac{4\,f\,L}{D}\). The procedure is (will be) presented in later stage.
Fig. 11.31 Pressure ratios as a function of \(\dfrac{4\,f\,L}{D}\) when the total \(\dfrac{4\,f\,L}{D} = 0.3\).
Fig. 11.32 The extra tube length as a function of the shock location \(\dfrac{4\,f\,L}{D}\) Supersonic branch.
The Maximum Location of the Shock
The main point in this discussion however, is to find the furthest shock location downstream. Figure 11.32 shows the possible \(\Delta \left(4\,f\,L \over D \right)\) as a function of retreat of the location of the shock wave from the maximum location. When the entrance Mach number is infinity, \(M_1= \infty\), if the shock location is at the maximum length, then shock at \(M_x = 1\) results in \(M_y=1\). The proposed procedure is based on Figure 11.32 beginNormalEnumerate change startEnumerate=1
1. Calculate the extra \(\dfrac{4\,f\,L}{D}\) and subtract the actual extra \(\dfrac{4\,f\,L}{D}\) assuming shock at the left side (at the max length).
2. Calculate the extra \(\dfrac{4\,f\,L}{D}\) and subtract the actual extra \(\dfrac{4\,f\,L}{D}\) assuming shock at the right side (at the entrance).
3. According to the positive or negative utilizes your root finding procedure.
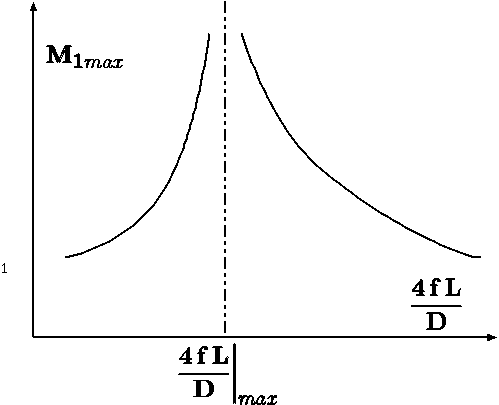
Fig. 11.33 The maximum entrance Mach number, \(M_1\) to the tube as a function of \(ld\) supersonic branch.
From numerical point of view, the Mach number equal infinity when left side assumes result in infinity length of possible extra (the whole flow in the tube is subsonic). To overcome this numerical problem, it is suggested to start the calculation from \(epsilon\) distance from the right hand side. Let denote
\[
\Delta \left( \dfrac{4\,f\,L}{D} \right ) = \bar{\dfrac{4\,f\,L}{D}}_{actual} -
\left.\dfrac{4\,f\,L}{D}\right|_{sup}
\label{fanno:eq:deltaFLD}
\]
\[
\left. \dfrac{4\,f\,L}{D} \right|_{retreat} = \left.\dfrac{4\,f\,L}{D}\right|_{max_{\infty}}
- \left.\dfrac{4\,f\,L}{D}\right|_{sup}
\label{fanno:eq:FLDretreat}
\]
Figure 11.33 shows the entrance Mach number, M1 reduces after the maximum length is exceeded.
Example 11.20
Calculate the shock location for entrance Mach number \(M_1 = 8\) and for \(\dfrac{4\,f\,L}{D} = 0.9\) assume that \(k = 1.4\) (\(M_{exit} = 1\))
Solution 11.20
The solution is obtained by an iterative process. The maximum \(\left.\dfrac{4\,f\,L}{D}\right|_{max}\) for \(k=1.4\) is 0.821508116. Hence, \(\dfrac{4\,f\,L}{D}\) exceed the maximum length \(\dfrac{4\,f\,L}{D}\) for this entrance Mach number. The maximum for \(M_1 =8\) is \(\dfrac{4\,f\,L}{D} = 0.76820\), thus the extra tube is \(\Delta \left( \dfrac{4\,f\,L}{D} \right) = 0.9 - 0.76820 = 0.1318\). The left side is when the shock occurs at \(\dfrac{4\,f\,L}{D} = 0.76820\) (flow is choked and no additional \(\dfrac{4\,f\,L}{D}\)). Hence, the value of left side is \(-0.1318\). The right side is when the shock is at the entrance at which the extra \(\dfrac{4\,f\,L}{D}\) is calculated for \(M_x\) and \(M_y\) is
| ShockWave | Input: \(M_2\) | k = 1.4 | |||
| \(M_x\) | \(M_y\) | \(\dfrac{T_y}{T_x}\) | \(\dfrac{\rho_y}{\rho_x}\) | \(\dfrac{P_y}{P_x}\) | \(\dfrac{{P_0}_y}{{P_0}_x}\) |
| 8.00 | 0.39289 | 13.3867 | 5.5652 | 74.50 | 0.00849 |
With \((M_1)'\)
| Fanno Flow | Input: \(\dfrac{4\,f\,L}{D}\) | k = 1.4 | |||
| \(\dfrac{4\,f\,L}{D}\) | \(\dfrac{P}{P^{\star}}\) | \(\dfrac{P_0} (click for details) \)Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/11:_Compressible_Flow_One_Dimensional/11.7:_Fanno_Flow/11.7.07:_The_Pressure_Ratio,_(left.P_2_right//_P_1),_effects/11.7.7.1:_Choking_explanation_for_pressure_variation//reduction), /content/body/center[1]/div[3]/div[2]/center[1]/table[2]/tbody/tr[2]/td[3]/span, line 1, column 4
|
\(\dfrac{\rho}{\rho^{\star} }\) | \(\dfrac{U}{U^{\star}}\) | \(\dfrac{T_0} (click for details) \)Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/11:_Compressible_Flow_One_Dimensional/11.7:_Fanno_Flow/11.7.07:_The_Pressure_Ratio,_(left.P_2_right//_P_1),_effects/11.7.7.1:_Choking_explanation_for_pressure_variation//reduction), /content/body/center[1]/div[3]/div[2]/center[1]/table[2]/tbody/tr[2]/td[6]/span, line 1, column 4
|
| 0.39289 | 2.4417 | 2.7461 | 1.6136 | 2.3591 |
0.42390 |
The extra \(\Delta\left(\dfrac{4\,f\,L}{D}\right)\) is \(2.442 - 0.1318 = 2.3102 \) Now the solution is somewhere between the negative of left side to the positive of the right side. In a summary of the actions is done by the following algorithm:
1. check if the \(\dfrac{4\,f\,L}{D}\) exceeds the maximum \(\left.{\dfrac{4\,f\,L}{D}}\right|_{max}\) for the supersonic flow. Accordingly continue.
2. Guess \(\left.{\dfrac{4\,f\,L}{D}}\right|_{up}= \dfrac{4\,f\,L}{D} - \left.\dfrac{4\,f\,L}{D}\right|_{max}\)
3. Calculate the Mach number corresponding to the current guess of \(\left.{\dfrac{4\,f\,L}{D}}\right|_{up}\),
4. Calculate the associate Mach number, \(M_x\) with the Mach number, \(M_y\) calculated previously,
5. Calculate \(\dfrac{4\,f\,L}{D}\) for supersonic branch for the \(M_x\)
6. Calculate the "new and improved'' \(\left.{\dfrac{4\,f\,L}{D}}\right|_{up}\)
7. Compute the "new \(\left.{\dfrac{4\,f\,L}{D}}\right|_{down} = {\dfrac{4\,f\,L}{D}} - \left.{\dfrac{4\,f\,L}{D}}\right|_{up}\)
8. Check the new and improved \(\left.\dfrac{4\,f\,L}{D}\right|_{down}\) against the old one.
9. Check the new and improved \(\left.\dfrac{4\,f\,L}{D}\right|_{down}\) against the old one. If it is satisfactory stop or return to stage b.
Shock location is:
| Fanno Flow | Input: \(M_1\) and \(\dfrac{4\,f\,L}{D}\) | k = 1.4 | |||
| \(M_1\) | \(M_2\) | \(\left.\dfrac{4\,f\,L}{D}\right|_{up}\) | \(\left.\dfrac{4\,f\,L}{D}\right|_{down}\) | \(M_x\) | \(M_y\) |
| 8.00 | 1.00 | 0.57068 | 0.32932 | 1.6706 | 0.64830 |
| Fanno Flow | Input: \(M_1\) and \(\dfrac{4\,f\,L}{D}\) | k = 1.4 | ||
| \(i\) | \(\left.\dfrac{4\,f\,L}{D}\right|_{up}\) | \(\left.\dfrac{4\,f\,L}{D}\right|_{down}\) | \(M_x\) | \(M_y\) |
| 0 | 0.67426 | 0.22574 | 1.3838 | 0.74664 |
| 1 | 0.62170 | 0.27830 | 1.5286 | 0.69119 |
| 2 | 0.59506 | 0.30494 | 1.6021 | 0.66779 |
| 3 | 0.58217 | 0.31783 | 1.6382 | 0.65728 |
| 4 | 0.57605 | 0.32395 | 1.6554 | 0.65246 |
| 5 | 0.57318 | 0.32682 | 1.6635 | 0.65023 |
| 6 | 0.57184 | 0.32816 | 1.6673 | 0.64920 |
| 7 | 0.57122 | 0.32878 | 1.6691 | 0.64872 |
| 8 | 0.57093 | 0.32907 | 1.6699 | 0.64850 |
| 9 | 0.57079 | 0.32921 | 1.6703 | 0.64839 |
| 10 | 0.57073 | 0.32927 | 1.6705 | 0.64834 |
| 11 | 0.57070 | 0.32930 | 1.6706 | 0.64832 |
| 12 | 0.57069 | 0.32931 | 1.6706 | 0.64831 |
| 13 | 0.57068 | 0.32932 | 1.6706 | 0.64831 |
| 14 | 0.57068 | 0.32932 | 1.670 | 0.64830 |
| 15 | 0.57068 | 0.32932 | 1.6706 | 0.64830 |
| 16 | 0.57068 | 0.32932 | 1.6706 | 0.64830 |
| 17 | 0.57068 | 0.32932 | 1.6706 | 0.64830 |
This procedure rapidly converted to the solution.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


