X-ray diffraction, Bragg's law and Laue equation
- Page ID
- 320
In November 1895, Wilhelm Röntgen discovered X-rays while working at the University of Wurzburg, Germany. Röntgen was investigating cathode rays in different types of evacuated glass tubes and trying to determine their range in air. He noticed that while the rays were being produced, a screen coated in fluorescent barium platinocyanide would glow. He was intrigued because the screen was too far from the tube to be affected by the cathode rays.
He assumed unknown rays, X-rays, were being emitted from the walls of the tube while the cathode ray tube was running. To his amazement, Röntgen found that the rays could pass straight through his hand and cast shadows of his bones on the fluorescent screen. He spent several weeks privately investigating the rays before publishing his results at the end of the year.
Bragg's Law
Bragg's law is the result of experiments derived by physicist Sir William Lawrence Bragg in 1912 and first presented on the same year to the Cambridge Philosophical Society.\(^{[1]}\) William Lawrence Bragg and his father, Sir William Henry Bragg, were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS, and diamond.
After Wilhelm Roentgen discovered X rays in 1895, William Henry Bragg pioneered the determination of crystal structure by X-RAY diffraction methods, began a lifelong investigation of the nature of radiation, principally X rays but also alpha and beta particles and gamma rays. After the discovery of the diffraction of X rays by crystals in 1912, Bragg and his son, William L., derived Bragg's law, which relates the wavelength of X rays to the glancing angle of reflection. In 1913 the elder Bragg built the first X-ray spectrometer, which he initially used to study X-ray spectral distributions. Within several years they were able to use this instrument and Bragg's law to derive the structure of crystals and show the exact positions of atoms. Subsequently, they demonstrated that the properties and behavior of a large variety of substances can be related to the position of their constituent atoms.
William Lawrence Bragg went on to become director of the Cavendish Laboratory in Cambridge England. It was at this lab, while he as director, in the early 1950's that J.D. Watson and F.H. C. Crick, using the X-ray diffraction techniques that Bragg pioneered, deduced the double helical structure of Deoxyribonucleic acid (DNA). Biotechnology has many forms today: Crime detection, forensic science, recombinant DNA to strengthen plants and animals as well as fetal analysis to detect birth defects just to name a few. None of these would be possible if Watson and Crick had not deduced the structure of DNA using X-ray diffraction. Just as the engineer who is building a tall building must understand steel and cement, a scientist must understand the double helix before she can build a molecule.\(^{[2]}\)
Although simple, Bragg's law confirmed the existence of real particles at the atomic scale, as well as providing a powerful new tool for studying crystals in the form of X-ray and neutron diffraction.

 \(^{[3]}\)
\(^{[3]}\)
In 1915, William Henry Bragg and William Lawrence Bragg were awarded the Nobel Prize for their contributions to crystal structure analysis. They were the first and (so far) the only father-son team to have jointly won the prize. Other father/son laureates include Niels and Aage Bohr, Manne and Kai Siegbahn, J. J. Thomson and George Thomson, Hans von Euler-Chelpin and Ulf von Euler, and Arthur and Roger Kornberg, who were all awarded the prize for separate contributions.
W. L. Bragg was 25 years old at the time, making him the youngest Nobel laureate to date.

W.H Bragg (1862-1942) and W.L. Bragg (1890-1971) on Swedish postage stamp.
1.2 The principle of Bragg’s Law and X-ray diffraction
\[\begin{align} n\lambda=2d\cdot\sin\theta \end{align} \label{1}\]
where
• n is an integer determined by the order given,
• λ is the wavelength of x-rays, and moving electrons, protons and neutrons,
• d is the spacing between the planes in the atomic lattice, and
• θ is the angle between the incident ray and the scattering planes.
Bragg diffraction occurs when electromagnetic radiation or subatomic particle waves with wavelength comparable to atomic spacings, are incident upon a crystalline sample, scattered by the atoms in the system and undergo constructive interference in accordance to Bragg's law. \(^{[2]}\)

Consider conditions necessary to make the phases of the beams coincide when the incident angle equals and reflecting angle. The rays of the incident beam are always in phase and parallel up to the point at which the top beam strikes the top layer at atom z. The second beam continues to the next layer where it is scattered by atom B. The second beam must travel the extra distance AB + BC if the two beams are to continue traveling adjacent and parallel. This extra distance must be an integral (\(n\)) multiple of the wavelength (\lambda\) for the phases of the two beams to be the same:
\begin{align} n\lambda=AB+BC \end{align}
Recognizing d as the hypotenuse of the right triangle Abz, we can use trigonometry to relate d and (\theta\) to the distance (AB + BC). The distance AB is opposite (\theta\) so,
\begin{align} AB=d\sin\theta \end{align}
Because \(AB = BC\), Equation (2) becomes,
\begin{align} n\lambda=2AB \end{align}
Substituting Equation (3) in Equation (4) we have,
\begin{align} n\lambda=2d\cdot\sin\theta \end{align}
and Bragg's Law has been derived.
Note that if only two rows of atoms are involved, the transition from constructive to destructive interference as \(\theta\) changes is gradual. However, if interference from many rows occurs, then the constructive interference peaks become very sharp with mostly destructive interference in between. This sharpening of the peaks as the number of rows increases is very similar to the sharpening of the diffraction peaks from a diffraction grating as the number of slits increases.
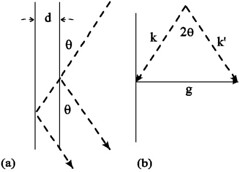
According to the figure on the right side above, we know the relation:
\begin{align} \overrightarrow{k}=\overrightarrow{k^{'}}+\overrightarrow{g} \end{align}
so
\begin{align} |\overrightarrow{g}|=2|\overrightarrow{k}|\sin\theta \end{align}
To ensure Bragg's Law, \(\overrightarrow{g}\) should be set to equal to \(\overrightarrow{G}\), where
Compare Equations (7) and (8), we have
So, only if
the Bragg's Law can be satisfied.\(^{[9]}\)
The definition of reciprocal lattice can be seen as follows:
In crystallography, the reciprocal lattice of a Bravais lattice is the set of all vectors \(\overrightarrow{k}\) such that:
\begin{align} \exp({i}\overrightarrow{k}\cdot\overrightarrow{r})=1 \end{align}
This reciprocal lattice is itself a Bravais lattice, and the reciprocal of the reciprocal lattice is the original real lattice.
1.3 The application of Bragg's Law—Bragg diffraction
Bragg diffraction (also referred to as the Bragg formulation of X-ray diffraction) was first proposed by William Lawrence Bragg and William Henry Bragg in 1913 in response to their discovery that crystalline solids produced surprising patterns of reflected X-rays (in contrast to that of, say, a liquid). They found that in these crystals, for certain specific wavelengths and incident angles, intense peaks of reflected radiation (known as Bragg peaks) were produced. W. L. Bragg explained this result by modeling the crystal as a set of discrete parallel planes separated by a constant parameter d. It was proposed that the incident X-ray radiation would produce a Bragg peak if their reflections off the various planes interfered constructively, just as what we showed above.
The concept of Bragg diffraction applies equally to neutron diffraction and electron diffraction processes.
1.3.1 X-ray diffraction

A diffraction pattern is obtained by measuring the intensity of scattered waves as a function of scattering angle. Very strong intensities known as Bragg peaks are obtained in the diffraction pattern when scattered waves satisfy the Bragg's Law.
Following Bragg's law, each dot (or reflection) in the diffraction pattern above forms from the constructive interference of X-rays passing through a crystal. The data can be used to determine the crystal's atomic structure.\(^{[4]}\)
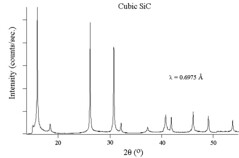
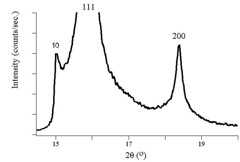
The figures above show experimental x-ray diffraction patterns of cubic SiC using synchrotron radiation. We can see Bragg peaks clearly from the figures.\(^{[5]}\)
1.3.2 Neutron diffraction

This is the neutron diffraction pattern of the Li0.86(Ni0.80Fe0.20)1.14O2 phase ( = 1.5939 Å). The difference between the observed and calculated profiles is given. The vertical bars show the Bragg reflections.\(^{[6]}\)
1.3.3 Electron Diffraction
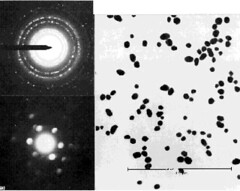
Electron diffraction provides a basis for studying the structure of crystals and of identifying materials. Metals tend to give very strong electron diffraction patterns, whereas biological specimens generally diffract quite weakly.
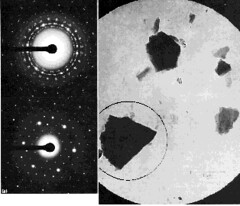
The figure above is electron diffraction patterns from selected small areas. The micrograph shows a field of crystalline particles outlined by a large selection aperture (6 µm at the specimen). The corresponding 'spotty ring' type of diffraction pattern (upper left) indicates that the crystals are oriented in a number of different directions. Using a smaller selecting aperture (2.3 µm at the specimen) positioned as indicated, the pattern is formed from the chosen crystal alone, giving the single-crystal pattern seen at lower left. \(^{[7]}\)
The patterns and explanation below are similar to the figure above, but the field of view is less than 1 µm across and hence too small for conventional s.a.d. A single particle has been selected for diffraction analysis by focusing the illumination into a spot covering the particle. The diffraction spots are discs rather than points because the electron beam is no longer parallel at the specimen, but a cone; each diffracted beam is therefore also a cone, which becomes a disc in the film plane. Discs can overlap and obscure others; hence, analysis of smaller crystals from µ-diffraction patterns is less precise than conventional s.a.d. \(^{[7]}\)
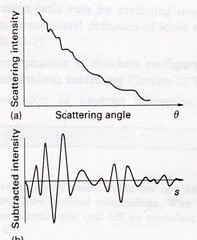
The figure below shows the scattering intensity as a function of the scattering angle of a gaseous sample. The gaseous sample presents all possible orientations of atom-atom separations to the electron beam and the resulting diffracting pattern is like an X-ray powder photograph. The intensity of the diffracted beam decreases steadily with increasing scattering angle and the overall pattern consists of a series of concentric undulations on a background.\(^{[8]}\)
1.5 References
- W.L. Bragg, "The Diffraction of Short Electromagnetic Waves by a Crystal", Proceedings of the Cambridge Philosophical Society, 17 (1913), 43–57.
- en.Wikipedia.org/wiki/Bragg%27s_law
- http://nobelprize.org/nobel_prizes/p...915/index.html
- The figure is from work of Jeff Dahl, and the figure is from www.goiit.com/posts/list/comm...tion-83055.htm
- This part is from Paul J. Schields, Center for High Pressure Research, Department of Earth & Space Sciences, State University of New York at Stony Brook, Stony Brook, NY 11794-2100.
- G. Prado, E. Suard, L. Fournes and C. Delmasb, "Cationic distribution in the Li1-z(Ni1-yFey)1+zO2 electrode materials", J. of Mater. Chem. 10 (2000) 2553
- "The principles and practice of electron microscopy", Ian M. Watt, 1997, Cambridge University Press
- perso.fundp.ac.be/%7Ejwouters...ffraction.html
- For more information about real and reciprocal crystal lattice, please also refer to Fangxiao's webpage:http://electrons.wikidot.com/paraelectric-and-antiferroelectric-properties
2. Laue Equation and its relation with Bragg's Law
Max Theodor Felix von Laue (9 October 1879 – 24 April 1960) was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals.\(^{[1]}\)

From 1909 to 1912, Laue was a Privatdozent at the Institute for Theoretical Physics, under Arnold Sommerfeld, at Ludwig Maximilians University of Munich(LMU). During the 1911 Christmas recess and in January 1912, Paul Peter Ewald was finishing the writing of his doctoral thesis under Sommerfeld. It was on a walk through the Englischer Garten in Munich in January, that Ewald told Laue about his thesis topic. The wavelengths of concern to Ewald were in the visible region of the spectrum and hence much larger than the spacing between the resonators in Ewald’s crystal model. Laue seemed distracted and wanted to know what would be the effect if much smaller wavelengths were considered. In June, Sommerfeld reported to the Physikalische Gesellschaft of Göttingen on the successful diffraction of x-rays by Laue, Paul Knipping and Walter Friedrich at LMU, for which Laue would be awarded the Nobel Prize in Physics, in 1914. While at Munich, he wrote the first volume of his book on relativity during the period 1910 to 1911. The Nobel Prize in Physics 1914:"for his discovery of the diffraction of X-rays by crystals"
After the discovery of the diffraction of X rays by crystals in 1912, Bragg and his son, William L., derived Bragg's law, which relates the wavelength of X rays to the glancing angle of reflection. In 1913 the elder Bragg built the first X-ray spectrometer, which he initially used to study X-ray spectral distributions. Within several years they were able to use this instrument and Bragg's law to derive the structure of crystals and show the exact positions of atoms. Subsequently, they demonstrated that the properties and behavior of a large variety of substances can be related to the position of their constituent atoms.
William Lawrence Bragg went on to become director of the Cavendish Laboratory in Cambridge England. It was at this lab, while he as director, in the early 1950's that J.D. Watson and F.H. C. Crick, using the X-ray diffraction techniques that Bragg pioneered, deduced the double helical structure of Deoxyribonucleic acid. (DNA)
Biotechnology has many forms today: Crime detection, forensic science, recombinant DNA to strengthen plants and animals as well as fetal analysis to detect birth defects just to name a few. None of these would be possible if Watson and Crick had not deduced the structure of DNA using X-ray diffraction. Just as the engineer who is building a tall building must understand steel and cement, a scientist must understand the double helix before she can build a molecule.\(^{[2]}\)
2.2 The principle of Laue Equation
2.2.1 Reciprocal space
All the reciprocal lattice points can be described by a linear combination of multiples of two basis vectors: \(\vec{b_1},\vec{b_2},\vec{b_3}\). Its definition is equivalent to the following relations:
\[\begin{align} \vec{b_{1}}=\frac{\vec{a_{2}}\times\vec{a_{3}}}{\vec{a_{1}}\cdot(\vec{a_{2}}\times\vec{a_{3}})} \end{align}\]
\[\begin{align} \vec{b_{2}}=\frac{\vec{a_{3}}\times\vec{a_{1}}}{\vec{a_{1}}\cdot(\vec{a_{2}}\times\vec{a_{3}})} \end{align}\]
An interesting property of the reciprocal lattice vector is that the relations are still valid if we replace lattice vectors by reciprocal lattice vectors and inversely reciprocal lattice vectors by lattice vectors. If \(V^{\ast}\) is the volume of the reciprocal unit cell, the reader can show that the expression \(VV^{\ast} = 1\) is also valid.
We can now define a reciprocal lattice vector \(\vec{h}\) by a linear combination of integer multiples of the three reciprocal lattice vectors:
We shall see later that the reciprocal vectors play an important role in diffraction. Before, lets us relate the reciprocal lattice vectors to some macroscopic properties of crystals.
Miller Indices
By construction, every reciprocal lattice vector is normal to a series of lattice planes. We know also that the faces of a crystal are parallel to lattice planes and therefore normal to the reciprocal vectors. We can therefore uniquely characterize each face of a crystal by the integer components of a reciprocal vector with one important subtlety. A face normal to vector \(\vec{h}\) cannot be distinguished from a normal to vector \(n\vec{h}\). Therefore, we shall characterize each face of a crystal by three integer components but without any common denominator. The triplet (h,k,l) satisfying this condition is called the Miller indices of the face. With this specification, we realize that Miller indices are only a subset of the possible reciprocal lattice vectors.

The figure above is an abstraction of a crystalline structure where only the nodes of the lattice are given. We have also reported a series of lattice planes with distances \(d_i\) and the corresponding normal \(\vec{h_i}\) to the series of planes. Without further demonstration we give here an important relation between the distances d and the reciprocal lattice vector \(\vec{h}\) normal to the series of equidistant planes :
Laue Equation in one dimension
Now that we have introduced the definition of the reciprocal lattice vectors, we are ready to express the physical law governing the diffraction of crystalline material. \(^{[3]}\)
Assume a row of scatterers separated by constant repeat, a. Radiation of wavelength \(\lambda\) is incident on this row at an angle \(\alpha_{0}\). Examine the the scatter from this row at an angle \(\alpha_{n}\). The path difference of rays scattering at points A and D is just AB-CD. If the incoming rays are in phase, the path difference must be some integral multiple of the wavelength for constructive interference to occur. This leads to the first Laue equation:
This result is valid for any scattered ray that makes an angle \(\alpha_{n}\) with the unit cell axis. Thus the Laue condition is consistent with a cone of scattered rays centered about the a axis.
This equation can be restated in vector terms. The repeat distance a, becomes a unit cell vector $\vec{a}$. Call a unit vector parallel to the incoming rays, $\vec{S_{0}}$, and one parallel to the scattered rays, \(\vec{S}\). There are then some simple vector dot products:
2.2.4 Laue Equation in three dimension
For a crystal with cell parameters \(\vec{a},\vec{b},\vec{c}\), we have three Laue equations:
where \(\cos\alpha_{0}\), \(\cos\beta_{0}\), \(\cos\gamma_{0}\) are the direction cosines of the incident ray, and \(\cos\alpha_{n}\), \(\cos\beta_{n}\), \(\cos\gamma_{n}\) are the direction cosines of the reflected ray in the crystal axis. So we must also satisfy:
Using that the angle between the incident and reflected ray is \(2\theta\)
Take \(\vec{k_{i}}\) to be the wavevector for the incoming (incident) beam and \(\vec{k_{o}}\) to be the wavevector for the outgoing (diffracted) beam. \(\vec{k_{o}}-\vec{k_{i}}=\Delta\vec{k}\) is the scattering vector and measures the change between the two wavevectors. Take \(\vec{a_{1}},\vec{a_{2}},\vec{a_{3}}\) to be the primitive vectors of the crystal lattice. The three Laue conditions for the scattering vector, or the Laue equations, for integer values of a reflection's reciprocal lattice indices (h,k,l) can be also written as follows:
These conditions say that the scattering vector must be oriented in a specific direction in relation to the primitive vectors of the crystal lattice.
In crystallography, the Laue equations give three conditions for incident waves to be diffracted by a crystal lattice. They can be reduced to the Bragg law as discussed in the following section.\(^{[1]}\)
2.3 The relation of Laue Equation to Bragg's Law
If \(\vec{G}=h\vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3}}\) is the reciprocal lattice vector, we know:
The Laue equations specify:
where
As a result, the diffraction condition can be derived as follows:
Considerring elastic scattering, we have:
Finally, we have:
So the diffraction condition \(2\vec{k_{i}}\cdot\vec{G}=|\vec{G}|^{2}$ reduces to the Bragg's law $2d\sin\theta=n\lambda\).\(^{[2]}\)
2.4 References
- en.Wikipedia.org/wiki/Max_von_Laue
- Jialan's another webpage:http://electrons.wikidot.com/x-ray-diffraction-and-bragg-s-law
- capsicum.me.utexas.edu/ChE386..._equations.htm
- Kittel, C. (1976). Introduction to Solid State Physics, New York: John Wiley & Sons. ISBN 0-471-49024-5
- W.L. Bragg, "The Diffraction of Short Electromagnetic Waves by a Crystal", Proceedings of the Cambridge Philosophical Society, 17 (1913), 43–57.
Contributors and Attributions
ContribMSE5317

