1.3: Structure of Communication Systems
- Page ID
- 1594
- An introduction to the fundamental model of communication, from the generation of the signal at the source through a noisy channel to reception of the signal at the sink.
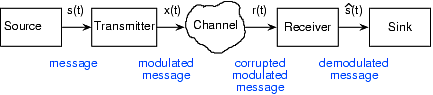
The fundamental model of communications is portrayed in Figure 1.3.1. In this fundamental model, each message-bearing signal, exemplified by s(t), is analog and is a function of time. A system operates on zero, one, or several signals to produce more signals or to simply absorb them (Figure 1.3.2). In electrical engineering, we represent a system as a box, receiving input signals (usually coming from the left) and producing from them new output signals. This graphical representation is known as a block diagram. We denote input signals by lines having arrows pointing into the box, output signals by arrows pointing away. As typified by the communications model, how information flows, how it is corrupted and manipulated, and how it is ultimately received is summarized by interconnecting block diagrams: The outputs of one or more systems serve as the inputs to others.

In the communications model, the source produces a signal that will be absorbed by the sink. Examples of time-domain signals produced by a source are music, speech, and characters typed on a keyboard. Signals can also be functions of two variables—an image is a signal that depends on two spatial variables—or more—television pictures (video signals) are functions of two spatial variables and time. Thus, information sources produce signals. In physical systems, each signal corresponds to an electrical voltage or current. To be able to design systems, we must understand electrical science and technology. However, we first need to understand the big picture to appreciate the context in which the electrical engineer works.
In communication systems, messages—signals produced by sources—must be recast for transmission. The block diagram has the message s(t) passing through a block labeled transmitter that produces the signal x(t). In the case of a radio transmitter, it accepts an input audio signal and produces a signal that physically is an electromagnetic wave radiated by an antenna and propagating as Maxwell's equations predict. In the case of a computer network, typed characters are encapsulated in packets, attached with a destination address, and launched into the Internet. From the communication systems “big picture” perspective, the same block diagram applies although the systems can be very different. In any case, the transmitter should not operate in such a way that the message s(t) cannot be recovered from x(t). In the mathematical sense, the inverse system must exist, else the communication system cannot be considered reliable. (It is ridiculous to transmit a signal in such a way that no one can recover the original. However, clever systems exist that transmit signals so that only the “in crowd” can recover them. Such cryptographic systems underlie secret communications.)
Transmitted signals next pass through the next stage, the evil channel. Nothing good happens to a signal in a channel: It can become corrupted by noise, distorted, and attenuated among many possibilities. The channel cannot be escaped (the real world is cruel), and transmitter design and receiver design focus on how best to jointly fend off the channel's effects on signals. The channel is another system in our block diagram, and produces r(t), the signal received by the receiver. If the channel were benign (good luck finding such a channel in the real world), the receiver would serve as the inverse system to the transmitter, and yield the message with no distortion. However, because of the channel, the receiver must do its best to produce a received message \[\hat{s}(t) \nonumber \]
that resembles s(t) as much as possible. Shannon showed in his 1948 paper that reliable—for the moment, take this word to mean error-free—digital communication was possible over arbitrarily noisy channels. It is this result that modern communications systems exploit, and why many communications systems are going “digital.” The module on Information Communication details Shannon's theory of information, and there we learn of Shannon's result and how to use it.
Finally, the received message is passed to the information sink that somehow makes use of the message. In the communications model, the source is a system having no input but producing an output; a sink has an input and no output.
Understanding signal generation and how systems work amounts to understanding signals, the nature of the information they represent, how information is transformed between analog and digital forms, and how information can be processed by systems operating on information-bearing signals. This understanding demands two different fields of knowledge. One is electrical science: How are signals represented and manipulated electrically? The second is signal science: What is the structure of signals, no matter what their source, what is their information content, and what capabilities does this structure force upon communication systems?


