1.5: Introduction Problems
- Page ID
- 1596
- Problems for introduction to signals and systems.
RMS Values
The rms (root-mean-square) value of a periodic signal is defined to be
\[s = \sqrt{\frac{1}{T}\int_{0}^{T}s^{2}(t)dt} \nonumber \]
where T is defined to be the signal's period: the smallest positive number such that
\[s(t)= s(t+T) \nonumber \]
- What is the period of
\[s(t)= A\sin (2\pi f_{0}t+\varphi ) \nonumber \]
- What is the rms value of this signal? How is it related to the peak value?
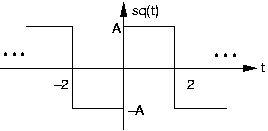
- What is the period and rms value of the depicted square wave, generically denoted by sq(t)?
- By inspecting any device you plug into a wall socket, you'll see that it is labeled "110 volts AC". What is the expression for the voltage provided by a wall socket? What is its rms value?
Modems
The word "modem" is short for "modulator-demodulator." Modems are used not only for connecting computers to telephone lines, but also for connecting digital (discrete-valued) sources to generic channels. In this problem, we explore a simple kind of modem, in which binary information is represented by the presence or absence of a sinusoid (presence representing a "1" and absence a "0"). Consequently, the modem's transmitted signal that represents a single bit has the form
\[x(t)= A\sin (2\pi f_{0}t), 0\leq t\leq T \nonumber \]
Within each bit interval T, the amplitude is either A or zero.
- What is the smallest transmission interval that makes sense with the frequency f0?
- Assuming that ten cycles of the sinusoid comprise a single bit's transmission interval, what is the datarate of this transmission scheme?Now suppose instead of using "on-off" signaling, we allow one of several different values for the amplitude during any transmission interval. If N amplitude values are used, what is the resulting data rate?
- The classic communications block diagram applies to the modem. Discuss how the transmitter must interface with the message source since the source is producing letters of the alphabet, not bits.
Advanced Modems
To transmit symbols, such as letters of the alphabet, RU computer modems use two frequencies (1600 and 1800 Hz) and several amplitude levels. A transmission is sent for a period of time T (known as the transmission or baud interval) and equals the sum of two amplitude-weighted carriers.
\[x(t)= A_{1}\sin (2\pi f_{1}t) + A_{2}\sin (2\pi f_{2}t), 0\leq t\leq T \nonumber \]
We send successive symbols by choosing an appropriate frequency and amplitude combination, and sending them one after another.
- What is the smallest transmission interval that makes sense to use with the frequencies given above? In other words, what should T be so that an integer number of cycles of the carrier occurs?
- Sketch (using Matlab) the signal that modem produces over several transmission intervals. Make sure you axes are labeled.
- Using your signal transmission interval, how many amplitude levels are needed to transmit ASCII characters at a datarate of 3,200 bits/s? Assume use of the extended (8-bit) ASCII code.
We use a discrete set of values for A1 and A2. If we have N1 values for amplitude A1, and N2 values for A2, we have N1N2 possible symbols that can be sent during each T second interval. To convert this number into bits (the fundamental unit of information engineers use to qualify things), compute:
\[\log _{2}(N_{1}N_{2}) \nonumber \]


