6.5: Line-of-Sight Transmission
- Page ID
- 1631
- Describes line-of-sight communication.
Long-distance transmission over either kind of channel encounters attenuation problems. Losses in wireline channels are explored in the Circuit Models module, where repeaters can extend the distance between transmitter and receiver beyond what passive losses the wireline channel imposes. In wireless channels, not only does radiation loss occur, but also one antenna may not "see" another because of the earth's curvature.
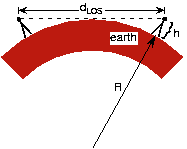
At the usual radio frequencies, propagating electromagnetic energy does not follow the earth's surface. Line-of-sight communication has the transmitter and receiver antennas in visual contact with each other. Assuming both antennas have height
\[d_{LOS}=2\sqrt{2hR+H^{2}}\simeq 2\sqrt{2Rh} \nonumber \]
where R is the earth's radius and R = 6.38×106 m.
Derive the expression of line-of-sight distance using only the Pythagorean Theorem. Generalize it to the case where the antennas have different heights (as is the case with commercial radio and cellular telephone). What is the range of cellular telephone where the handset antenna has essentially zero height?
Solution
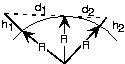
Use the Pythagorean Theorem,
\[(h+R)^{2}=R^{2}+d^{2} \nonumber \]
where h is the antenna height, d is the distance from the top of the earth to a tangency point with the earth's surface, and R the earth's radius. The line-of-sight distance between two earth-based antennae equals
\[d_{LOS}=\sqrt{2h_{1}R+h_{1}\, ^{2}}+\sqrt{2h_{2}R+h_{2}\, ^{2}} \nonumber \]
As the earth's radius is much larger than the antenna height, we have to a good approximation that
\[d_{LOS}=\sqrt{2h_{1}R}+\sqrt{2h_{2}R} \nonumber \]
If one antenna is at ground elevation, say \[h_{2}=0 \nonumber \] the other antenna's range is \[\sqrt{2h_{1}R} \nonumber \]
Can you imagine a situation wherein global wireless communication is possible with only one transmitting antenna? In particular, what happens to wavelength when carrier frequency decreases?
Solution
As frequency decreases, wavelength increases and can approach the distance between the earth's surface and the ionosphere. Assuming a distance between the two of 80 km, the relation λf = c gives a corresponding frequency of 3.75 kHz. Such low carrier frequencies would be limited to low bandwidth analog communication and to low datarate digital communications. The US Navy did use such a communication scheme to reach all of its submarines at once.
Using a 100 m antenna would provide line-of-sight transmission over a distance of 71.4 km. Using such very tall antennas would provide wireless communication within a town or between closely spaced population centers. Consequently, networks of antennas sprinkle the countryside (each located on the highest hill possible) to provide long-distance wireless communications: Each antenna receives energy from one antenna and retransmits to another. This kind of network is known as a relay network.


