6.14: Binary Phase Shift Keying
- Page ID
- 1866
- Introduces a method for representing bits with an analog signal known as binary phase shift keying.
A commonly used example of a signal set consists of pulses that are negatives of each other (See Figure 6.14.1 below).
\[s_{0}(t)=A_{P_{T}}(t) \nonumber \]
\[s_{1}(t)=-(A_{P_{T}}(t)) \nonumber \]

Here, we have a baseband signal set suitable for wireline transmission. The entire bit stream b(n) is represented by a sequence of these signals. Mathematically, the transmitted signal has the form
\[x(t)=\sum_{n\textbf{n}}(-1)^{b(n)} A_{P_{T}}(t-nT) \nonumber \]
and graphically Figure 6.14.2 below, shows what a typical transmitted signal might be.

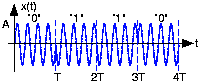
0110
The lower one shows an amplitude-modulated variant suitable for wireless channels.
This way of representing a bit stream---changing the bit changes the sign of the transmitted signal---is known as binary phase shift keying and abbreviated BPSK. The name comes from concisely expressing this popular way of communicating digital information. The word "binary" is clear enough (one binary-valued quantity is transmitted during a bit interval). Changing the sign of sinusoid amounts to changing---shifting---the phase by \(π\) (although we don't have a sinusoid yet). The word "keying" reflects back to the first electrical communication system, which happened to be digital as well: the telegraph.
The data rate \(R\) of a digital communication system is how frequently an information bit is transmitted. In this example it equals the reciprocal of the bit interval:
\[R=\frac{1}{T} \nonumber \]
Thus, for a 1 Mbps (megabit per second) transmission, we must have \(T = 1\, µs\).
The choice of signals to represent bit values is arbitrary to some degree. Clearly, we do not want to choose signal set members to be the same; we couldn't distinguish bits if we did so. We could also have made the negative-amplitude pulse represent a 0 and the positive one a 1. This choice is indeed arbitrary and will have no effect on performance assuming the receiver knows which signal represents which bit. As in all communication systems, we design transmitter and receiver together.
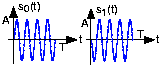
A simple signal set for both wireless and wireline channels amounts to amplitude modulating a baseband signal set (more appropriate for a wireline channel) by a carrier having a frequency harmonic with the bit interval.
\[s_{0}(t)=A_{P_{T}}(t)\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]
\[s_{1}(t)=-\left ( A_{P_{T}}(t)\sin \left ( \frac{2\pi kt}{T} \right )\right ) \nonumber \]
What is the value of \(k\) in this example?
Solution
k = 4
This signal set is also known as a BPSK signal set. We'll show later that indeed both signal sets provide identical performance levels when the signal-to-noise ratios are equal.
Write a formula, in the style of the baseband signal set as shown in the beginning of this section, for the transmitted signal as shown in the plot of the baseband signal set that emerges when we use this modulated signal.
Solution
\[x(t)=\sum_{n\textbf{n}}(-1)^{b(n)} A_{P_{T}}(t-nT)\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]
What is the transmission bandwidth of these signal sets? We need only consider the baseband version as the second is an amplitude-modulated version of the first. The bandwidth is determined by the bit sequence. If the bit sequence is constant—always 0 or always 1—the transmitted signal is a constant, which has zero bandwidth. The worst-case—bandwidth consuming—bit sequence is the alternating one shown in Figure 6.14.4. In this case, the transmitted signal is a square wave having a period of 2T.
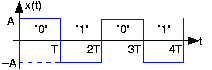
From our work in Fourier series, we know that this signal's spectrum contains odd-harmonics of the fundamental, which here equals 1/2T. Thus, strictly speaking, the signal's bandwidth is infinite. In practical terms, we use the 90%-power bandwidth to assess the effective range of frequencies consumed by the signal. The first and third harmonics contain that fraction of the total power, meaning that the effective bandwidth of our baseband signal is 3/2T or, expressing this quantity in terms of the datarate, 3R/2. Thus, a digital communications signal requires more bandwidth than the datarate: a 1 Mbps baseband system requires a bandwidth of at least 1.5 MHz. Listen carefully when someone describes the transmission bandwidth of digital communication systems: Did they say "megabits" or "megahertz"?
Show that indeed the first and third harmonics contain 90% of the transmitted power. If the receiver uses a front-end filter of bandwidth 3/2T , what is the total harmonic distortion of the received signal?
Solution
The harmonic distortion is 10%.
What is the 90% transmission bandwidth of the modulated signal set?
Solution
Twice the baseband bandwidth because both positive and negative frequencies are shifted to the carrier by the modulation: 3R


