13.1: Torque
- Page ID
- 18089
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
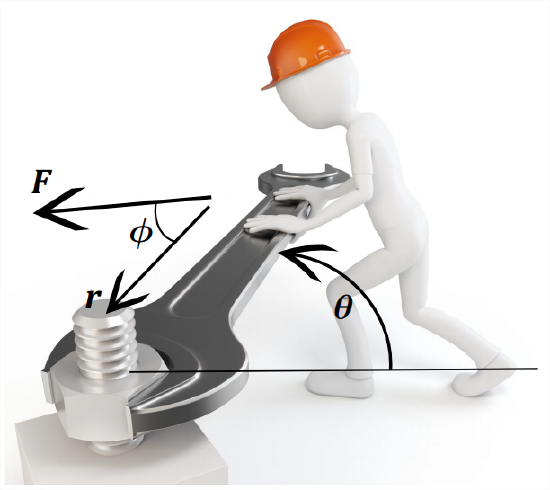
Newton’s second law \(\vec{F}=m\vec{a}\) has a rotational analogue. When a force \(\vec{F}\) is exerted at a location \(\vec{r}\) measured from some axis of rotation (e.g., the bolt in Figure \(\PageIndex{1}\)), then the cross product \(\vec{r}\times\vec{F}\) is called the torque, \(\vec{T}\). The cross product is defined in Equation 2.1.1, and is derived in detail in section D.3.1. For now, it is a vector perpendicular to both \(\vec{F}\) and \(\vec{r}\), with direction given by the right-hand rule. The magnitude is
\[|\vec{r}\times\vec{F}|=|\vec{r}||\vec{F}||\sin\phi| \nonumber \]
where \(\phi\) is the angle between \(\vec{r}\) and \(\vec{F}\).