Polymer Chemistry: Mechanical Properties
- Page ID
- 2907
The mechanical properties of polymers are one of the features that distinguishes them from small molecules.. The mechanical properties of a polymer involve its behavior under stress. These properties tell a polymer scientist or engineer many of the things he or she needs to know when considering how a polymer can be used.
- How strong is the polymer? How much can you stretch it before it breaks?
- How stiff is it? How much does it bend when you push on it?
- Is it brittle? Does it break easily if you hit it hard?
- Is it hard or soft?
- Does it hold up well under repeated stress?
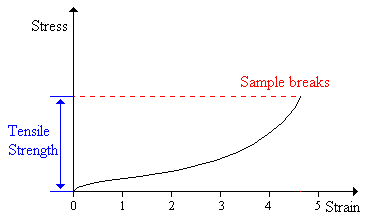
Tensile Strength
The tensile strength is the stress needed to break a sample45. It is expressed in Pascals or psi (pounds per square inch).
1 MPa = 145 psi
The tensile strength is an important property for polymers that are going to be stretched. Fibers, for instance, must have good tensile strength.
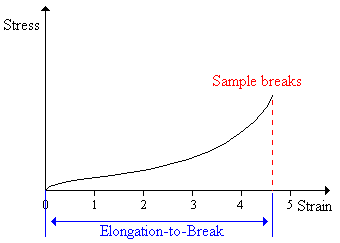
% Elongation to Break
The elongation-to-break is the strain on a sample when it breaks - this usually is expressed as a percent. The elongation-to-break sometimes is called the ultimate elongation. Fibers have a low elongation-to-break and elastomers have a high elongation-to-break47.
Young's Modulus
Young's modulus is the ratio of stress to strain. It also is called the modulus of elasticity or the tensile modulus. Young's modulus is the slope of a stress-strain curve. Stress-strain curves often are not straight-line plots, indicating that the modulus is changing with the amount of strain. In this case the initial slope usually is used as the modulus, as is illustrated in the diagram at the right.

Rigid materials, such as metals, have a high Young's modulus. In general, fibers have high Young's modulus values, elastomers have low values, and plastics lie somewhere in between.
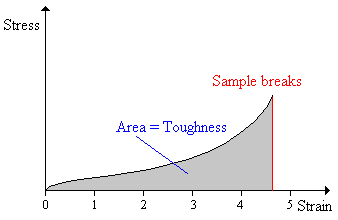
Toughness
The toughness of a material is the area under a stress-strain curve. The stress is proportional to the tensile force on the material and the strain is proportional to its length. The area under the curve then is proportional to the integral of the force over the distance the polymer stretches before breaking.
\[ Area \propto \int F(L) dL\]
This integral is the work (energy) required to break the sample. The toughness is a measure of the energy a sample can absorb before it breaks.
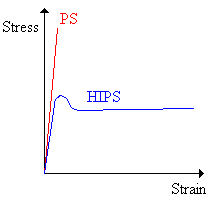
There is a difference between toughness and strength, as is illustrated in the three plots below.
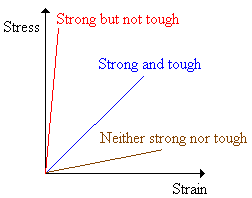
A material that is strong but not tough is said to be brittle. Brittle substances are strong, but cannot deform very much. Polystyrene (PS) is brittle, for example. High impact polystyrene (HIPS), a blend of polystyrene and polybutadiene (a rubbery polymer above its glass transition temperature) is said to be rubber-toughened.
Contributors and Attributions
David Whisnant (Wofford College). Partial support for this work was provided by the National Science Foundation's Division of Undergraduate Education through grants DUE #9950809 and DUE #9950296. Additional support was provided by the Camille and Henry Dreyfus Foundation.


