3.1: Data and information
- Page ID
- 20734
Previous chapter s have explained how information is organized in representations. A question that remains to be answered is what exactly constitutes information, i.e. what one should consider as information and data in these representations. This chapter introduces relevant theories and explains how they apply to building information and representations.
Theories and definitions
There is nothing more practical than a good theory: it supplies the definitions people need to agree what to do, how and why; it explains the world, providing new perspectives from where to see and understand it; it establishes targets for researchers keen to improve or refute the theory and so advance science and knowledge. In our case, there is a clear need for good, transparent and operational definitions. Terms like ‘information’ and ‘data’ are used too loosely, interchangeably and variably to remove ambiguities in information processing and management. Computerization adds to this vagueness, especially with subjects like buildings: as we have seen in previous chapters, there may be a big gap between the analogue representations still used in most AECO processes and the capacities of computers.
A theory that resolves these problems cannot draw from the AECO domains only. It needs a firm foundation in general theories of information, especially those that take the capacities and peculiarities of digital means and environments into account. Thankfully, there are enough candidates for this.
Syntactic, semantic and pragmatic theories
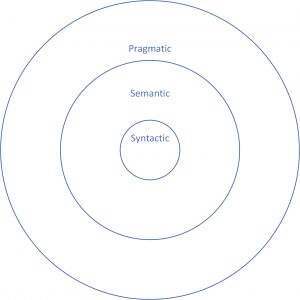
When one thinks of information theory in a computing context, Shannon’s MTC springs to mind.[1] The MTC is indeed foundational and preeminent among formal theories of information. It addresses what has been visualized as the innermost circle in information theory (Figure 1):[2] the syntactic core of information, dealing with the structure and basic, essential aspects of information, including matters of probability, transmission flows and capacities of communication facilities – the subjects of the technical side of information theory.
The outermost circle in the same visualization is occupied by pragmatics: real-life usage of meaningful information. Information management theories (which will be discussed in a later chapter) populate this circle, providing a general operational framework for supporting and controlling information quality and flow. To apply this framework, one requires pragmatic constraints and priorities from application areas: a notary and a facility manager have different interests with regard to the same building information.
Between the syntactic and the pragmatic lies the intermediate circle of semantics, which deals with how meaning is added to the syntactical components of information before they are utilized in real life. As syntactic approaches are of limited help with the content of information and its interpretation, establishing a basis for IM requires that we turn to semantic theories of information.
Arguably the most appealing of these is by Luciano Floridi, who is credited with establishing the subject of philosophy of information. His value goes beyond his position as a modern authority on the subject. The central role of semantics in his work is an essential contribution to the development of much-needed theoretical principles in a world inundated with rapidly changing digital technologies. In our case, they promise a clear and coherent basis for understanding AECO information and establishing parsimonious structures that link different kinds of information and data. These structures simplify IM in a meaningful and relevant manner: they allow us to shift attention from how one should manage information (the technical and operational sides) to which information and why.
Before moving on to explaining this theory and applying it to building information, it should be noted that management, computing and related disciplines abound with rather too easy, relational definitions of data, information, knowledge, strategy etc., e.g. that data interpreted become information, information understood turns into knowledge and so forth. Such definitions tend to underestimate the complexity of various cognitive processes and are therefore not to be trusted. In this book, we focus on data, information and their relation. The rest concerns utilization of information and benefits that may be derived for individuals, enterprises, disciplines or societies – matters that require extensive analyses well beyond the scope of the present book. Information certainly contributes to achieving these benefits and in many cases it may even be a prerequisite but seldom suffices by itself. Rather than making unfounded claims about knowledge and performance, we focus on more modest goals concerning IM: understanding building information, its quality and flows, and organizing them in ways that may help AECO take informed decisions, in the hope that informed also means better.
A semantic theory for building information
Data and information instances
A fundamental definition in Floridi’s theory[3] concerns the relation between data and information: an instance of information consists of one or more data which are well-formed and meaningful. Data are defined as lacks of uniformity in what we perceive at a given moment or between different states of a percept or between two symbols in a percept. For example, if a coffee stain appears on a floor plan drawing on paper (Figure 3), this is certainly a lack of uniformity with the earlier, pristine state of the drawing but it is neither well-formed nor meaningful within the context of architectural representations. It tells us nothing about the representation or the represented design, only that someone has been rather careless with the drawing (the physical carrier of the representation).


On the other hand, if the lack of uniformity between the two states is a new straight line segment across a room in a floor plan (Figure 4), this is both well-formed (as a line in a line drawing) and meaningful (indicating a change in the design, possibly that the room has now a split-level floor).

Data and information types
The typology of data is a key component in Floridi’s approach. Data can be:
- Primary, like the name and birth date of a person in a database, or the light emitted by an indicator lamp to show that a radio receiver is on.
- Anti–data,[4] i.e. the absence of primary data, like the failure of an indicator lamp to emit light or silence following having turned the radio on. Anti-data are informative: they tell us that e.g. the radio or the indicator lamp are defective.
- Derivative: data produced by other, typically primary data, which can therefore serve as indirect indications of the primary ones, such as a series of transactions with a particular credit card as an indication of the trail of its owner.
- Operational: data about the operations of the whole system, like a lamp that indicates whether other indicator lamps are malfunctioning.
- Metadata: indications about the nature of the information system, like the geographic coordinates that tell where a digital picture has been taken.
These types also apply to information instances, depending on the type of data they contain: an information instance containing metadata is meta-information.
In the context of analogue building representations like floor plans (Figure 5), lines denoting building elements are primary data. They describe the shape of these elements, their position and the materials they comprise.

In addition to such geometric primary data, an analogue floor plan may contain alphanumeric primary data, such as labels indicating the function of a room or dimension lines (Figure 6). A basic principle in hand drawing is that such explicitly specified dimensions take precedence over measurements in the drawing because amending these dimensions is easier than having to redraw the building elements.

Anti-data are rather tricky to identify in building representations because of the abstraction and ellipsis that characterize them. Quite often it is hard to know if something is missing in a representation. One should therefore consider absence as anti-data chiefly when absence runs contrary to expectation and is therefore directly informative: a door missing from the perimeter of a room indicates either a design mistake or that the room is inaccessible (e.g. a shaft). Similarly, a missing room label indicates either that the room has no specific function or that the drawer has forgotten to include it in the floor plan (Figure 7).

Derivative data in building representations generally refer to the abundance of measurements, tables and other data produced from primary data in the representation, such as floor area labels in a floor plan (Figure 8). One can recognize derivative data from the fact that they can be omitted from the representation without reducing its completeness or specificity: derivative data like the area of a room can be easily reproduced when necessary from primary data (the room dimensions). An important point is that one should always keep in mind the conventions of analogue representations, like the precedence of dimension lines over measurement in the drawing, which turns the former into primary data.

Operational data reveal the structure of the building representation and explain how data should be interpreted. Examples include graphic scale bars and north arrows, which indicate respectively the true size of units measured in the representation and the true orientation of shapes in the design (Figure 9).
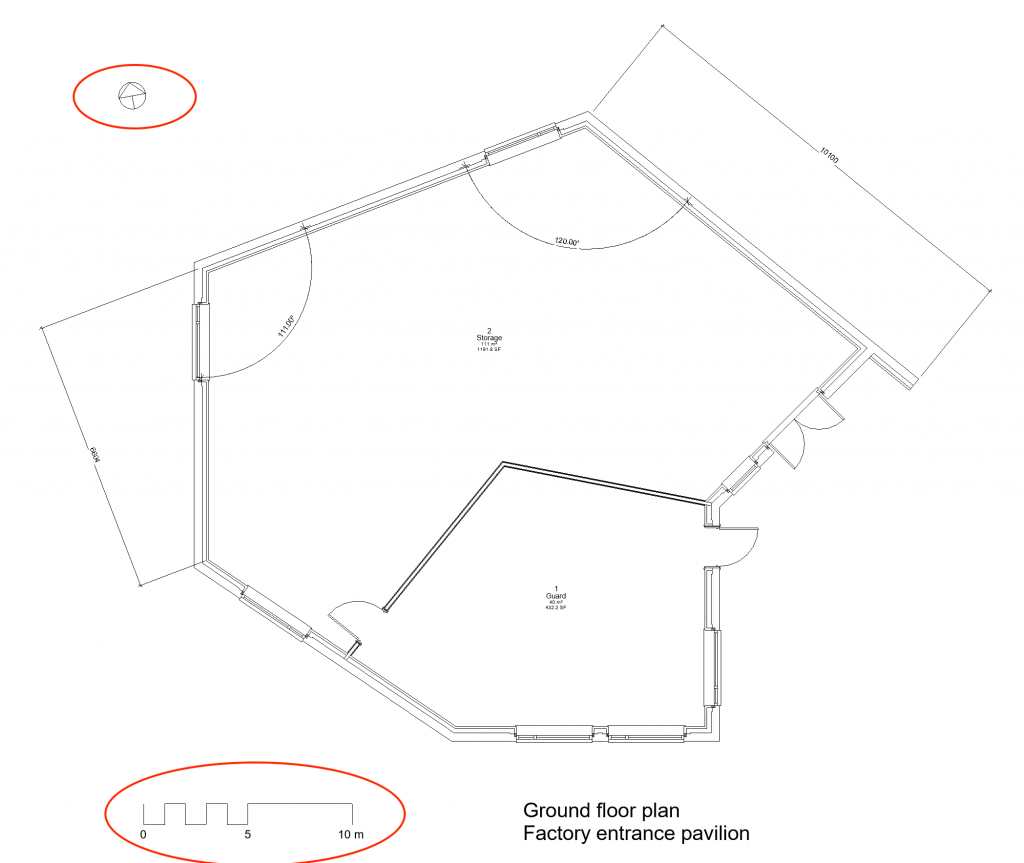
Finally, metadata describe the nature of the representation, such as the projection type and the design project or building, e.g. labels like ‘floor plan’ (Figure 10).

BIM, information and data
Data types in BIM
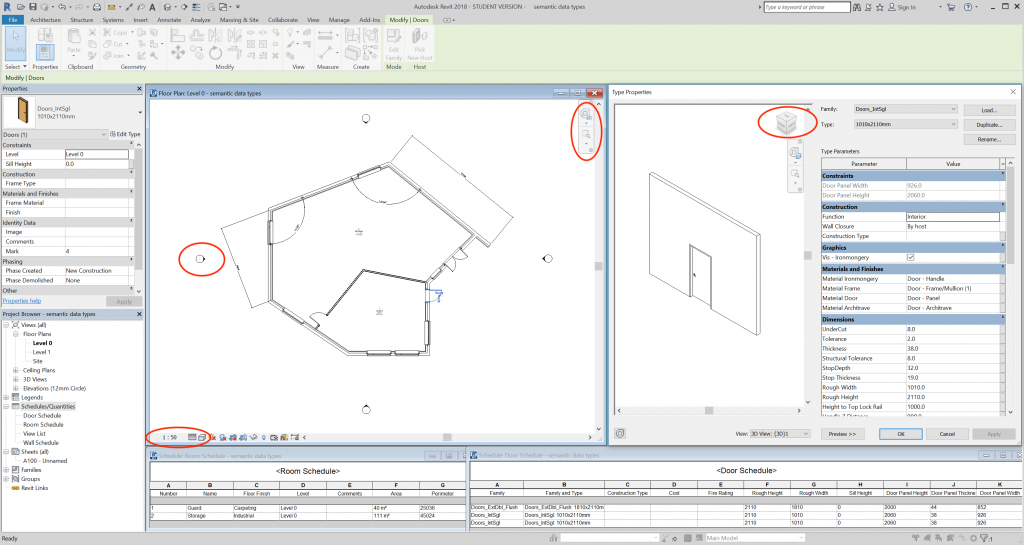
As we have seen in previous chapters, computerization does not just reproduce analogue building representations. Digital representations may mimic their analogue counterparts in appearance but can be quite different in structure – something that becomes apparent when we examine the data types they contain. Looking at a BIM editor on a computer screen, one cannot help observing a striking shift in primary and derivative data (Figure 11 & Figure 12): most graphic elements in views like floor plans are derived from properties of symbols. In contrast to analogue drawings, in BIM, dimension lines and values are derivative, pure annotations like floor area calculations in a space. This may be understandable given the ease with which one can modify a digital representation but even the lines denoting the various materials of a building element are derivative, determined by the type of the symbol: if the type of a wall changes, then all these graphic elements change accordingly. In analogue representations the opposite applies: we infer the wall type from the graphic elements that describe it in terms of layers of materials and other components.


The main exception is the geometry of symbols. As described in the previous chapter, when one enters e.g. a wall in BIM, the usual procedure is to first choose the type of the wall and then draw its axis in a geometric view like a floor plan. Similarly, modifications to the location or shape of the wall are made by changing the same axis, while other properties, like layer composition and material properties of each layer, can only be changed in the definition of the wall type. One can also change the axis by typing new coordinates in some window but in most BIM editors the usual procedure is interactive modification of the drawn axis with a pointer device like a mouse. Consequently, primary data may appear dispersed over a number of views and windows, including ones that chiefly contain derivative data.
One should not be confused by the possibilities offered by computer programs, especially for the modification of entities in a model. The interfaces of these programs are rich with facilities to change shapes and values. It seems as if programmers have taken the trouble to allow users to utilize practically everything for this purpose. For example, one may be able to change the length of a wall by typing a new value for its dimension line, i.e. via derivative data. Such redundancy of entry points is highly prized for user interaction but may be confusing in terms of IM, as it tends to obscure the type of data and the location where each type can be found. To reduce confusion and hence the risk of mistakes and misunderstandings, one should consider the character of each view or window and how necessary it is for defining an entity in a model. A schedule, for example, is chiefly meant for displaying derivative data, such as area or volume calculations, but may also contain primary data for reasons of overview, transparency or legibility. Most schedules are not necessary for entering entities in a model, in contrast to a window containing the properties of a symbol, from where one chooses the type of the entity to be entered. In managing the primary data of a symbol one should therefore focus on the property window and its contents.
Computer interfaces also introduce more operational data, through which users can interact with the software. Part of this interaction concerns how other data are processed, including in terms of appearance, as with the scale and resolution settings in drawing views mentioned in the previous chapter (Figure 13).
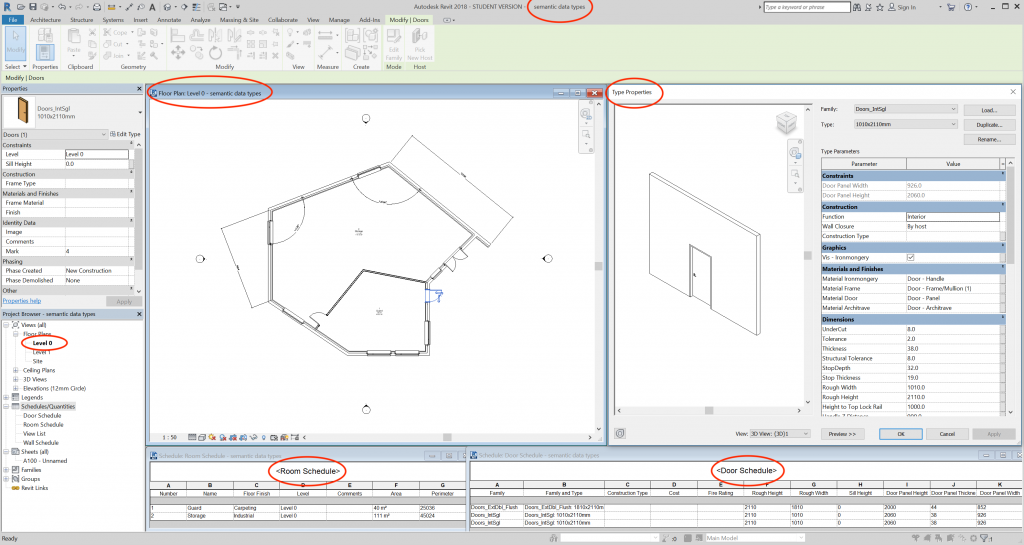
The presence of multiple windows on the screen also increases the number of visible metadata, such as window headers that describe the view in each window (Figure 14).
Anti-data remain difficult to distinguish from data missing due to abstraction or deferment. The lack of values for e.g. cost or fire rating for some building elements may merely indicate that their calculation has yet to take place, despite the availability of the necessary primary data. After all, both are calculated on the basis of materials present in the elements: if these materials are known, cost and fire ratings are easy to derive. One should remember the inherent duality of anti-data: they do not only indicate missing primary data but the presence of anti-data is significant and meaningful by itself. For example, not knowing the materials and finishes of a window frame, although the window symbol is quite detailed, signifies that the interfacing of the window to a wall is a non-trivial problem that remains to be solved. Interfacing typically produces anti-data, especially when sub-models meet in BIM, e.g. when the MEP and architectural sub-models are integrated, and the fastenings of pipes and cables to walls are present in neither. Anti-data generally necessitate action: no value (or “none”) for the demolition phase of an entity suggests that the entity has to be preserved during all demolition phases – not ignored but actively preserved with purposeful measures, which should be made explicit (Figure 15).

Information instances in BIM
Identifying information instances in BIM starts with recognizing the data. As described in the previous section, data are to be found in the symbols: their properties and relations. In the various views and windows of BIM software, one can easily find the properties of each symbol, either of the instance (Figure 16, Figure 18) or of the type (Figure 17).



What one sees in such a view or window is a mix of different data types, with derivative data like a volume calculation or thermal resistance next to primary data, such as the length and thickness of a wall. Moreover, no view or window contains a comprehensive collection of properties. As a result, when a property changes in one view, the change is reflected in several other parts of the interface that accommodate the same property or data derived from it.
Any lack of uniformity in these properties, including the addition of new symbols and their properties to a model, qualifies as data. One can restrict the identification of data to each view separately but it makes more sense for IM to include all clones of the same property, in any view. On the other hand, any derivative data that are automatically produced or modified as a result of the primary data count as different data instances. So, any change in the shape of a space counts as a single data instance, regardless of the view in which the user applies the change or of in how many views the change appears. The ensuing change in the space area value counts as a second instance of data; the change in the space volume as a third.
Relations between symbols are even more dispersed and often tacit. They can be found hidden in symbol behaviours (e.g. in that windows, doors or wash basins tend to stick to walls or in that walls tend to retain their co-termination), in explicit parametric rules and constraints, as well as in properties (e.g. construction time labels) that determine incidental grouping. Discerning lacks of uniformity in relations is therefore often hard, especially since most derive variably from changes in the symbols. For example, modifying the length of a wall may inadvertently cause its co-termination with another wall to be removed or, if the co-termination is retained, to change the angle between the walls.
Many relations can be made explicit and controllable through appropriate views like schedules. As we have seen, window and door schedules make explicit relations between openings and spaces. This extends to relations between properties of windows or doors and of the adjacent spaces, e.g. connects the fire rating of a door to whether a space on either side is part of a main fire egress route or the acoustic isolation offered by the door to the noise or privacy level of activities accommodated in either adjacent space.
Information instances can be categorized by the type of their data: primary, derivative, operational etc. This is important for IM, as it allows one to, firstly, prioritize in terms of significance and, secondly, to link information to actors and stakeholders. Primary information obviously carries a higher priority than derivative. Moreover, primary information (e.g. the shape of spaces) is produced or maintained by specific actors (e.g. designers), preferably with no interference by others who work with derivative information (e.g. fire engineers). So, information instances concerning space shape are fed forward from the designers to the fire engineers, whose observations or recommendations are fed back to the designers, who then initiate possible further actions and produce new data. Understanding these flows, the information types they convey and transparently linking instances to each other and to actors or stakeholders is essential for IM.
Another categorization of information instances concerns scope. This leads to two fundamental categories:
- Instances comprising one or more properties or relations of a single symbol: the data are produced when one enters the symbol in the representation or when the symbol is modified, either interactively by a user or automatically, e.g. on the basis of a built-in behaviour, parametrization etc. Instances of this category are basic and homogeneous: they refer to a single entity of a particular kind, e.g. a door. The entity can be:
- Generic in type, like an abstract internal door
- Contextually specific, such as a door for a particular wall in the design, i.e. partially defined by relations in the representation
- Specific in type, e.g. a specific model of a particular manufacturer, fixed in all its properties
- Instances comprising one or more properties or relations of multiple symbols, added or modified together, e.g. following a change of type for a number of internal walls, or a resizing or repositioning of the building elements bounding a particular space. Consequently, instances of this category can be:
- Homogeneous, comprising symbols of the same type, e.g. all office spaces in a building
- Heterogeneous, comprising symbols of various types, usually related to each other in direct, contextual ways, e.g. the spaces and doors of a particular wing that make up a fire egress route
These two categories can account for all data and abstraction levels in a representation, from sub-symbols (like the modification of the geometry of a door handle in the definition of a door type) to changes in the height of a floor level that affects the location of all building elements and spaces on that floor, the size and composition of some (e.g. stairs) and potentially also relations to entities on adjacent floors.
Key Takeaways
- An instance of information consists of one or more data which are well-formed and meaningful.
- Data are lacks of uniformity in what we perceive at a given moment or between different states of a percept or between two symbols in a percept.
- Data can be primary, anti-data, derivative, operational or metadata.
- There are significant differences between analogue and digital building representations concerning data types, with symbols like dimension lines being primary in the one and derivative in the other.
- In BIM lacks of uniformity can be identified in the properties and relations of symbols.
- Information instances can be categorized by the semantic type of their data and by their scope in the representation.
Exercises
- Identify the semantic data types in the infobox of a Wikipedia biographic lemma (the summary panel on the top right), e.g. https://en.Wikipedia.org/wiki/Aldo_van_Eyck (Figure 19),[5] and in the basic page information of the same lemma (e.g. https://en.Wikipedia.org/w/index.php...ck&action=info)

Figure 19. Infobox in Wikipedia


