1.6.2: Bulk Modulus
- Page ID
- 629
Similar to solids (hook's law), liquids have a property that describes the volume change as results of pressure change for constant temperature. It can be noted that this property is not the result of the equation of state but related to it. Bulk modulus is usually obtained from experimental or theoretical or semi theoretical (theory with experimental work) to fit energy–volume data. Most (theoretical) studies are obtained by uniformly changing the unit cells in global energy variations especially for isotropic systems ( where the molecules has a structure with cubic symmetries). The bulk modulus is a measure of the energy can be stored in the liquid. This coefficient is analogous to the coefficient of spring. The reason that liquid has different coefficient is because it is three dimensional verse one dimension that appear in regular spring.
The bulk modulus is defined as \[B_{T} = -v\left({\frac{\partial P}{\partial v}}\right)_{T}\] Using the identity of \(v = \frac{1}{\rho}\) transfers equation (34) into \[B_{T} = -\rho\left({\frac{\partial P}{\partial \rho}}\right)_{T}\] The bulk modulus for several selected liquids is presented in Table 1.5.
Table 1.5 The bulk modulus for selected material
| Chemical component | Bulk Modoulus \(10^{9}\dfrac{N}{m}\) | \(T_c\) | \(P_c\) |
| Acetic Acid | 2.49 | 593K | 57.8 [Bar] |
| Acetone | 0.80 | 508 K | 48 [Bar] |
| Benzene | 1.10 | 562 K | 4.74 [MPa] |
| Benzene | 1.10 | 562 K | 4.74 [MPa] |
| Carbon Tetrachloride | 1.32 | 556.4 K | 4.49 [MPa] |
| Ethyl Alcohol | 1.06 | 514 K | 6.3 [Mpa] |
| Gasoline | 1.3 | nf | nf |
| Glycerol | 4.03-4.52 | 850 K | 7.5 [Bar] |
| Mercury | 26.2-28.5 | 1750 K | 172.00 [MPa] |
| Methyl Alcohol | 0.97 | Est 513 | Est 78.5 [Bar] |
| Nitrobenzene | 2.20 | nf | nf |
| Olive Oil | 1.60 | nf | nf |
| Paraffin Oil | 1.62 | nf | nf |
| SAE 30 Oil | 1.5 | na | na |
| Seawater | 2.34 | na | na |
| Toluene | 1.09 | 591.79 K | 4.109 [MPa] |
| Turpentine | 1.28 | na | na |
| Water | 2.15-2.174 | 647.096 K | 22.064 [MPa] |
In the literature, additional expansions for similar parameters are defined. The thermal expansion is defined as \[\beta_{P} = \frac{1}{v}\left({\frac{\partial v}{\partial T}}\right)_{P}\] This parameter indicates the change of volume due to temperature change when the pressure is constant. Another definition is referred as coefficient of tension and it is defined as \[\beta_{v} = \frac{1}{P}\left({\frac{\partial P}{\partial T}}\right)_{v}\] This parameter indicates the change of the pressure due to the change of temperature (where \( v = constant\) These definitions are related to each other. This relationship is obtained by the observation that the pressure as a function of the temperature and specific volume as \[P = f\left(T, v\right)\] The full pressure derivative is \[dP = \left({\frac{\partial P}{\partial T}}\right)_{v}dT + \left({\frac{\partial P}{\partial v}}\right)_{T}dv\] On constant pressure lines, \(dP = 0\) and therefore equation (39) reduces to \[0 = \left({\frac{\partial P}{\partial T}}\right)_{v}dT + \left({\frac{\partial P}{\partial v}}\right)_{T}dv\] From equation (40), it follows that \[\frac{dv}{dT}l_{P=const} = -\frac{\left(\frac{\partial P}{\partial T}\right)_{v}}{\left(\frac{\partial P}{\partial v}\right)_{T}}\]
Equation (41) indicates that relationship for these three coefficients is \[\beta_{T} = -\frac{\beta_{v}}{\beta_{P}}\] The last equation (42) sometimes is used in measurement of the bulk modulus. The increase of the pressure increases the bulk modulus due to the molecules increase of the rejecting forces between each other when they are closer. In contrast, the temperature increase results in reduction of the bulk of modulus because the molecular are further away.
Example 1.10
Calculate the modulus of liquid elasticity that reduced 0.035 per cent of its volume by applying a pressure of 5[Bar] in a s slow process.
Solution 1.10
Using the definition for the bulk modulus
\[
\beta_T = - v \, \dfrac{\partial P }{\partial v} \simeq
\dfrac{v} {\Delta v} \, \Delta P = \dfrac {5}{0.00035} \simeq 14285.714 [Bar]
\]
Example 1.11
Calculate the pressure needed to apply on water to reduce its volume by 1 per cent. Assume the temperature to be \(20^{\circ}C\)
Solution 1.11
Using the definition for the bulk modulus
\[
\Delta P \sim \beta_T \dfrac{\Delta v}{v} \sim
2.15\,10^{9} ime 0.01 = 2.15\,10^{7} [N/m^2]
= 215 [Bar]
\]
Example 1.12
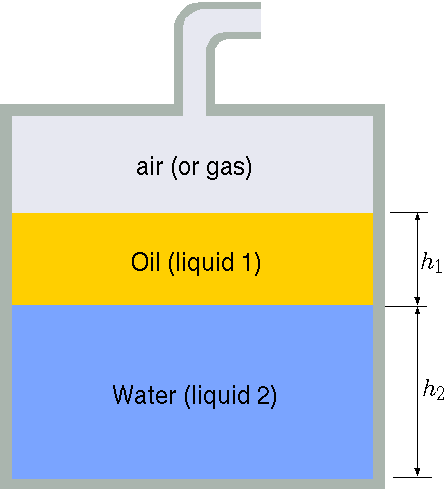
Fig. 1.16 Two liquid layers under pressure.
Initially the pressure in the tank is \(P_0\). The liquids are compressed due to the pressure increases. The new pressure is \(P_1\). The area of the tank is \(A\) and liquid A height is \(h_1\) and liquid B height is \(h_2\). Estimate the change of the heights of the liquids depicted in the Figure 1.16. State your assumptions.}
Solution 1.12
The volume change in a liquid is \[ \label{twoLiquid:1liquid} B_T \cong \dfrac{\Delta P }{ \Delta V /V} \] Hence the change for the any liquid is \[ \label{twoLiquid:DeltaH} \Delta h = \dfrac{\Delta P }{ A\, B_T/V} = \dfrac{h\, \Delta P}{B_T} \] The total change when the hydrostatic pressure is ignored. \[ \label{twoLiquid:totalH} \Delta h_{1+2} = \Delta P \left( \dfrac{h_1 }{{B_T}_1} + \dfrac{h_2 }{{B_T}_2} \right) \]
Example 1.13
In the Internet the following problem ( here with \(\LaTeX{}\) modification) was posted which related to Pushka equation.\
A cylindrical steel pressure vessel with volume 1.31 \(m^3\) is to be tested. The vessel is entirely filled with water, then a piston at one end of the cylinder is pushed in until the pressure inside the vessel has increased by 1000 kPa. Suddenly, a safety plug on the top bursts. How many liters of water come out?
Relevant equations and data suggested by the user were: \(B_T=0.2\times10^{10}N/m^2\), \(P_1=P_0+\rho\,g\,h\), \(P_1=-B_T\Delta V/V\) with the suggested solution of "I am assuming that I have to look for \(\Delta V\) as that would be the water that comes out causing the change in volume.''
\begin{align*}
\Delta V=\dfrac{-V\,\Delta P}{B_T}
=-1.31(1000)/(0.2\times10^{10})
\Delta V= 6.55*10^{-7}
\end{align*}
Another user suggest that:\ We are supposed to use the bulk modulus from our textbook, and that one is \(0.2\times10^{10}\). Anything else would give a wrong answer in the system. So with this bulk modulus, is 0.655L right?
In this post several assumptions were made. What is a better way to solve this problem.
Solution 1.13
It is assumed that this process can be between two extremes: one isothermal and one isentropic. The assumption of isentropic process is applicable after a shock wave that travel in the tank. If the shock wave is ignored (too advance material for this book.) the process is isentropic. The process involve some thermodynamics identities to be connected. Since the pressure is related or a function of density and temperature it follows that \[ \label{physicsForum:PrhoT} P = P \left( \rho, T \right) \] Hence the full differential is \[ \label{physicsForum:dP} dP = \left.\dfrac{\partial P }{ \partial \rho} \right|_T d\rho + \left.\dfrac{\partial P }{ \partial T} \right|_{\rho} dT \] This equation can be multiplied by \(\rho/P\) to be \[ \label{physicsForum:dPrhoP} \dfrac{ \rho\,dP}{P} = \dfrac{1}{P}\,\left( \overbrace{\rho\left.\dfrac{\partial P }{ \partial \rho} \right|_T}^{B_T} d\rho \right) + \rho\, \left( \overbrace{ \dfrac{1}{P} \left.\dfrac{\partial P }{ \partial T} \right|_{\rho} }^{\beta_v} dT \right) \] The definitions that were provided before can be used to write \[ \label{physicsForum:dPrhoP1} \dfrac{ \rho\,dP}{P} = \dfrac{1}{P}\, {B_T} \,d\rho + \rho\, \beta_v \, dT \] The infinitesimal change of density will be then \[ \label{physicsForum:drho1} \dfrac{1}{P}\, {B_T} \,d\rho = \dfrac{ \rho\,dP}{P} - \rho\, \beta_v \, dT \] or \[ \label{physicsForum:drho} d\rho = \dfrac{ \rho\,dP}{B_T} - \dfrac{\rho\,P\, \beta_v \, dT}{B_T} \] Thus, the calculation that were provide on line need to have corrections by subtracting the second terms.
jlkjdP=(∂P∂T)vdT+(∂P∂v)Tdv(39)


