1.7: Surface Tension
- Page ID
- 632
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)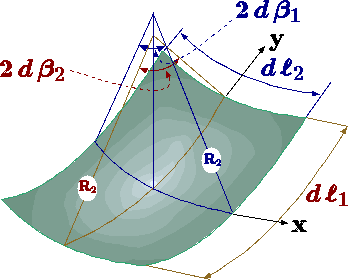
Figure 1.17. Surface tension control volume analysis describing principal radii.
The surface tension manifested itself by a rise or depression of the liquid at the free surface edge. Surface tension is also responsible for the creation of the drops and bubbles. It also responsible for the breakage of a liquid jet into other medium/phase to many drops (atomization). The surface tension is force per length and is measured by [N/m] and is acting to stretch the surface.
Surface tension results from a sharp change in the density between two adjoined phases or materials. There is a common misconception for the source of the surface tension. In many (physics, surface tension, and fluid mechanics) books explained that the surface tension is a result from unbalanced molecular cohesive forces. This explanation is wrong since it is in conflict with Newton's second law (see Example 1.14). This erroneous explanation can be traced to Adam's book but earlier source may be found.
Example 1.14
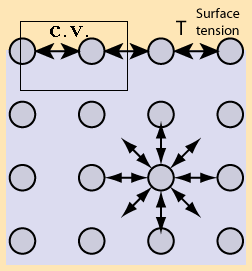
Fig. 1.18 Surface tension erroneous explanation.
"The cohesive forces between molecules down into a liquid are shared with all neighboring atoms. Those on the surface have no neighboring atoms above, and exhibit stronger attractive forces upon their nearest neighbors on the surface. This enhancement of the intermolecular attractive forces at the surface is called.'' Explain the fundamental error of this explanation (see Figure 1.18).
Solution 1.14
It amazing that this erroneous explanation is prevalent in physics and chemistry (check the standard books for general chemistry in any college). In fact, even in Wikipedia this erroneous explanation appears. The explanation based on the unbalance of the top layer of molecules. Consider the control volume shown in Figure 1.18. The control volume is made from a molecule thickness and larger width. If this explanation was to be believed it must obey Newton's Laws. However, as it will be shown, this explanation violates Newton's Laws and hence it is not valid. The entire liquid domain is in a static equilibrium and hence every element is static equilibrium including the control volume. The pulling on the left of control volume is balanced with forcing that pulling to the right. However, the control volume is pulled by the molecules below while there counter force to balance it. There are no molecules about to balance it. If this explanation was correct the top layer (control volume) was supposed to be balanced. According to Newton second Law this layer should move down and the liquid cannot be at rest ever. Obviously, the liquid is at rest and this explanation violates Newton second law. In the Dimensional Analysis Chapter, provide another reason why this explanation violate all what is known experimentally about the surface tension.
The relationship between the surface tension and the pressure on the two sides of the surface is based on geometry. Consider a small element of surface. The pressure on one side is \(P_{i}\) and the pressure on the other side is \(P_{0}\). When the surface tension is constant, the horizontal forces cancel each other because symmetry. In the vertical direction, the surface tension forces are puling the surface upward. Thus, the pressure difference has to balance the surface tension. The forces in the vertical direction reads \[\left(P_{i}-P_{0}\right)dll_{1}dll_{2} = \Delta P dll_{1}dll_{2} = 2\sigma dll_{1} \sin(\beta_{1}) + 2\sigma dll_{2} \sin(\beta_{2})\] For a very small area, the angles are very small and thus \(\left(\sin(\beta) \sim \beta \right)\) Furthermore, it can be noticed that \(dll_{i} \sim 2R_{i}d\beta_{i}\). Thus, the equation (47) can be simplified as \[\Delta P = \sigma \left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)\] Equation (48) predicts that pressure difference increase with inverse of the radius. There are two extreme cases: one) radius of infinite and radius of finite size. The second with two equal radii. The first case is for an infinite long cylinder for which the equation (48) is reduced to \[\Delta P = \sigma\left(\frac{1}{R}\right)\] Other extreme is for a sphere for which the main radii are the same and equation (48) is reduced to \[\Delta P = \frac{2\sigma}{R}\] Where \(R\) is the radius of the sphere. A soap bubble is made of two layers, inner and outer, thus the pressure inside the bubble is \[\Delta P = \frac{4\sigma}{R}\]
Example 1.15
A glass tube is inserted into bath of mercury. It was observed that contact angle between the glass and mercury is \(55^{\circ}\).
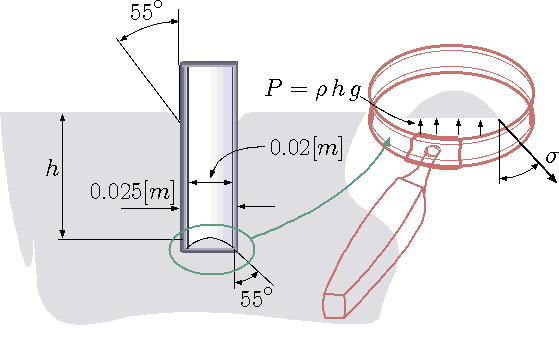
Fig. 1.19 Glass tube inserted into mercury.
Estimate the force due to the surface tension (tube is depicted in Figure 1.19). It can be assume that the contact angle is the same for the inside and outside part of the tube. Estimate the depression size. Assume that the surface tension for this combination of material is 0.5 [N/m]}
Solution 1.15
The mercury as free body that several forces act on it. \[ \label{tubeMercury:inside} F = \sigma 2\,\pi \cos55^\circ\,\left( {D_i} + {D_o} \right) \] This force is upward and the horizontal force almost canceled. However, if the inside and the outside diameters are considerable different the results is \[ \label{tubeMercury:horizontal} F = \sigma 2\,\pi \sin55\circ\,\left( {D_o} - {D_o} \right) \] The balance of the forces on the meniscus show under the magnified glass are \[ \label{tubeMercury:balance} P \, \overbrace{\pi\,r^2}^{A} = \sigma\,2\,\pi\,r + \cancelto{\sim0}{W} \] or \[ \label{tubeMercury:balanceF} g\,\rho\,h \, \pi\,r^2 = \sigma\,2\,\pi\,r + \cancelto{\sim0}{W} \] Or after simplification \[ \label{tubeMercury:balancea} h = \dfrac{2\,\sigma}{ g\,\rho\,r} \]
Example 1.16
A Tank filled with liquid, which contains \(n\) bubbles with equal radii, \(r\). Calculate the minimum work required to increase the pressure in tank by \(\Delta P\). Assume that the liquid bulk modulus is infinity.
Solution 1.16
The work is due to the change of the bubbles volume. The work is
\[
w = \int_{r_0}^{r_f} \Delta P(v) dv
\label{intro:eq:bubbleWork}
\]
\[
w = \int_{r_0}^{r_f} \overbrace{\dfrac{2\,\sigma}{r}}^{\Delta P}
\overbrace{4\,\pi\,r^2\,dr}^{dv}
= 8\, \pi\,\sigma \int_{r_0}^{r_f} r dr
= 4\,\pi\,\sigma \left( {r_f}^2 - {r_0}^2 \right)
\label{intro:eq:bubbleWork1}
\]
Where, \(r_0\) is the radius at the initial stage and \(r_f\) is the radius at the final stage. The work for n bubbles is then \(4\,\pi\,\sigma\,n\,\left( {r_f}^2 -
{r_0}^2 \right)\). It can be noticed that the work is negative, that is the work is done on the system.
Example 1.17
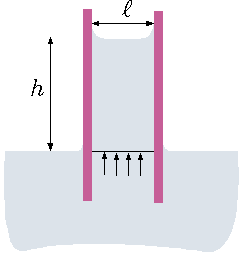
Fig. 1.20 Capillary rise between two plates.
1.20. Notice that previously a rise for circular tube was developed which different from simple one dimensional case. The distance between the two plates is \(ll\) and the and surface tension is \(\sigma\). Assume that the contact angle is \(0^{\circ}\) (the maximum possible force). Compute the value for surface tension of \(0.05[N/m]\), the density \(1000[kg/m^3]\) and distance between the plates of \(0.001[m]\).}
Solution 1.17
In Figure 1.20 exhibits the liquid under the current study. The vertical forces acting on the body are the gravity, the pressure above and below and surface tension. It can be noted that the pressure and above are the same with the exception of the curvature on the upper part. Thus, the control volume is taken just above the liquid and the air part is neglected. The question when the curvature should be answered in the Dimensional analysis and for simplification this effect is neglected. The net forces in the vertical direction (positive upwards) per unit length are
\[
\label{2DTubeRise:eq:gov}
2 \sigma \cos\,0^{\circ} = g\,h\,ll\,\rho \Longrightarrow h = \dfrac {2\,\sigma}{ll\,\rho\,g}
\]
\[
\label{2DTubeRise:eq:resutlts}
h = \dfrac {2\times 0.05}{0.001 \times 9.8\times \times 1000 } =
\]
Example 1.18
Develop expression for rise of the liquid due to surface tension in concentric cylinders.
Solution 1.18
The difference lie in the fact that "missing''cylinder add additional force and reduce the amount of liquid that has to raise. The balance between gravity and surface tension is \[ \label{hConcentricTube:gov} \sigma \, 2\,\pi\,\left(r_i\,\cos\theta_i + r_o\cos\theta_o\right) = \rho\,g\,h\, \left( \pi (r_o)^2 - \pi (r_i)^2 \right) \] Which can be simplified as \[ \label{hConcentricTube:results} h = \dfrac{2\,\sigma \left(r_i\,\cos\theta_i + r_o\cos\theta_o\right) } { \rho\,g\, \left((r_o)^2 - (r_i)^2 \right) } \] The maximum is obtained when \(\cos\theta_i = \cos\theta_o = 1\). Thus, the previous equation can be simplified \[ \label{hConcentricTube:resultsF} h = \dfrac{2\,\sigma } { \rho\,g\, \left(r_o - r_i \right) } \]
Template:HideTOC


