3.4.4: Product of Inertia
- Page ID
- 652
In addition to the moment of inertia, the product of inertia is commonly used. Here only the product of the area is defined and discussed. The product of inertia defined as \[I_{x_{i}x_{j}} = \int_{A} x_{i} x_{j} dA \] For example, the product of inertia for \(x\) and \(y\) axes is \[I_{xy} = \int_{A} x y dA \] Product of inertia can be positive or negative value as oppose the moment of inertia. The calculation of the product of inertia isn't different much for the calculation of the moment of inertia. The units of the product of inertia are the same as for moment of inertia.
Transfer of Axis Theorem
Same as for moment of inertia there is also similar theorem. \[I_{x'y'} = \int_{A} x'y'dA = \int_{A}\left(x + \Delta x\right) \left(y + \Delta y\right) dA \] expanding equation 49 results in \[I_{x'y'} = \int_{A} xydA + \int_{A} x\Delta ydA + \int_{A} \Delta xydA + \int_{A} \Delta x \Delta ydA\] The final form is \[I_{x'y'} = I_{xy} + \Delta x \Delta y dA \] There are several relationships should be mentioned \[I_{xy} = I_{yx}\] Symmetrical area has zero product of inertia because integration of odd function (asymmmertial function) left part cancel the right part.
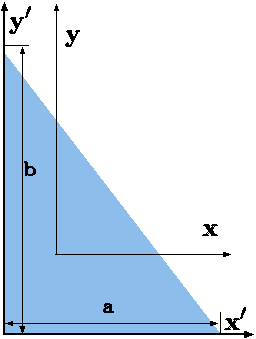
Fig. 3.13. Product of inertia for triangle.
Example 3.8
Calculate the product of inertia of straight edge triangle.
Solution 3.8
The equation of the line is
\[y = \dfrac{a}{b} x + a \]
\[I_{x^{'}y^{'}} = 0 +
\overbrace{\dfrac{a}{3}}^{\Delta x}
\overbrace{\dfrac{b}{3}}^{\Delta y}
\overbrace{\left(\dfrac{a\,b}{2}\right)}^{A}
= \dfrac{a^2\,b^2}{18} \]
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


