10.3 Potential Flow Functions Inventory
- Page ID
- 781
This section describes several simple scenarios of the flow field. These flow fields will be described and exhibits utilizition of the potential and stream functions. These flow fields can be combined by utilizing superimposing principle.
Uniform Flow
The trivial flow is the uniform flow in which the fluid field moves directly and uniformly from one side to another side. This flow is further simplified, that is the coordinates system aligned with to flow so the \(x\)–coordinate in the direction of the flow. In this case the velocity is given by
\[
\label{if:eq:UniformFlowUx}
\begin{array}{rl}
U_x = U_0 \\
U_y = 0
\end{array}
\]
\[
\label{if:eq:UFdef}
U_x = \dfrac{\partial \phi}{\partial x} =
\dfrac{\partial \psi}{\partial y} = U_0
\]
Hence, it can be obtained that
\[
\label{if:eq:UFps}
\begin{array}{rl}
\phi = U_0\,x + f_y(y) \
\psi = U_0\,x + f_x(x)
\end{array}
\]
where \(f_y(y)\) is arbitrary function of the \(y\) and \(f_x(x)\) is arbitrary function of \(x\). In the same time these function have to satisfy the condition
\[
\label{if:eq:UFcondition}
U_y = \dfrac{\partial \phi}{\partial x} \quad \text{and} \quad
-\dfrac{\partial \psi}{\partial x} = 0
\]
These conditions dictate that
\[
\label{if:eq:UFcondiRes}
\begin{array}{rl}
\dfrac{d\,f_y(y)}{dy} = 0 \\
\dfrac{d\,f_x(x)}{dx} = 0
\end{array}
\]
Hence
\[
\label{if:eq:UFSola}
f_y(y) = constant \Longrightarrow \phi = U_0 \, x + constant
\]
\[
\label{if:eq:UFSolb}
f_x(x) = constant \Longrightarrow \psi = U_0 \, y + constant
\]
These lines can be exhibits for various constants as shown in Figure below.
Fig. 10.6 Uniform Flow Streamlines and Potential Lines.
Line Source and Sink Flow
Another typical flow is a flow from a point or a line in a two dimensional field. This flow is only an idealization of the flow into a single point. Clearly this kind of flow cannot exist because the velocity approaches infinity at the singular point of the source. Yet this idea has its usefulness and is commonly used by many engineers. This idea can be combined with other flow fields and provide a more realistic situation.
Fig. 10.7 Streamlines and Potential lines due to Source or sink.
The volumetric flow rate (two dimensional) \(\dot{Q}\) denotes the flow rate out or in to control volume into the source or sink. The flow rate is shown in Figure 10.7 is constant for every potential line. The flow rate can be determined by
The volumetric flow rate (two dimensional) \(\dot{Q}\) denotes the flow rate out or in to control volume into the source or sink. The flow rate is shown in Figure 10.7 is constant for every potential line. The flow rate can be determined by
\[
\label{if:eq:sourceFlowRate}
\dot{Q} = 2\,\pi\,r\, U_r
\]
\[
\label{if:eq:potentialSource1}
\boldsymbol{\nabla} \phi = \mathbf{\pmb{U}} = U\,\mathbf{\widehat{r}} =
\dfrac{\dot{Q}}{ 2\,\pi\,r}\,\mathbf{\widehat{r}}
\]
Explicitly writing the gradient in cylindrical coordinate results as
\[
\label{if:eq:sourceGradient}
\dfrac{\partial \phi}{\partial r} \mathbf{\widehat{r}} +
\dfrac{1}{ r} \dfrac{\partial \phi}{\partial \theta} \mathbf{\widehat{\boldsymbol{\theta}} } +
\dfrac{\partial \phi}{\partial z} \mathbf{\widehat{z}} =
\dfrac{\dot{Q}}{ 2\,\pi\,r}\,\mathbf{\widehat{r}} + 0 \, \mathbf{\widehat{\boldsymbol{\theta}} }
+ 0 \, \mathbf{\widehat{z}}
\]
Equation (10) the gradient components must satisfy the following
\[
\label{if:eq:sourceComponents}
\begin{array}{rl}
\dfrac{\partial \phi}{\partial r} = \dfrac{\dot{Q}}{ 2\,\pi\,r}\,\mathbf{\widehat{r}} \\
\dfrac{\partial \phi}{\partial z} = \dfrac{\partial \phi}{\partial \theta} = 0
\end{array}
\]
The integration of equation results in
\[
\label{if:eq:sourcePotential}
\phi - \phi_0 = \dfrac{\dot{Q}}{ 2\,\pi\,r}\, \ln \dfrac{r}{r_0}
\]
where \(r_0\) is the radius at a known point and \(\phi_0\) is the potential at that point. The stream function can be obtained by similar equations that were used or Cartesian coordinates. In the same fashion it can be written that
\[
\label{if:eq:cylindricalIni}
d\psi = \mathbf{U} \mathbf{\cdot} \widehat{s} \,d\ell
\]
Where in this case \(d\ell = r\,d\theta\) (the shortest distance between two adjoining stream lines is perpendicular to both lines) and hence equation (13) is
\[
\label{if:eq:cylindrical}
d\psi = \mathbf{U} \mathbf{\cdot} \,r\,d\theta \,\mathbf{\widehat{r}} =
\dfrac{\dot{Q}}{ 2\,\pi\,r}\, r\,d\theta = \dfrac{\dot{Q}}{ 2\,\pi}\, \,d\theta
\]
Note that the direction of \(\mathbf{U}\) and \(\mathbf{\widehat{r}}\) is identical. The integration of equation (14) yields
\[
\label{if:eq:sourceStream}
\psi - \psi_0 = \dfrac{\dot{Q}}{ 2\,\pi\,r}\, \left( \theta -\theta_0\right)
\]
It traditionally chosen that the stream function \(\psi_0\) is zero at \(\theta=0\). This operation is possible because the integration constant and the arbitrary reference. In the case of the sink rather than the source, the velocity is in the opposite direction. Hence the flow rate is negative and the same equations obtained.
\[
\label{if:eq:sinkePotential}
\phi - \phi_0 = -\dfrac{\dot{Q}}{ 2\,\pi\,r}\, \ln \dfrac{r}{r_0}
\]
\[
\label{if:eq:sinkStream}
\psi - \psi_0 = -\dfrac{\dot{Q}}{ 2\,\pi\,r}\, \left( \theta -\theta_0\right)
\]
Free Vortex Flow
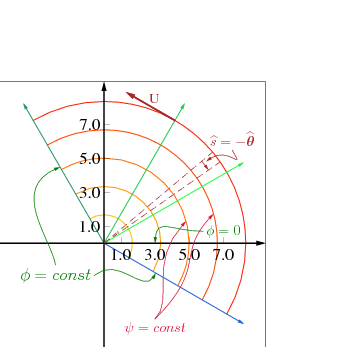
Fig. 10.8 Two dimensional Vortex free flow. In the diagram exhibits part the circle to explain the stream lines and potential lines.
As opposed to the radial flow direction (which was discussed under the source and sink) the flow in the tangential direction is referred to as the free vortex flow. Another typical name for this kind of flow is the potential vortex flow. The flow is circulating the origin or another point. The velocity is only a function of the distance from the radius as
\[
\label{if:eq:Uvortisity}
U_{\theta} = f(r)
\]
\[
\label{if:eq:UvecVortisity}
\mathbf{U} = \widehat{\boldsymbol{\theta}}\, f(r)
\]
The fundamental aspect of the potential flow is that this flow must be irrotational flow. The gradient of the potential in cylindrical coordinates is
\[
\label{if:eq:gradientCyl}
\mathbf{U} = \boldsymbol{\nabla}\phi = \dfrac{\partial \phi}{\partial r}\, \widehat{\mathbf{r}} +
\dfrac{1}{r}\,\dfrac{\partial \phi}{\partial \theta} \,\widehat{\mathbf{\theta}}
\]
Hence, equation (20) dictates that
\[
\label{if:eq:vortisityODE}
\begin{array}{rl}
\dfrac{1}{r}\,\dfrac{\partial \phi}{\partial \theta} = f(r) \\
\dfrac{\partial \phi}{\partial r} = 0
\end{array}
\]
From these equations it can be seem that
\[
\label{if:eq:vertisityODEsol1}
\phi = \phi (\theta)
\]
and
\[
\label{if:eq:vertisityODE2}
\dfrac{\partial \phi}{\partial \theta} = r \,f(r)
\]
Equation (23) states that the potential function depends on the angle, \(\theta\) while it also a function of the radius. The only what the above requirement is obtained when the derivative of \(\phi\) and the equation are equal to a constant. Thus,
\[
\label{if:eq:vertisityODE2sol}
\begin{array}{rl}
r \,f(r) = c \Longrightarrow f(r) = \dfrac{c}{r} \\
\dfrac{\partial \phi}{\partial \theta} = c \Longrightarrow \phi-\phi_0 = c_1\, ( 0 - \theta_0)
\end{array}
\]
It can be observed from equation (23) that the velocity varies inversely with the radius. This variation is referred in the literature as the natural vortex as oppose to forced vortex where the velocity varies in any different functionality. It has to be noted that forced vortex flow is not potential flow. The stream function can be found in the "standard'' way as
\[
\nonumber
d\psi = \mathbf{U} \,\mathbf{\cdot} \, \widehat{s} \,dr
\]
It can observed, in this case, from Figure 10.8 that \(\widehat{s}= -\widehat{\mathbf{\theta}}\) hence
\[
\label{if:eq:vortexPotentialD}
d\psi = \widehat{\mathbf{\theta}} \, \dfrac{c_1}{r} \,\mathbf{\cdot} \,(-\widehat{\mathbf{\theta}}) \,dr
= c_1 \dfrac{dr}{r}
\]
Thus,
\[
\label{if:eq:vortexPotential}
\psi - \psi_0 = -c_1\, \ln \left( \dfrac{r}{r_0} \right)
\]
The source point or the origin of the source is a singular point of the stream function and there it cannot be properly defined. Equation (24) dictates that velocity at the origin is infinity. This similar to natural situation such as tornadoes, hurricanes, and whirlpools where the velocity approaches a very large value near the core. In these situation the pressure became very low as the velocity increase. Since the pressure cannot attain negative value or even approach zero value, the physical situation changes. At the core of these phenomenon a relative zone calm zone is obtained.
The Circulation Concept
In the construction of the potential flow or the inviscid flow researchers discover important concept of circulation. This term mathematically defined as a close path integral around area (in two dimensional flow) of the velocity along the path. The circulation is denoted as \(\Gamma\) and defined as
\[
\label{if:eq:circulation}
\Gamma = \oint \mathbf{U}_s\, ds
\]
Where the velocity \(\mathbf{U}_s\) represents the velocity component in the direction of the path. The symbol \(\oint\) indicating that the integral in over a close path.
Fig. 10.9 Circulation path to illustrate varies calculations.
Mathematically to obtain the integral the velocity component in the direction of the path has to be chosen and it can be defined as
\[
\label{if:eq:Circulation}
\Gamma = \oint_C \mathbf{U} \, \mathbf{\cdot}\, \widehat{\mathbf{ds}}
\]
\[
\label{if:eq:CirculationPotential}
\Gamma = \oint_C \mathbf{\nabla}\phi \, \mathbf{\cdot}\, \overbrace{\widehat{\mathbf{s}} \,ds}^{\widehat{\mathbf{ds}}}
\]
And using some mathematical manipulations yields
\[
\label{if:eq:cpManipulation}
\Gamma = \oint_C \overbrace{\dfrac{d\phi}{ds} }^
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/10:_Inviscid_Flow_or_Potential_Flow/10.3_Potential_Flow_Functions_Inventory), /content/body/div[4]/p[9]/span, line 1, column 1
= \oint_C d\phi
\] The integration of equation (31) results in
\[
\label{if:eq:cpManipulationR1}
\Gamma = \oint_C d\phi = \phi_2 (\text{starting point}) - \phi_1 (\text{starting point})
\]
Unless the potential function is dual or multi value, the difference between the two points is zero. In fact this what is expected from the close path integral. However, in a free vortex situation the situation is different. The integral in that case is the integral around a circular path which is
\[
\label{if:eq:circulationFreeVortex}
\Gamma = \oint \mathbf{U} \,\mathbf{\cdot}\, \mathbf{i} \, \overbrace{r \,d\theta}{ds} =
\oint \dfrac{c_1}{r} \,r\,d\theta
= c_1\,2\,\pi
\]
In this case the circulation, \(\Gamma\) is not vanishing. In this example, the potential function \(\phi\) is a multiple value as potential function the potential function with a single value.
Example 10.5
Calculate the circulation of the source on the path of the circle around the origin with radius \(a\) for a source of a given strength.
Solution 10.5
The circulation can be carried by the integration
\[
\label{circulationSource:fromDef}
\Gamma = \oint \overbrace{\mathbf{U} \,\mathbf{\cdot}\, \mathbf{i}}^{=0} \, r \,d\theta\,{ds} = 0
\]
Thus, there are two kinds of potential functions one where there are single value and those with multi value. The free vortex is the cases where the circulation add the value of the potential function every rotation. Hence, it can be concluded that the potential function of vortex is multi value which increases by the same amount every time, \(c_1\,2\,\pi\). In this case value at \(\theta=0\) is different because the potential function did not circulate or encompass a singular point. In the other cases, every additional enclosing adds to the value of potential function a value.
It was found that the circulation, \(\Gamma\) is zero when there is no singular point within the region inside the path.
For the free vortex the integration constant can be found if the circulation is known as
\[
\label{if:eq:ConstatntVortext}
c_1 = \dfrac{\Gamma}{2\,\pi}
\]
In the literature, the term \(\Gamma\) is, some times, referred to as the "strength'' of the vortex. The common form of the stream function and potential function is in the form of
\[
\label{if:eq:typicalPhiVortex}
\phi = \dfrac{\Gamma}{2\,\pi} \left(\theta -\theta_0\right) + \phi_0
\]
\[
\label{if:eq:typicalPsiVortex}
\psi = \dfrac{\Gamma}{2\,\pi} \ln\left( \dfrac{r}{r_0}\right) + \psi_0
\]
Superposition of Flows
For incompressible flow and two dimensional the continuity equation reads
\[
\label{if:eq:Laplaces}
\mathbf{\nabla} \mathbf{\cdot} \mathbf{U} =
\mathbf{\nabla} \mathbf{\cdot} \mathbf{\nabla} \phi =
\mathbf{\nabla}^2 \phi =
\dfrac{\partial^2\phi}{\partial x^2} + \dfrac{\partial^2\phi}{\partial y^2} = 0
\]
The potential function must satisfy the Laplace's equation which is a linear partial differential equation. The velocity perpendicular to a solid boundary must be zero (boundary must be solid) and hence it dictates the boundary conditions on the potential equation. From mathematical point of view this boundary condition as
\[
\label{if:eq:bcSolid}
\mathbf{U}_n = \dfrac{d\phi}{dn} = \mathbf{\nabla}{\phi}\mathbf{\cdot} \widehat{\mathbf{n}} = 0
\]
\[
\label{if:eq:laplacianSuperposition}
\overbrace{\mathbf{\nabla}^2\phi_1}^{=0} + \overbrace{\mathbf{\nabla}^2\phi_2}^{=0} = 0
\]
Since the Laplace mathematical operator is linear the two potential can be combined as
\[
\label{if:eq:laplacianSuperpositionCombined}
\mathbf{\nabla}^2\left(\phi_1 + \phi_2\right) = 0
\]
The boundary conditions can be also treated in the same fashion. On a solid boundary condition for both functions is zero hence
\[
\label{if:eq:laplacianSuperpositionBC1}
\dfrac{d\phi_1}{dn} = \dfrac{d\phi_2}{dn} = 0
\]
and the normal derivative is linear operator and thus
\[
\label{if:eq:laplacianSuperpositionBC2}
\dfrac{d\left(\phi_1+ \phi_2\right)}{dn} = 0
\]
It can be observed that the combined new potential function create a new velocity field. In fact it can be written that
\[
\label{if:eq:combinedU}
\mathbf{U} = \mathbf{\nabla} (\phi_1+\phi_2) = \mathbf{\nabla} \phi_1+ \mathbf{\nabla} \phi_2 =
\mathbf{U}_1 + \mathbf{U}_2
\]
The velocities \(\mathbf{U}_1\) and \(\mathbf{U}_2\) are obtained from \(\phi_1\) and \(\phi_2\) respectively. Hence, the superposition of the solutions is the characteristic of the potential flow.
Source and Sink Flow or Doublet Flow
In the potential flow, there is a special case where the source and sink are combined since it represents a special and useful shape. A source is located at point B which is \(r_0\) from the origin on the positive \(x\) coordinate. The flow rate from the source is \(Q_0\) and the potential function is
\[
\label{if:eq:doublet:sourcePF}
Q_1 = \dfrac{Q_0}{2\,\pi} \ln \left( \dfrac {r_B}{r_0}\right)
\]
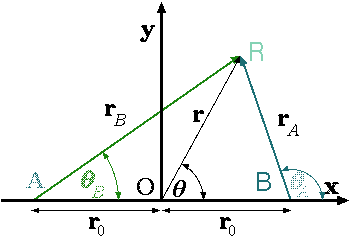
Fig. 10.10 Combination of the Source and Sink located at a distance \(r_0\) from the origin on the \(x\) coordinate. The source is on the right.
The sink is at the same distance but at the negative side of the\(x\) coordinate and hence it can be represented by the potential function
\[
\label{if:eq:doublet:sinkPF}
Q_1 = -\dfrac{Q_0}{2\,\pi} \ln \left( \dfrac {r_A}{r_0}\right)
\]
The description is depicted on Figure 10.10. The distances, \(r_A\) and \(r_B\) are defined from the points \(A\) and \(B\) respectively. The potential of the source and the sink is
\[
\label{if:eq:doubletPotential}
\phi = \dfrac{Q_0}{2\,\pi} \, \left( \ln r_A - \ln r_B\right)
\]
\[
\label{if:eq:cosinesLawR}
{r_B}^2 = r^2 + {r_0}^2 - 2\,r\,r_0\,cos\theta
\]
In the same manner it applied to the left triangle as
\[
\label{if:eq:cosinesLawL}
{r_A}^2 = r^2 + {r_0}^2 + 2\,r\,r_0\,cos\theta
\]
Therefore, equation (47) can be written as
\[
\label{if:eq:cosinesLawCombine}
\phi = - \dfrac{Q_0}{2\,\pi} \, \dfrac{1}{2} \, \ln \left(
\dfrac{\dfrac{r^2+{r_0}^2}{2\,r\,r_0\, \cos \theta} + 1}
{\dfrac{r^2+{r_0}^2}{2\,r\,r_0\, \cos \theta} - 1}\right)
\]
It can be shown that the following the identity exist
Caution: mathematical details which can be skipped
\[
\label{if:eq:mathIdenty}
\coth^{-1} (\xi) = \dfrac{1}{2} \ln \left( \dfrac{\xi + 1 }{ \xi - 1} \right)
\]
\[
\label{if:eq:doubletPotentialFc}
\phi = - \dfrac{Q_0}{2\,\pi} \, \coth^{-1} \left( \dfrac{r^2+{r_0}^2}{2\,r\,r_0\, \cos \theta}\right)
\]
The several following stages are more of a mathematical nature which provide minimal contribution to physical understanding but are provide to interested reader. The manipulations are easier with an implicit solution and thus
\[
\label{if:eq:doubletImpliciteIni}
\coth \left( - \dfrac{2\,\pi\,\phi}{Q}\right) = \dfrac{r^2+{r_0}^2}{2\,r\,r_0\, \cos \theta}
\]
Equation (53), when noticing that the \(\,\cos\theta\, \coth(-x) = - \coth(x)\), can be written as
\[
\label{if:eq:doubletImpliciteInif}
-2\,r_0\,r\,\cos\theta\coth \left( \dfrac{2\,\pi\,\phi}{Q}\right)
= {r^2+{r_0}^2}
\]
In Cartesian coordinates equation (54) can be written as
\[
\label{if:eq:doubletImpliciteInic}
-2\,r_0\,\overbrace{x}^{r\,\cos\theta}\,
\coth \left( - \dfrac{2\,\pi\,\phi}{Q}\right) = {x^2+y^2 +{r_0}^2}
\]
Equation (55) can be rearranged by the left hand side to right as and moving \({r_0}^2\) to left side result in
\[
\label{if:eq:doubletImpliciteInic1}
- {r_0}^2 = 2\,r_0\,\overbrace{x}^{r\,\cos\theta}\,
\coth \left( \dfrac{2\,\pi\,\phi}{Q}\right) + x^2+y^2
\]
Add to both sides \({r_0}^2\,\coth^2\dfrac{2\,\pi\,\phi}{Q_0}\) transfers equation (??)
\[
\label{if:eq:doubletImpliciteInic2a}
{r_0}^2\,\coth^2\dfrac{2\,\pi\,\phi}{Q_0} - {r_0}^2 =
{r_0}^2\,\coth^2\dfrac{2\,\pi\,\phi}{Q_0} + 2\,r_0\,\overbrace{x}^{r\,\cos\theta}\,
\coth \left( \dfrac{2\,\pi\,\phi}{Q}\right) + x^2+y^2
\]
The hyperbolic identity can be written as
\[
\label{if:eq:doubletImpliciteInic2}
{r_0}^2\,\text{csch}^2\dfrac{2\,\pi\,\phi}{Q_0} =
{r_0}^2\,\coth^2\dfrac{2\,\pi\,\phi}{Q_0} + 2\,r_0\,\overbrace{x}^{r\,\cos\theta}\,
\coth \left( \dfrac{2\,\pi\,\phi}{Q}\right) + x^2+y^2
\]
End Caution: mathematical details
It can be noticed that first three term on the right hand side are actually quadratic and can be written as
\[
\label{if:eq:doubletImpliciteInic3}
{r_0}^2\,\text{csch}^2\dfrac{2\,\pi\,\phi}{Q_0} =
\left( {r_0}\,\coth\dfrac{2\,\pi\,\phi}{Q_0} + x \right)^2 + y^2
\]
equation (59) represents a circle with a radius \({r_0}\,\text{csch}\dfrac{2\,\pi\,\phi}{Q_0}\) and a center at \(\pm r_0\coth \left( \dfrac{2\,\pi \, \phi}{Q_0} \right)\). The potential lines depicted on Figure 10.11. For the drawing purposes equation (59) is transformed into a dimensionless form as
\[
\label{if:eq:doubletImpliciteInicDlss}
\left( \coth\dfrac{2\,\pi\,\phi}{Q_0} + \dfrac{x}{r_0} \right)^2 + \left(\dfrac{y}{r_0}\right)^2
= \text{csch}^2\dfrac{2\,\pi\,\phi}{Q_0}
\]
Fig. 10.11 Stream and Potential line for a source and sink. It can be noticed that stream line (in blue to green) and the potential line are in orange to crimson. This figure is relative distances of \(x/r_0\) and \(y/r_0\). The parameter that change is \(2\,\pi\,\phi/Q_0\) and \(2\,\pi\,\psi/Q_0\). Notice that for give larger of \(\phi\) the circles are smaller.
The stream lines can be obtained by utilizing similar procedure. The double stream function is made from the combination of the source and sink because stream functions can be added up. Hence,
\[
\label{if:eq:doubleStream}
\psi = \psi_1 + \psi_2 = \dfrac{Q_0}{2\,\pi} \left( \theta_1 - \theta_2\right)
\]
The angle \(\theta_1\) and \(\theta_2\) shown in Figure 10.11 related other geometrical parameters as
\[
\label{if:eq:doubletAngle1}
\theta_1 = \tan^{-1} \dfrac{y}{x-r_0}
\]
\[
\label{if:eq:doubletAngle2}
\theta_2 = \tan^{-1} \dfrac{y}{x+r_0}
\]
The stream function becomes
\[
\label{if:eq:doubletStreamIni}
\psi = \dfrac{Q_0}{2\,\pi} \left( \tan^{-1} \dfrac{y}{x-r_0} - \tan^{-1} \dfrac{y}{x+r_0} \right)
\]
Caution: mathematical details which can be skipped
Rearranging equation (64) yields
\[
\label{if:eq:doubletStreamIntermid}
\dfrac{2\,\pi\,\psi}{Q_0} =
\tan^{-1} \dfrac{y}{x-r_0} - \tan^{-1} \dfrac{y}{x+r_0}
\]
\[
\label{if:eq:doubletStreamIntermidT}
\tan \dfrac{2\,\pi\,\psi}{Q_0} =
\dfrac{\dfrac{y}{x-r_0} - \dfrac{y}{x+r_0}}
{1 + \dfrac{y^2}{x^2-{r_0}^2}}
\]
As in the potential function cases, Several manipulations to convert the equation (66) form so it can be represented in a "standard'' geometrical shapes are done before to potential function. Reversing and finding the common denominator provide
\[
\label{if:eq:doubletStreamIntermidRev}
\cot \dfrac{2\,\pi\,\psi}{Q_0} =
\dfrac { \dfrac{ x^2-{r_0}^2 + y^2 }{x^2-{r_0}^2} } {\dfrac{y\, (x+r_0) - y\,(x-r_0) }{x^2 - {r_0}^2} }
= \dfrac{ x^2-{r_0}^2 + y^2 }{\underbrace{y\, (x+r_0) + y\,(x-r_0) }_{2\,y\,r_0 } }
\]
or
\[
\label{if:eq:doubletStreamIntermidRev1}
x^2+ y^2-{r_0}^2 = 2\, r_0 \, y \cot \dfrac{2\,\pi\,\psi}{Q_0}
\]
End Caution: mathematical details
Equation (68) can be rearranged, into a typical circular representation
\[
\label{if:eq:doubleStreamF1}
x^2 +\left( y - r_0\cot\dfrac{2\,\pi\,\psi}{Q_0}\right)^2 =
\left( r_0\csc\dfrac{2\,\pi\,\psi}{Q_0} \right)^2
\]
\[
\label{if:eq:doubleStreamF2}
\left( \dfrac{x}{r_0}\right)^2 +\left( \dfrac{y} {r_0} - \cot\dfrac{2\,\pi\,\psi}{Q_0}\right)^2 =
\left( \csc\dfrac{2\,\pi\,\psi}{Q_0} \right)^2
\]
Dipole Flow
It was found that when the distance between the sink and source shrinks to zero a new possibility is created which provides benefits to new understanding. The new combination is referred to as the dipole. Even though, the construction of source/sink to a single location (as the radius is reduced to zero) the new "creature'' has direction as opposed to the scalar characteristics of source and sink. First the potential function and stream function will be presented. The potential function is
\[
\label{if:eq:doubleImitIni}
\lim_{r_0\rightarrow 0}\phi = - \dfrac{Q_0}{2\,\pi} \, \dfrac{1}{2}\,\ln \left(
\dfrac{r^2+{r_0}^2 - 2\,r\,r_0\, \cos \theta}
{r^2+{r_0}^2 + 2\,r\,r_0\, \cos \theta }\right)
\]
To determine the value of the quantity in equation (71) the L'Hôpital's rule will be used. First the appropriate form will be derived so the technique can be used.
Caution: mathematical details which can be skipped
Multiplying and dividing equation (71) by \(2\,r_0\) yields
\[
\label{if:eq:doubleImit1}
\lim_{r_0\rightarrow 0}\phi = \overbrace{\dfrac{Q_0\,2\,r_0}{2\,\pi}}
^{{ 1^{st}\, part} }
\, \overbrace{\dfrac{1}{\underbrace{2\,\,2}_{4}\,r_0}
\,\ln \left(
\dfrac{r^2+{r_0}^2 - 2\,r\,r_0\, \cos \theta}
{r^2+{r_0}^2 + 2\,r\,r_0\, \cos \theta }\right) }^{\mathrm 2^{nd} \, part}
\]
\[
\label{if:eq:doubleImit2}
\lim_{r_0\rightarrow 0} \dfrac{
\ln \left(
\dfrac{r^2+{r_0}^2 - 2\,r\,r_0\, \cos \theta}
{r^2+{r_0}^2 + 2\,r\,r_0\, \cos \theta }\right)
}{4\,r_0}
\]
It can be noticed that the ratio in the natural logarithm approach one \(r_0\rightarrow 0\). The L'Hopital's rule can be applied because the situation of nature of \(0/0\). The numerator can be found using a short cut
End Caution: mathematical details
at
\[
\label{if:eq:doubleImit2Lhopital}
\lim_{r_0\rightarrow 0} \dfrac{ \dfrac{\cancelto{0}{2\,r_0} - 2\,r\,\cos\theta}
{r^2+\cancelto{0}
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/10:_Inviscid_Flow_or_Potential_Flow/10.3_Potential_Flow_Functions_Inventory), /content/body/div[7]/p[11]/span, line 1, column 4
{4} = - \dfrac{\cos\theta}{r}
\]
Combining the first and part with the second part results in
\[
\label{if:eq:doubleImitF1}
\phi = - \dfrac{Q_0\,r_0}{\pi} \dfrac{\cos\theta}{r}
\]
After the potential function was established the attention can be turned into the stream function. To establish the stream function, the continuity equation in cylindrical is used which is
\[
\nonumber
\mathbf{\nabla} \mathbf{\cdot} \mathbf{U} = \dfrac{1}{r}
\left( \dfrac{\partial \,r\,U_r}{\partial r} + \dfrac{\partial \,U_{\theta}}{\partial \theta} \right)
\]
The transformation of equations (??) and (??) to cylindrical coordinates results in
\[
\label{if:eq:streamFunCylindricalR}
U_r = \dfrac{1}{r} \dfrac{\partial \psi}{\partial \theta}
\]
\[
\label{if:eq:streamFunCylindricalTheta}
U_{\theta} = - \dfrac{\partial \psi}{\partial r}
\]
The relationship for the potential function of the cylindrical coordinates was determined before an appear the relationship (??) and (??)
\[
\label{if:eq:potentionalUCylindricalIni}
U_r = \dfrac{\partial \phi}{\partial r} \quad \text{and} \quad
\]
\[
\label{if:eq:potentionalUCylindrical}
U_{\theta} = \dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta}
\]
Thus the relationships that were obtained before for Cartesian coordinates is written in cylindrical coordinates as
\[
\label{if:eq:psUrCylindrical}
\dfrac{\partial \phi}{\partial r} = \dfrac{1}{r} \dfrac{\partial \psi}{\partial \theta}
\]
\[
\label{if:eq:psUthetaCylindrical}
\dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta} = - \dfrac{\partial \psi}{\partial r}
\]
In the case of the dipole, the knowledge of the potential function is used to obtain the stream function. The derivative of the potential function as respect to the radius is
\[
\label{if:eq:doublePdr}
\dfrac{\partial \phi}{\partial r} = \dfrac{Q_0}{2\,\pi} \,\dfrac{\cos\theta}{r^2}
\dfrac{1}{r} \dfrac{\partial \psi}{\partial \theta}
\]
\[
\label{if:eq:doubleSdr}
\dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta} = \dfrac{Q_0}{2\,\pi} \,\dfrac{\sin\theta}{r^2}
- \dfrac{\partial \psi}{\partial r}
\]
From equation (83) after integration with respect to \(\theta\) one can obtain
\[
\label{if:eq:doublePdrSol}
\psi = \dfrac{Q_0}{2\,\pi\,r} \, \sin \theta + f(r)
\]
\[
\label{if:eq:doubleDdrSol}
- \dfrac{\partial \psi}{\partial r} = \dfrac{Q_0}{2\,\pi\,r^2} \sin\theta + f'(r)
\]
The only way that these conditions co–exist is \(f(r)\) to be constant and thus \(f'(r)\) is zero. The general solution of the stream function is then
\[
\label{if:eq:doubleStreamF}
\psi = \dfrac{Q_0\,\sin\theta}{2\,\pi\,r}
\]
Caution: mathematical details which can be skipped
The potential function and stream function describe the circles as following: In equation (87) it can be recognized that \(r= \sqrt{x^2+y^2}\) Thus, multiply equation (87) by \(r\) and some rearrangement yield
\[
\label{if:eq:psiCircule1}
\dfrac{2\,\pi\,\psi}{Q_0}\,\left(\overbrace{x^2+y^2}^{r^2}\right) = \overbrace{y}^{r\,sin\theta}
\]
\[
\label{if:eq:psiCircule2}
\left(\overbrace{x^2+y^2}^{r^2}\right) = \dfrac{Q_0}{2\,\pi\,\psi}\, \overbrace{y}^{r\,\sin\theta}
- \overbrace{
\left( \dfrac{Q_0}{2\,\pi\,\psi} \right)^2 + \left( \dfrac{Q_0}{2\,\pi\,\psi} \right)^2 } ^{=0}
\]
and converting to the standard equation of circles as
\[
\label{if:eq:psiCircule3}
\overbrace{
y^2 - \dfrac{Q_0}{2\,\pi\,\psi}\,y + \left( \dfrac{Q_0}{2\,\pi\,\psi} \right)^2}^{y-
\dfrac{Q_0}{2\,\pi\,\psi}} + \,x^2 = \left(\dfrac{Q_0}{2\,\pi\,\psi} \right)^2
\]
End Caution: mathematical details
The equation (87) (or (90) represents a circle with a radius of \(\dfrac{Q_0}{2\,\pi\,\psi}\) with location at \(x=0\) and \(y=\pm\dfrac{Q_0}{2\,\pi\,\psi}\). The identical derivations can be done for the potential function. It can be noticed that the difference between the functions results from difference of \(r\sin\theta\) the instead of the term is \(r\cos\theta\). Thus, the potential functions are made from circles that the centers are at same distance as their radius from origin on the \(x\) coordinate. It can be noticed that the stream function and the potential function can have positive and negative values and hence there are family on both sides of coordinates. Figure 10.12 displays the stream functions (cyan to green color) and potential functions (gold to crimson color). Notice the larger the value of the stream function the smaller the circle and the same for the potential functions.
Fig. 10.12 Stream lines and Potential lines for Doublet. The potential lines are in gold color to crimson while the stream lines are cyan to green color. Notice the smaller value of the stream function translates the smaller circle. The drawing were made for the constant to be one (1) and direct value can be obtained by simply multiplying.
It must be noted that in the derivations above it was assumed that the sink is on the left and source is on the right. Clear similar results will obtained if the sink and source were oriented differently. Hence the dipole (even though) potential and stream functions are scalar functions have a direction. In this stage this topic will not be treated but must be kept in question form.
Example 10.6
This academic example is provided mostly for practice of the mathematics. Built the stream function of dipole with angle. Start with a source and a sink distance \(r\) from origin on the line with a angle \(\beta\) from \(x\) coordinates. Let the distance shrink to zero. Write the stream function.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.
2πψQ0=tan−1y
x/


