1.2: Flow Regimes Literature

Based on the specific gravity of particles with a magnitude of 2.65, Durand (1953) proposed to divide the flows of non-settling slurries in horizontal pipes into four flow regimes based on average particle size as follows:

1. Homogeneous suspensions for particles smaller than 40 \(\ \mathrm {\mu} \mathrm{m}\) (mesh 325)
2. Suspensions maintained by turbulence fro particle sizes from 40 \(\ \mathrm {\mu} \mathrm{m}\) (mesh 325) to 0.15 mm (mesh 100)
3. Suspension with saltation fro particle sizes between 0.15 mm (mesh 100) and 1.5 mm (mesh 11)
4. Saltation for particles greater than 1.5 mm (mesh 11)

Due to the interrelation between particle sizes and terminal and deposition velocities, the original classification proposed by Durand has been modified to four flow regimes based on the actual flow of particles and their size (Abulnaga, 2002).

1. Flow with a stationary bed
2. Flow with a moving bed and saltation (with or without suspension)
3. Heterogeneous
   • Heterogeneous mixture with saltation and rolling
   • Heterogeneous mixture with all solids in suspension
4. Pseudo homogeneous and/or homogeneous mixtures with all solids in suspension

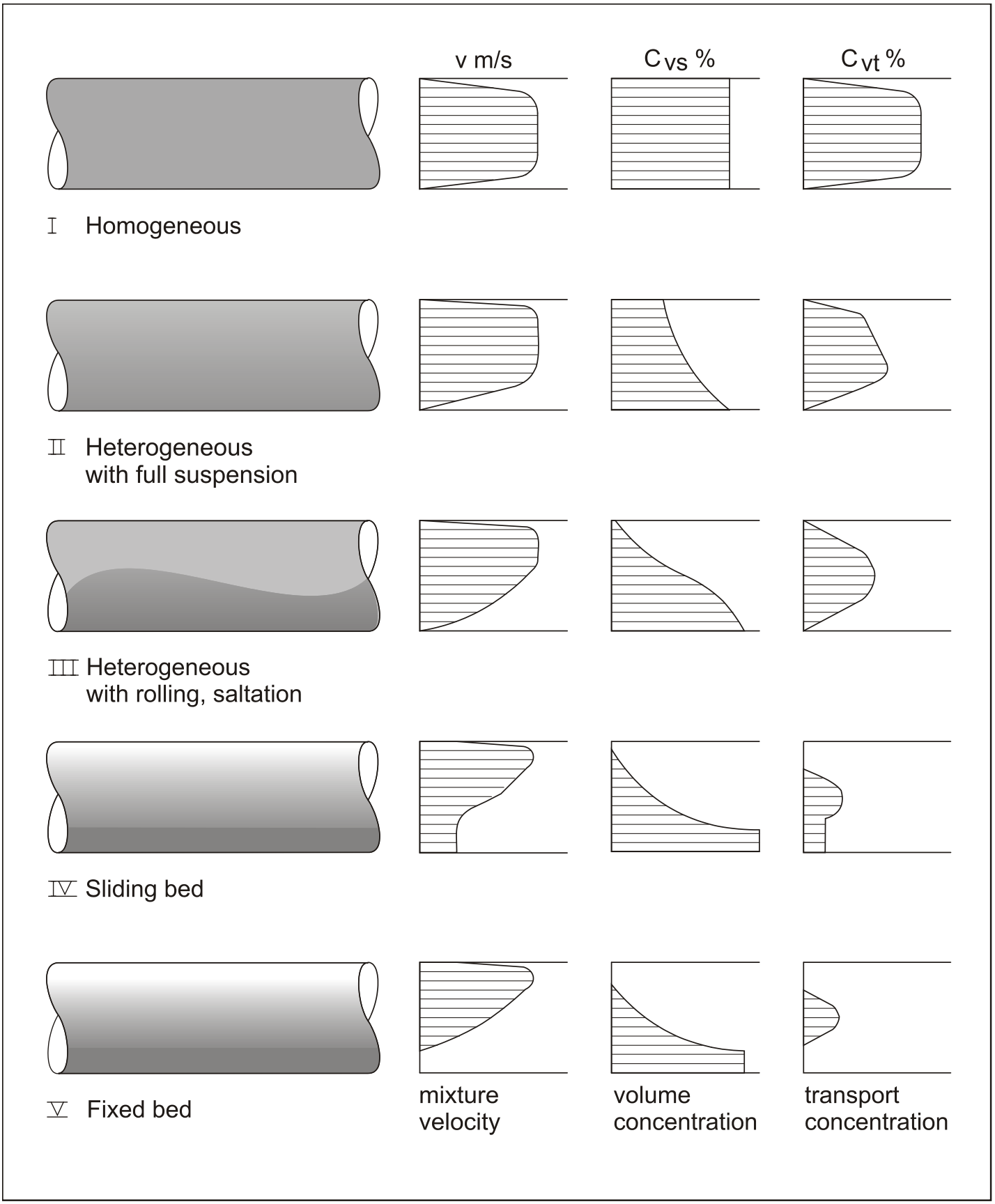
The four regimes of flow can be represented by a plot of the hydraulic gradient versus the average speed of the mixture as in Figure 1.2-1. The 4 transitional velocities are defined as:

• V₁: velocity at or above which the bed in the lower half of the pipe is stationary. In the upper half of the pipe, some solids may move by saltation or suspension. Below V1 there are no particles above the bed.
• V₂: velocity at or above which the mixture flows as an asymmetric mixture with the coarser particles forming a moving/saltating bed.
• V₃: velocity at or above which all particles move as an asymmetric suspension and below which the solids start to settle and form a moving bed.
• V₄: velocity at or above which all solids move as an almosrt symetric syspension

Wilson (1992) developed a model, which will be discussed in detail later, for the incipient motion of granular solids at V₂, the transition between a stationary bed and a sliding bed. He assumed a hydrostatic pressure exerted by the solids on the wall. Wilson also developed a model for heterogeneous transport with a V₅₀, where 50% of the solids are in a (moving/saltating) bed and 50% in suspension. This percentage is named the stratification ratio. The transitional velocity V₃ is extremely important because it is the speed at which the hydraulic gradient is at a minimum. Although there is evidence that solids start to settle at lower line speeds in complex mixtures, operators and engineers often refer to this transitional velocity as the speed of deposition or critical velocity. Figure 1.2-3 shows the 4 regimes and the velocity and concentration profiles. At very high line speeds the pressure drop will reach an equivalent liquid curve asymptotically. Whether or not this occurs at practical line speeds depends on the particle diameter, pipe diameter and the concentration. For large particle diameters and concentrations it may seem like the pressure drop reaches the water curve asymptotically, but at higher line speeds the pressure drop will increase again up to an equivalent liquid model. Whether or not this equivalent liquid model contains the mixture density instead of the water density, or some value in between is still the question.

Figure 1.2-1: The 4 regimes and transitional velocities (Abulnaga, 2002), Dp=0.15 m, d50=2 mm, Cvt=0.2.

Figure 1.2-1 gives the impression that the 4 flow regimes will always occur sequentially. Starting from a line speed zero and increasing the line speed, first the fixed or stationary bed will occur without suspension, at a line speed V1 part of the bed starts to erode and particles will be in suspension, at a line speed V2 the remaining bed will start to slide while the erosion increases with the line speed, at a line speed V3 the whole bed is eroded and the heterogeneous regime starts and finally at a line speed V4 the heterogeneous regime transits to the (pseudo) homogeneous regime. In reality not all the regimes have to occur, depending on the particle size, the pipe diameter and other governing parameters.

Figure 1.2-2: Flow regimes according to Newitt et al. (1955).

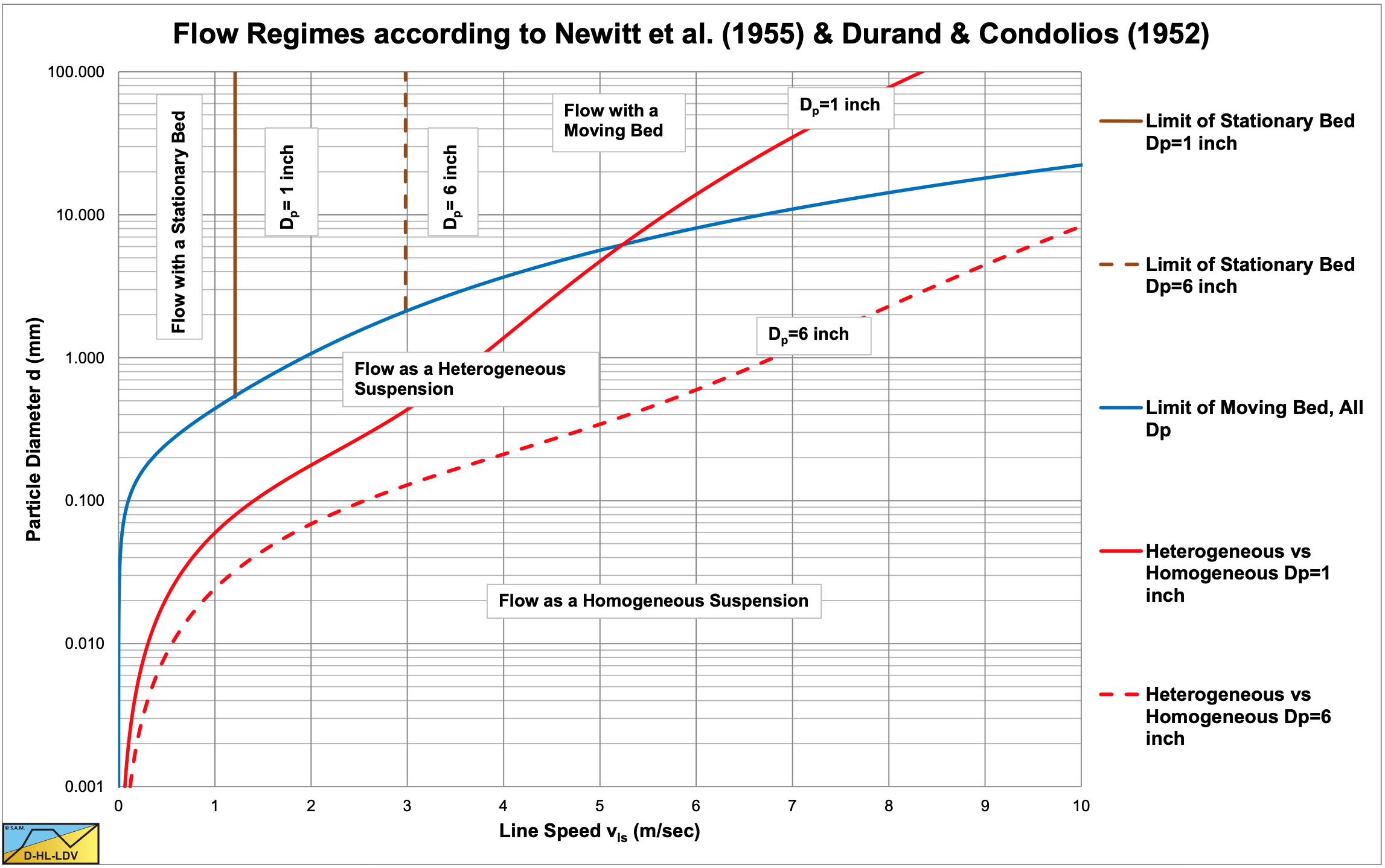
Figure 1.2-2 shows the regimes according to Newitt et al. (1955). From this figure it is clear that not all regimes have to occur and that the transition velocities depend on the particle and the pipe diameter. The influence of the volumetric concentration is not present in this graph. Figure 1.2-3 shows the flow regimes as used by Matousek (2004) also showing velocity and concentration distributions.

Figure 1.2-3: Different mixture transport regimes.