3.2: The Darcy-Weisbach Friction Factor
- Page ID
- 29284
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The value of the wall friction factor \(\ \mathrm{\lambda_{l}}\) depends on the Reynolds number:
\[\ \mathrm{R} \mathrm{e}=\frac{\mathrm{v}_{\mathrm{l s}} \cdot \mathrm{D}_{\mathrm{p}}}{v_{\mathrm{l}}}=\frac{\rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}} \cdot \mathrm{D}_{\mathrm{p}}}{\mu_{\mathrm{l}}}\]
For laminar flow (\(Re<2320\)) the value of \(\ \lambda_{l}\) can be determined according to Poiseuille:
\[\ \lambda_{1}=\frac{64}{\mathrm{Re}}\]
For turbulent flow (\(Re>2320\)) the value of \(\ \mathrm{\lambda_{l}}\) depends not only on the Reynolds number but also on the relative roughness of the pipe \(\ \mathrm{\varepsilon}\)/Dp, which is the absolute roughness \(\ \mathrm{\varepsilon}\) divided by the pipe diameter Dp. A general implicit equation for \(\ \mathrm{\lambda_{l}}\) is the Colebrook-White (1937) equation:
\[\ \lambda_{1}=\frac{1}{\left(2 \cdot \log _{10}\left(\frac{2.51}{\operatorname{Re} \cdot \sqrt{\lambda_{1}}}+\frac{0.27 \cdot \varepsilon}{D_{p}}\right)\right)^{2}}\]
For very smooth pipes the value of the relative roughness \(\ \mathrm{\varepsilon}\)/Dp is almost zero, resulting in the Prandl & von Karman equation:
\[\ \lambda_{1}=\frac{1}{\left(2 \cdot \log _{10}\left(\frac{2.51}{\operatorname{Re} \cdot \sqrt{\lambda_{1}}}\right)\right)^{2}}\]
At very high Reynolds numbers the value of \(\ 2.51 /(\mathrm{Re} \cdot \sqrt{\lambda_{1}})\) is almost zero, resulting in the Nikuradse (1933) equation:
\[\ \lambda_{1}=\frac{1}{\left(2 \cdot \log _{10}\left(\frac{0.27 \cdot \varepsilon}{D_{p}}\right)\right)^{2}}=\frac{5.3}{\left(2 \cdot \ln \left(\frac{0.27 \cdot \varepsilon}{D_{p}}\right)\right)^{2}}\]
Because equations (3.2-3) and (3.2-4) are implicit, for smooth pipes approximation equations can be used. For a Reynolds number between 2320 and 105 the Blasius equation gives a good approximation:
\[\ \lambda_{1}=0.3164 \cdot\left(\frac{1}{R e}\right)^{0.25}\]
For a Reynolds number in the range of 105 to 108 the Nikuradse (1933) equation gives a good approximation:
\[\ \lambda_{\mathrm{l}}=\mathrm{0 . 0 0 3 2}+\frac{\mathrm{0 . 2 2 1}}{\mathrm{R e}^{\mathrm{0 . 2 3 7}}}\]
Figure 3.2-1 gives the so called Moody (1944) diagram, in this case based on the Swamee Jain (1976) equation.
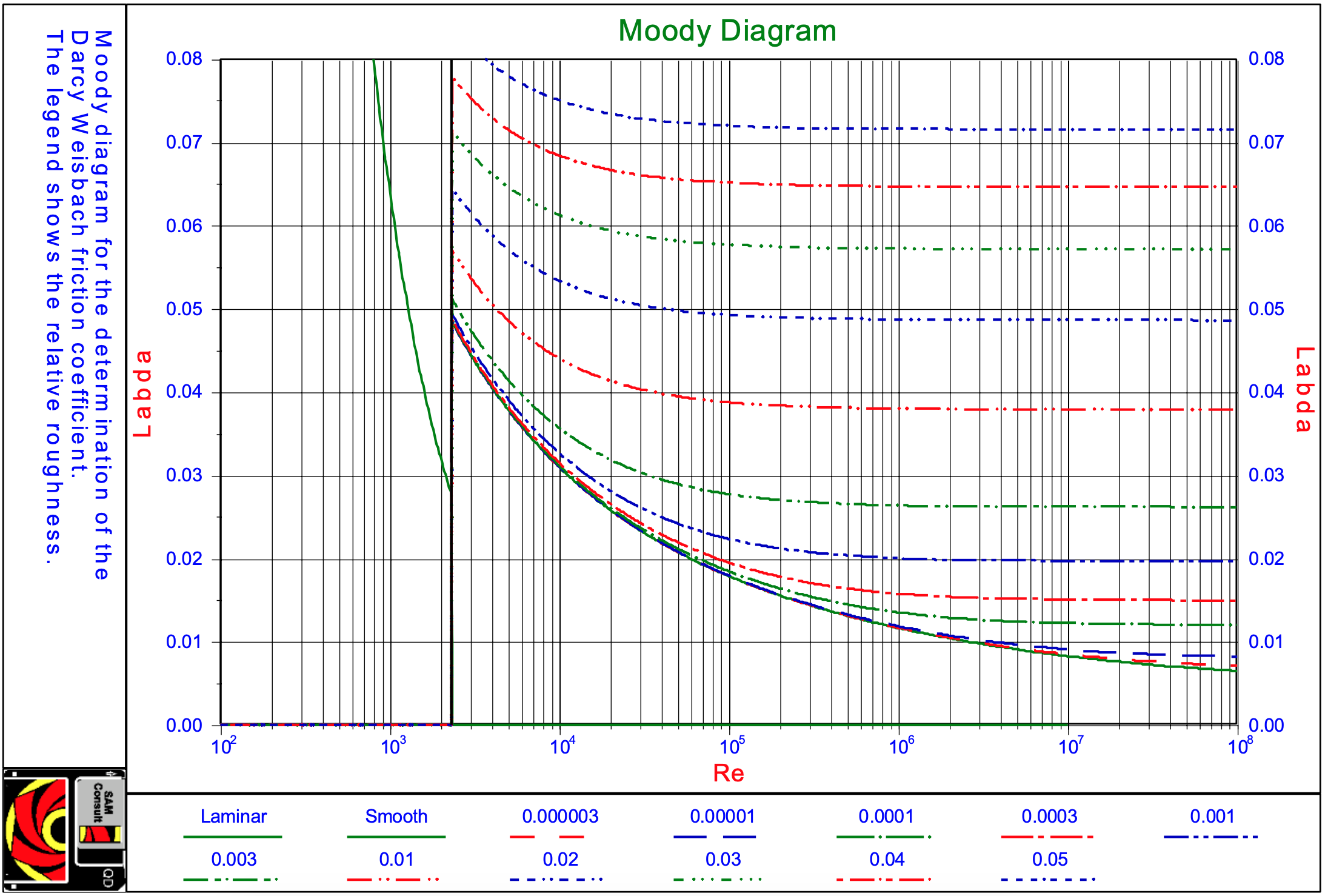
Over the whole range of Reynolds numbers above 2320 the Swamee Jain (1976) equation gives a good approximation:
\[\lambda_{1}=\dfrac{1.325}{\left(\ln \left(\dfrac{\varepsilon}{3.7 \cdot \mathrm{D}_{\mathrm{p}}}+\dfrac{5.75}{\mathrm{Re}^{0.9}}\right)\right)^{2}}=\frac{0.25}{\left(\log _{10}\left(\dfrac{\varepsilon}{3.7 \cdot \mathrm{D}_{\mathrm{p}}}+\dfrac{5.75}{\mathrm{Re}^{0.9}}\right)\right)^{2}} \]


