7.2: Flow Regimes and Scenario’s
- Page ID
- 29228
7.2.1 Introduction
In dredging, the hydraulic transport of solids is one of the most important processes. Since the 50’s many researchers have tried to create a physical mathematical model in order to predict the head losses in slurry transport. We can think of the models of Durand, Condolios, Gibert, Worster, Zandi & Govatos, Jufin Lopatin, Fuhrboter, Newitt, Doron, Wilson, Matousek, Turian & Yuan and the SRC model. Some models are based on phenomenological relations and thus result in semi empirical relations, others tried to create models based on physics, like the two and three layer models. It is however the question whether slurry transport can be modeled this way at all. Observations in our laboratory show a process which is often non-stationary with respect to time and space. Different physics occur depending on the line speed, particle diameter, concentration and pipe diameter. These physics are often named flow regimes; fixed bed with and without sheet flow or suspension, sliding bed, heterogeneous transport, (pseudo) homogeneous transport and sliding flow. It is also possible that more regimes occur at the same time, like, a fixed bed in the bottom layer with heterogeneous transport in the top layer.
It is the observation of the authors that researchers often focus on a detail and sub-optimize their model, which results in a model that can only be applied for the parameters used for their experiments. At high line speeds the volumetric spatial concentration (volume based) and the volumetric transport concentration (volume flux based) are almost equal, because all the particles are in suspension with a small slip related to the carrier liquid velocity. The difference of the head loss between the two concentrations will be within the margin of the scatter of the experiments. At low line speeds however, there may be a sliding or fixed bed, resulting in a big difference between the two concentrations and thus between laboratory and real life situations.
This chapter describes 8 flow regimes and 6 possible scenarios.
The flow regimes for constant spatial volumetric concentration Cvs are, from line speed zero with increasing line speed:
1: Fixed bed without suspension (fine particles) or sheet flow (coarse particles).
2: Fixed bed with suspension (fine particles) or sheet flow (coarse particles).
3: Fixed bed with suspension (fine particles) or sliding bed with sheet flow (coarse particles).
For fine to coarse particles d/Dp<0.015:
5: Heterogeneous transport Cvs≈Cvt.
5/6: Pseudo homogeneous transport, Cvs≈Cvt.
6: Homogeneous transport, Cvs≈Cvt.
For very coarse particles d/Dp>0.015:
7: Sliding flow.
The flow regimes for constant delivered volumetric concentration Cvt are, from line speed zero with increasing line speed:
8: Fixed bed with suspension (fine particles) or sheet flow (coarse particles).
4: Fixed bed with suspension (fine particles) or sliding bed with sheet flow (coarse particles).
For fine to coarse particles d/Dp<0.015:
5: Heterogeneous transport Cvs≈Cvt.
5/6: Pseudo homogeneous transport, Cvs≈Cvt.
6: Homogeneous transport, Cvs≈Cvt.
For very coarse particles d/Dp>0.015:
7: Sliding flow.
3 scenarios are based on a constant volumetric spatial concentration (usually in a laboratory) and 3 scenarios are based on a constant volumetric transport concentration (usually in real life). The flow regimes and scenarios are explained and examples of experiments are given. Based on the experimental evidence, one can conclude that the approach followed in this book gives a good resemblance with the reality.
7.2.2 Concentration Considerations
Based on an analysis of many experiments from literature, 8 flow regimes and 6 scenarios can be distinguished, which will be discussed in the next chapters. In order to understand these 8 flow regimes and 6 scenarios, the difference between the spatial volumetric concentration Cvs and the volumetric transport (delivered) concentration Cvt will first be discussed. In hydraulic transport, 2 definitions of the concentration are often used. Contractors are interested in the delivered volumetric concentration, also named the volumetric transport concentration Cvt. Cvt is defined as the ratio between the volume flow of solids and the volume flow of the mixture. In general one can say that the average solids velocity will be smaller than the average mixture velocity. The difference is called the slip velocity. The spatial volumetric concentration Cvs is defined as the volume of solids divided by the volume of the mixture containing these solids. So the spatial volumetric concentration is based on a volume ratio, while the delivered volumetric concentration is based on a volume flux ratio. Concentration (Cvs) is usually derived from density meter or U-loop readings as:
\[\ \mathrm{C}_{\mathrm{v s}}=\frac{\rho_{\mathrm{m}}-\rho_{\mathrm{l}}}{\rho_{\mathrm{s}}-\rho_{\mathrm{l}}}(\text { density meter }) \quad\text{ or }\quad \mathrm{C}_{\mathrm{v t}}=\frac{\rho_{\mathrm{m}}-\rho_{\mathrm{l}}}{\rho_{\mathrm{s}}-\rho_{\mathrm{l}}}(\mathrm{U}-\mathrm{l o o p})\]
A radioactive density meter reads a density of the entire mass of slurry in the pipe, and thus is best suited to measuring Cvs. In addition the placement of the meter in horizontal or vertical pipe, can affect the readings. A U- tube device reads the delivered density and is thus best suited to measuring Cvt. In a closed loop system, we will know the volume of the closed loop and amount of material added, and thus can calculate Cvs directly, but not necessarily Cvt. The volumetric delivered (transport) concentration is:
\[\ \mathrm{C_{v t}=\frac{\dot{V}_{s}}{\dot{V}_{m}}=\frac{Q_{s}}{Q_{m}}=\frac{v_{s} \cdot A_{s}}{v_{m} \cdot A_{p}}=\frac{v_{s} \cdot C_{v s} \cdot A_{p}}{v_{m} \cdot A_{p}}=C_{v s} \cdot \frac{v_{s}}{v_{m}}}\]
With vs the average velocity of the solids and vm the average velocity of the mixture, also called the line speed vls.
The volumetric spatial concentration is based on the volume ratio solids/mixture according to:
\[\ \mathrm{C}_{\mathrm{v s}}=\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{m}}}\]
The slip velocity vsl is defined as the difference between the velocity of the mixture vm and the velocity of the solids vs:
\[\ \mathrm{v}_{\mathrm{sl}}=\mathrm{v}_{\mathrm{m}}-\mathrm{v}_{\mathrm{s}}=\mathrm{v}_{\mathrm{m}} \cdot\left(\mathrm{1}-\frac{\mathrm{v}_{\mathrm{s}}}{\mathrm{v}_{\mathrm{m}}}\right)=\mathrm{v}_{\mathrm{m}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{vt}}}{\mathrm{C}_{\mathrm{v} \mathrm{s}}}\right)\]
Because of the fact that most experiments are carried out in a closed loop system, the concentration might be determined by the ratio of the volume of solids divided by the volume of the closed loop system.
\[\ \mathrm{C}_{\mathrm{v s}}=\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{c l}}}\]
This means that the concentration of solids in the liquid above the bed will be much smaller once a bed is formed. Now assume a bed with a porosity n of about 40% containing 50% of the solids, matching the v50 of Wilson (1997). This gives for the total bed volume in the closed loop system:
\[\ \mathrm{V}_{\mathrm{b}}=\frac{\mathrm{V}_{\mathrm{s}}}{2} \cdot \frac{\mathrm{1}}{\mathrm{1 - n}}=\frac{\mathrm{C}_{\mathrm{v s}} \cdot \mathrm{V}_{\mathrm{c l}}}{\mathrm{2} \cdot(\mathrm{1}-\mathrm{n})}\]
The volume of solids in suspension is the same, so the volume of the solids in the liquid is:
\[\ \mathrm{V}_{\mathrm{s}, \mathrm{s}=} \frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{2}}\]
The volume of the mixture in suspension above the bed equals the closed loop volume minus the bed volume.
\[\ \mathrm{V}_{\mathrm{m}, \mathrm{s}}=\mathrm{V}_{\mathrm{c l}}-\mathrm{V}_{\mathrm{b}}=\mathrm{V}_{\mathrm{c l}}-\frac{\mathrm{C}_{\mathrm{v s}} \cdot \mathrm{V}_{\mathrm{c l}}}{2 \cdot(1-\mathrm{n})}=\mathrm{V}_{\mathrm{c l}} \cdot\left(\frac{2 \cdot(1-\mathrm{n})-\mathrm{C}_{\mathrm{v} \mathrm{s}}}{\mathrm{2} \cdot(\mathrm{1}-\mathrm{n})}\right)\]
The concentration of the solids in suspension is the volume of these solids, divided by the volume of the closed loop system minus the volume of the bed.
\[\ \mathrm{C}_{\mathrm{vs}, \mathrm{s}}=\frac{\mathrm{V}_{\mathrm{s}}}{2 \cdot \mathrm{V}_{\mathrm{m}, \mathrm{s}}}=\frac{\mathrm{C}_{\mathrm{vs}}}{2 \cdot\left(\frac{2 \cdot(1-\mathrm{n})-\mathrm{C}_{\mathrm{vs}}}{2 \cdot(1-\mathrm{n})}\right)}=\frac{(1-\mathrm{n}) \cdot \mathrm{C}_{\mathrm{vs}}}{2 \cdot(1-\mathrm{n})-\mathrm{C}_{\mathrm{vs}}} \approx \frac{0.6 \cdot \mathrm{C}_{\mathrm{vs}}}{1.2-\mathrm{C}_{\mathrm{vs}}}=\frac{\mathrm{C}_{\mathrm{vs}}}{2-1.66 \cdot \mathrm{C}_{\mathrm{vs}}}\]
Of course the closed loop will not consist of just horizontal parts where a bed may occur, but the above example is just meant to give an indication.
This implies that at low spatial volumetric concentrations Cvs, the concentration in the suspension phase, the heterogeneous transport phase, is 50% of the total volumetric concentration. At a high concentration of Cvs=0.3, the concentration of the heterogeneous phase is still reduced to 0.2. At a concentration of Cvs=0.6, the above equation results in a concentration of 0.6, which makes sense, since this is solid sand and there is no suspension anymore. When experiments are carried out it should be clear which concentration is used. Is it the concentration based on the volume of the closed loop system, giving some constant volumetric spatial concentration? Is it the concentration based on radio active density meters in the pipe section where also the hydraulic gradient is measured, resulting in a spatial volumetric concentration? Or is the concentration measured with a U-tube resulting in a volumetric transport concentration.
Now in a real life production situation there is not a closed loop system, but an open system. There is not a fixed amount of solids in the pipeline, which can be divided in a part in a bed and the rest in suspension. Instead, the supply at the suction mouth can vary from water to twice or more that the delivered concentration. In a stable situation, the production that enters the system is equal to the production that leaves the system. The concentration is determined at the suction mouth and although there may be a bed in part of the pipeline, this does not change the transport concentration, it just increases the line speed and concentration above the bed compared with a pipeline without a bed, due to the conservation of volume in the pipeline. The conclusion of the above considerations is that for a good interpretation of the results of experiments, the method of determining the concentration should be known. It is also important how the results are presented. Graf & Robinson (1970) for example, present their results based on a constant amount of solids in their closed loop system, while Doron & Barnea (1987) connect data points with constant volumetric transport concentration. The presentations of the results are different, while the physics are the same.
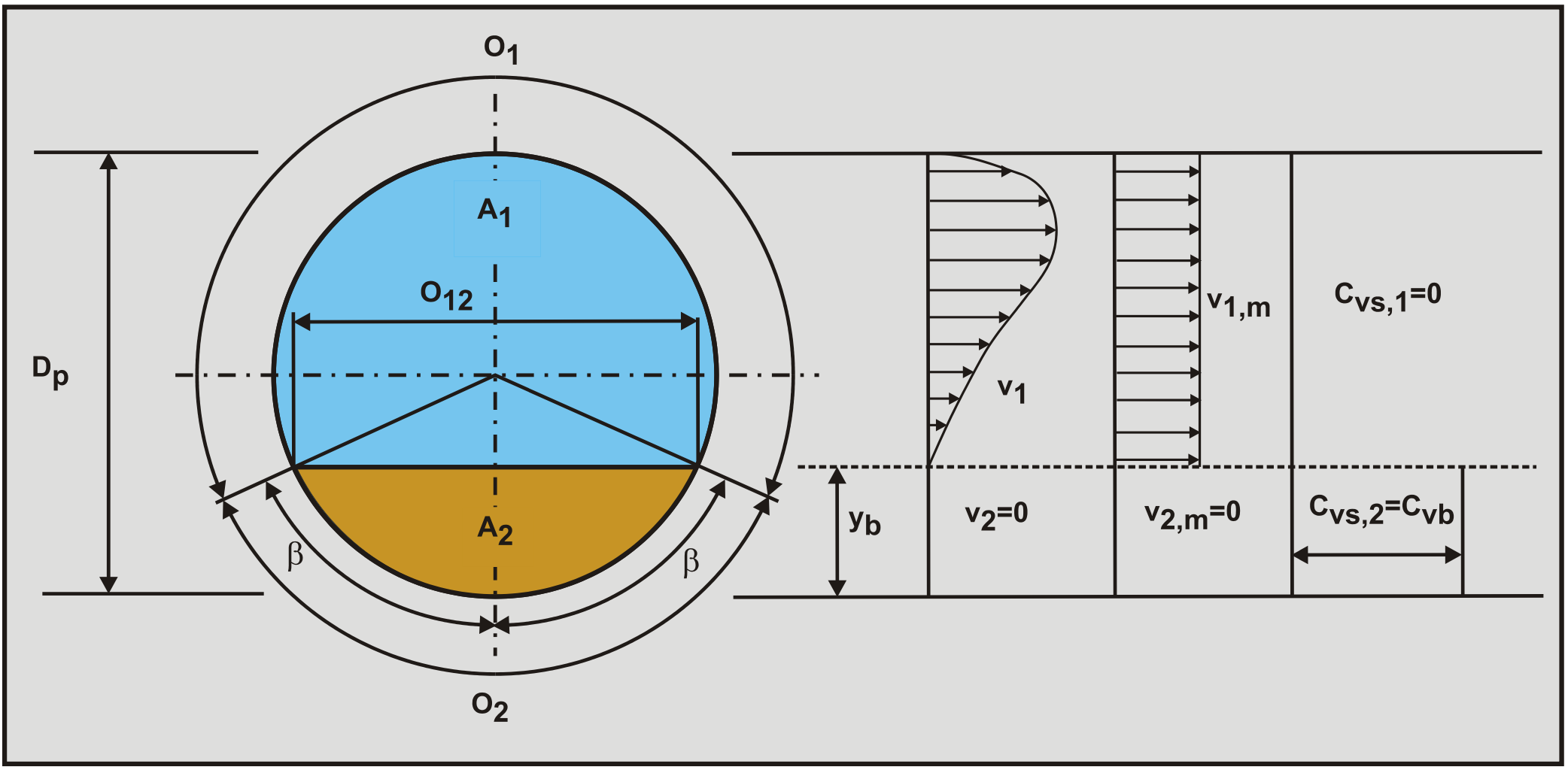
7.2.3 The 8 Flow Regimes Identified
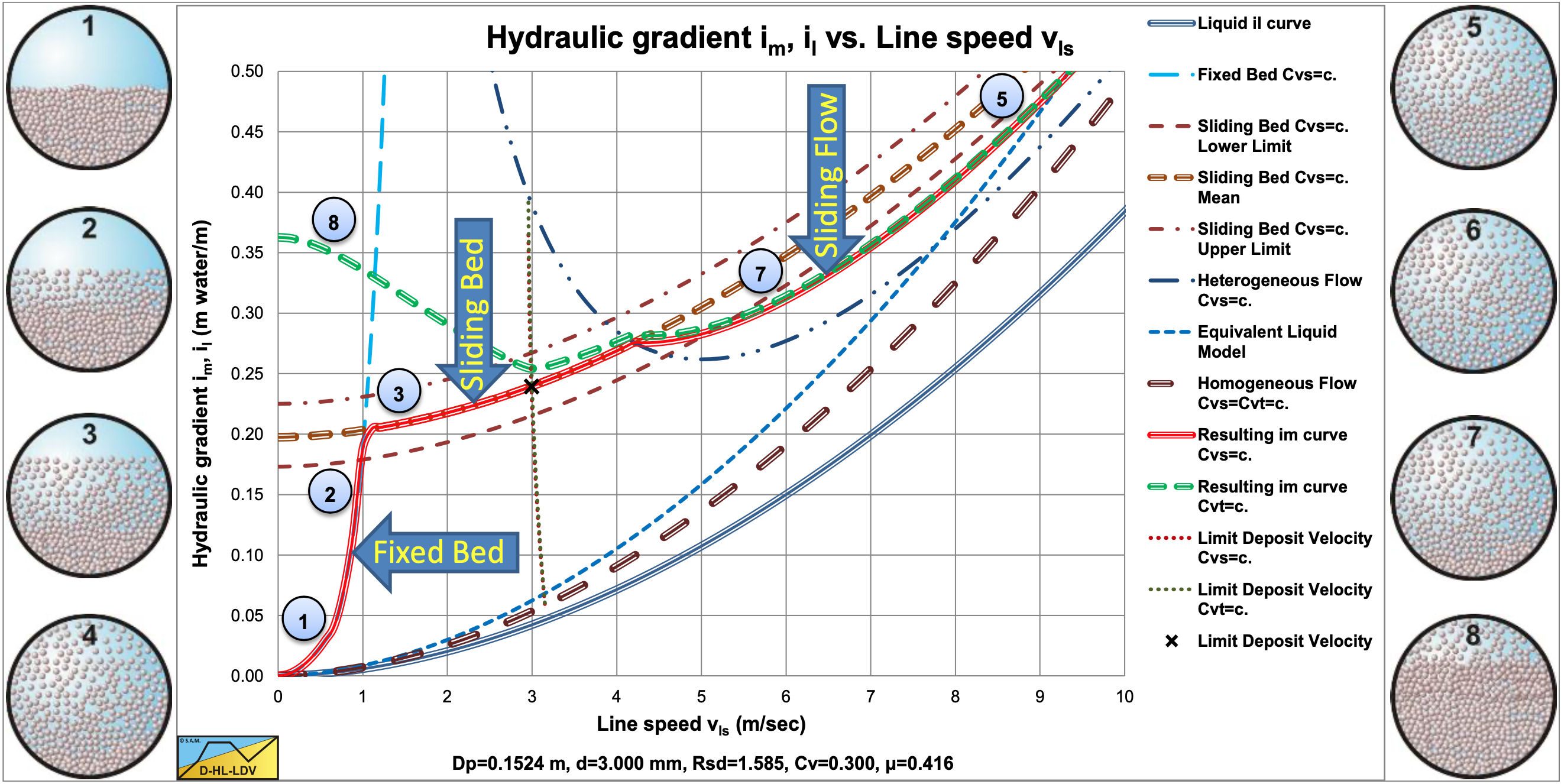
In literature different flow patterns or flow regimes are distinguished. Durand & Condolios (1952) distinguish 4 regimes, based on the particle size. Abulnaga (2002) also distinguished 4 regimes based on the actual flow of particles and their size. Matousek (2004) in his lecture notes distinguishes 6 flow regimes. Here we will consider 8 flow regimes and 6 scenarios for laboratory and real life conditions. These are (Figure 7.2-1 gives some definitions of fully stratified flow in a pipe):
 |
|
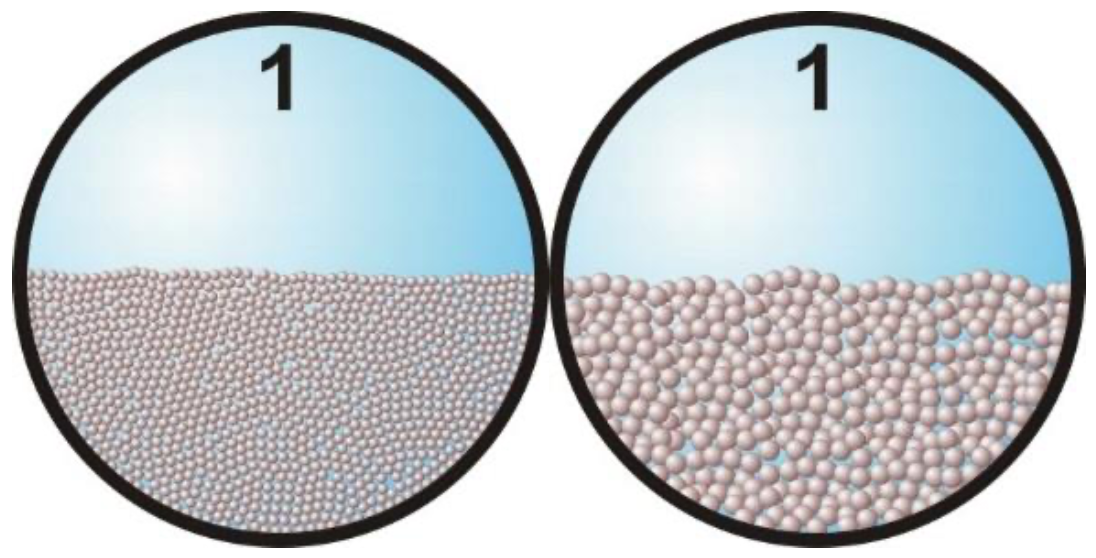
1: Fixed bed without suspension or sheet flow, constant Cvs. Under laboratory circumstances with a constant spatial volumetric concentration Cvs, at low line speeds all the particles are in a stationary (fixed) bed at the bottom of the pipe. Above the bed the liquid is flowing through a smaller cross-section A1=Ap-A2. This gives a higher effective line speed vls,e=vls·Ap/A1. Since the bottom of this cross–section consists of particles, the resulting Darcy-Weisbach friction factor λm has to be determined by taking a weighted average of the friction factor of the liquid-bed interface λ12 and the friction factor of the liquid-pipe wall interface λl. The method of Miedema & Matousek (2014) can be applied to determine the Darcy-Weisbach friction coefficient λ12 on the liquid-bed interface. This method does distinguish between fine and coarse particles. The particle diameter influences the Darcy-Weisbach friction coefficient λ12 by using the particle diameter as the bed roughness. The Shields parameter is below a critical Shields value of about 1 so no sheet flow or suspension occurs. The total pressure loss is thus determined by viscous friction on the liquid-bed interface and the liquid- pipe wall interface, the spatial volumetric concentration and the particle diameter. |
 |
|
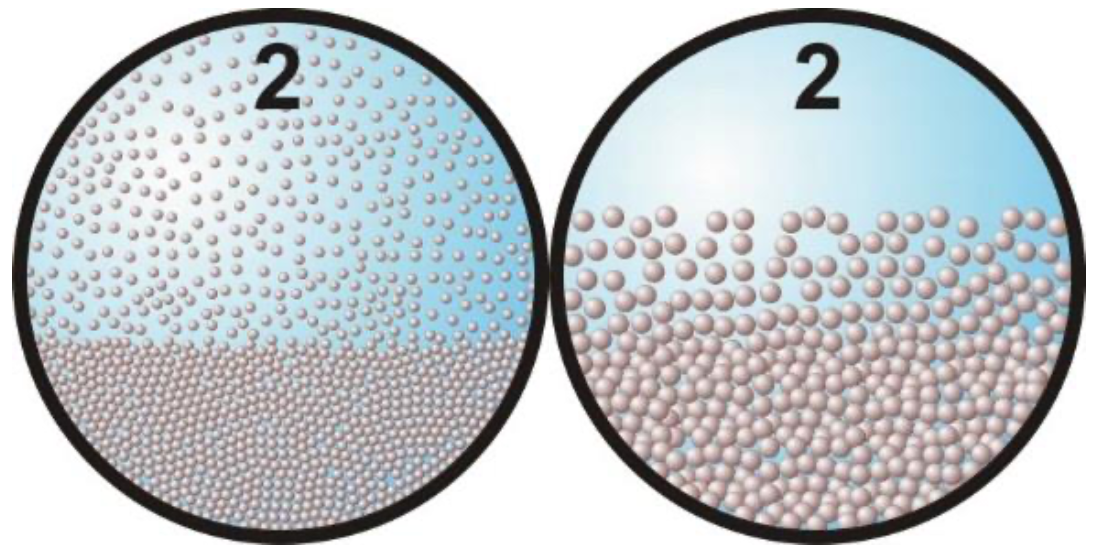
2: Fixed bed with suspension or sheet flow, constant Cvs. Under laboratory circumstances with a constant spatial volumetric concentration Cvs, at medium-low line speeds most of the particles are in a stationary (fixed) bed at the bottom of the pipe. Above the bed a suspension (fine particles) or a sheet flow (coarse particles) is flowing through a smaller cross-section A1=Ap-A2. This gives a higher effective line speed vls,e=vls·Ap/A1. Since the bottom of this cross–section consists of particles, the Darcy- Weisbach friction factor λm has to be determined by taking a weighted average of the friction factor of the liquid-bed interface λ12 and the friction factor of the liquid-pipe wall interface λl. The method of Miedema & Matousek (2014) for sheet flow can be applied to determine the friction coefficient λ12 on the liquid-bed interface. This method does distinguish between fine and coarse particles and gives an explicit relation for the Darcy-Weisbach friction factor. The particle diameter influences the Darcy-Weisbach friction coefficient λ12 slightly. The Shields parameter is above a critical Shields value of about 1, so sediment transport/erosion occurs in the form of sheet flow or suspension. The total pressure loss is thus determined by viscous friction, shear stresses in the sheet flow layer, the spatial volumetric concentration and the particle diameter. |
 |
|
3: Fixed bed with suspension or sliding bed with sheet flow, constant Cvs. Under laboratory circumstances with a constant spatial volumetric concentration Cvs, for coarse particles the bed is sliding with sheet flow at the top, where the thickness of the sheet flow layer increases with an increasing velocity difference between the flow above the bed and the bed, while for fine particles the shear stress on the bed is not high enough to make it start sliding, but more and more particles will be in suspension as the line speed increases. For fine particles the behavior starts following the heterogeneous behavior more and more with increasing line speed. Since coarse particles in sheet flow require an upwards force at least equal to their submerged weight, which results from interparticle forces, an equal downwards force will act on the bed-sheet flow layer interface. The result is a total normal force between the bed and the pipe wall of about the submerged weight of the particles. From experiments it appears that this normal force is almost a constant times the spatial volumetric concentration, according to the Newitt et al. (1955) model. This vertical force times the friction coefficient μsf determines the sliding friction force. The friction coefficient μsf will have a value of about 0.416, but should preferably be determined by experiments, since it is a property of the particles depending on the shape of the particles. The Shields parameter is above a critical Shields value of 1, so sediment transport/erosion occurs. The total pressure loss is thus determined by sliding friction between the bed and the pipe wall for coarse particles and by energy losses due to collisions for fine particles. |
 |
|
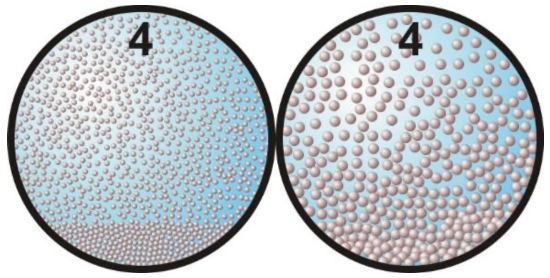
4: Fixed bed with suspension or sliding bed with sheet flow, constant Cvt. Under laboratory circumstances with a constant spatial volumetric concentration Cvs, for coarse particles the bed is sliding with sheet flow, where the thickness of the sheet flow layer increases further with an increasing velocity difference between the flow above the bed and the bed, while for fine particles the shear stress on the bed is not high enough to make it start sliding, but almost all particles will be in suspension as the line speed increases. For fine particles the behavior starts following the heterogeneous behavior as the line speed increases. Since coarse particles in sheet flow require an upwards force at least equal to their submerged weight, which results from interparticle forces, an equal downwards force will act on the bed. The result is a total normal force between the bed and the pipe wall of about the submerged weight of the particles. From experiments it appears that this normal force is almost a constant times the spatial volumetric concentration, according to the Newitt et al. (1955) model. This vertical force times the friction coefficient μsf determines the sliding friction force. The friction coefficient μsf will have a value of about 0.416, but should preferably be determined by experiments, since it is a property of the particles depending on the shape of the particles. The difference with flow regime 3 is, that here the transport/delivered concentration is known. With decreasing line speed and constant delivered volumetric concentration, the spatial volumetric concentration is increasing. The spatial concentration will be higher than the delivered concentration, resulting in a higher resistance. So the constant Cvt curve will always be higher than the constant Cvs curve. The difference increases with decreasing line speed. The Shields parameter is above a critical Shields value of 1, so sediment transport/erosion occurs. The total pressure loss is thus determined by sliding friction between the bed and the pipe wall for coarse particles and by energy losses due to collisions for fine particles. |
 |
|
5: Heterogeneous transport, Cvt≈Cvs. When the line speed increases further, the difference between spatial and delivered concentration becomes smaller. At a certain line speed the macroscopic behavior changes from stationary or sliding bed behavior to heterogeneous behavior. The turbulent forces interacting with the particles are not strong enough to create a uniform distribution throughout the cross-section of the pipe. A definite concentration gradient exists along the vertical profile of the pipe with the highest concentration at the bottom. There may still be deposits, but most particles move in suspension or a sort of sheet flow layer. There is however an interaction between the particles and the bottom of the pipe. These interactions, collisions, cause the loss of kinetic energy of the particles and are the main cause of the pressure losses. Since the number of collisions per unit of time depends mainly on the terminal settling velocity of the particles, it will be almost constant, resulting in pressure losses that are reversely proportional with the line speed or the line speed to a higher power. Since the particles move up and down in the pipe, based on the terminal settling velocity and hindered settling, there are also potential energy losses. The pressure losses can be determined according to Durand & Condolios (1952), Jufin & Lopatin (1966), Miedema & Ramsdell (2013) or others. The heterogeneous model is the same for fine and coarse particles, but the line speed range where it occurs depends on the particle size. The Shields parameter is very high above the Shields curve, resulting in suspension/saltation. The total pressure loss is determined by potential and kinetic energy losses. |
 |
|
6: Homogeneous transport, Cvt≈Cvs. When the line speed increases further, the difference between spatial and delivered concentration becomes smaller and smaller. The turbulent forces interacting with the particles are strong enough to create a uniform distribution throughout the cross-section of the pipe. The turbulent forces interacting with the particles are so strong that the mixture has an almost uniform distribution throughout the cross-section of the pipe. True homogeneous flows is not possible, since for the turbulent forces to overcome gravity, a concentration gradient has to exist. Pseudo homogeneous regimes usually occur with very fine particles or at very high line speeds. The pressure losses in this regime can be modeled using the adapted/modified equivalent liquid model (ELM). It is assumed that the spatial volumetric concentration Cvs and the volumetric transport (delivered) concentration Cts are almost equal. The Shields parameter is very high above the Shields curve, resulting in a suspension. The total pressure loss is determined by the work carried out by lift forces and turbulent dispersion. |
|
5/6: Pseudo homogeneous transport, Cvt≈Cvs. At the line speed where heterogeneous and homogeneous transport meet, there will be a transition between the two regimes. If the turbulent near wall lift force equals the submerged weight of the particle, this lift force will prevent the particles from hitting the bottom of the pipe, resulting in a sudden drop of the heterogeneous pressure losses. At slightly higher line speeds the lift force is strong enough to push the particles into the turbulent flow, where turbulent dispersion will take care of further mixing. In between there may be a gap resulting in almost no additional pressure losses. This occurs for particles with diameter from 0.1-0.5 mm with bigger pipe diameters. The pressure losses can be determined according to Miedema &Ramsdell (2013). The Shields parameter is very high above the Shields curve, resulting in a suspension. The total pressure loss is determined by decreasing potential and kinetic energy losses and by increasing equivalent liquid model (ELM) behavior. |
 |
|
7: Sliding Flow. At relatively low concentrations and relatively small particle diameters, the sliding bed regime will have a transition to the heterogeneous regime at the intersection of the two regimes. This is the result of lift forces strong enough to lift the particles and turbulent dispersion to mix them into a heterogeneous mixture. However when the weight of the bed is bigger than the total lift forces, this will not occur and the particles stay in the bed in a sort of sheet flow. A second reason may be that at high concentrations the space above the bed is not big enough to fully develop turbulence. The pressure losses in this regime are much higher than the pressure losses with heterogeneous transport at lower concentrations. The pressure losses can be determined according to Miedema &Ramsdell (2013). The term Sliding Flow is chosen, because there is flow but the flow resistance has the character of sliding friction. The Shields parameter is far above the Shields curve, so sediment transport/erosion occurs. The total pressure loss is thus determined by a combination of sliding friction between the bed and the pipe wall and kinetic and potential energy losses. The larger the particle diameter to pipe diameter ratio, the more this tends to sliding friction behavior and the smaller the heterogeneous contribution. |
 |
|
8: Fixed bed with suspension, constant Cvt. Under real life conditions, there will be a “constant” volumetric transport concentration with decreasing line speed. There will be equilibrium between erosion and deposition, resulting in a certain bed height. Gibert (1960) has proposed that the Froude number will be equal to the Froude number at the Limit Deposit Velocity. In this case, the Limit Deposit Velocity is defined as the velocity where the sliding bed has vaporized due to erosion. With decreasing line speed, the bed height increases and so do the pressure losses. Once the bed height is known, the pressure losses can be determined according to the Newitt et al. (1955) model. This regime occurs if the relative excess hydraulic gradient is high enough to result in a sliding bed and so this will occur much more with small pipe diameters then with large pipe diameter. The Shields parameter is above the a critical Shields value, so erosion occurs. The total pressure loss is thus determined by sliding friction between the bed and the pipe wall, where the spatial concentration is increasing with decreasing line speed, while the transport concentration is a constant. |
7.2.4 The 6 Scenario’s Identified
In pipes with small diameters the hydraulic gradient will be relatively high, resulting in relatively high hydraulic gradients when transporting a mixture. This results in hydraulic gradients approaching the hydraulic gradient required to create a sliding bed. In pipes with large diameters the hydraulic gradient will be relatively small, also resulting in relatively small hydraulic gradients when transporting a mixture. This results in hydraulic gradients too small compared with the hydraulic gradient required to create a sliding bed.
From the 8 flow regimes, 6 scenarios can be constructed, where a scenario does not have to contain all 8 flow regimes. A scenario describes the flow regime behavior when the line speed increases from zero to a certain maximum. This maximum is arbitrary but should be related to practical line speeds. So this maximum increases with increasing pipe diameter.
The 8 flow regimes and 6 scenarios are shown in Figure 7.2-2, Figure 7.2-3, Figure 7.2-4, Figure 7.2-5, Figure 7.2-6 and Figure 7.2-7. Figure 7.2-2 and Figure 7.2-3 show the scenario’s L1 for laboratory conditions and R1 for real life conditions for fine sands. Figure 7.2-4 and Figure 7.2-5 show the scenario’s L2 for laboratory conditions and R2 for real life conditions for coarse sands. Figure 7.2-6 and Figure 7.2-7 show the scenario’s L3 for laboratory conditions and R3 for real life conditions for gravels.
The difference between laboratory conditions and real life conditions can be found at low line speeds where the volumetric spatial Cvs and transport Cvt concentrations differ substantially due to slip. At higher line speeds with heterogeneous and (pseudo) homogeneous transport it is assumed that the slip velocity vsl is small compared to the line speed vls.
Most of the graphs are made for sands and gravels with water as the carrier liquid, however the modelling is also valid for other solids and other liquids.
7.2.4.1 Scenarios L1 & R1
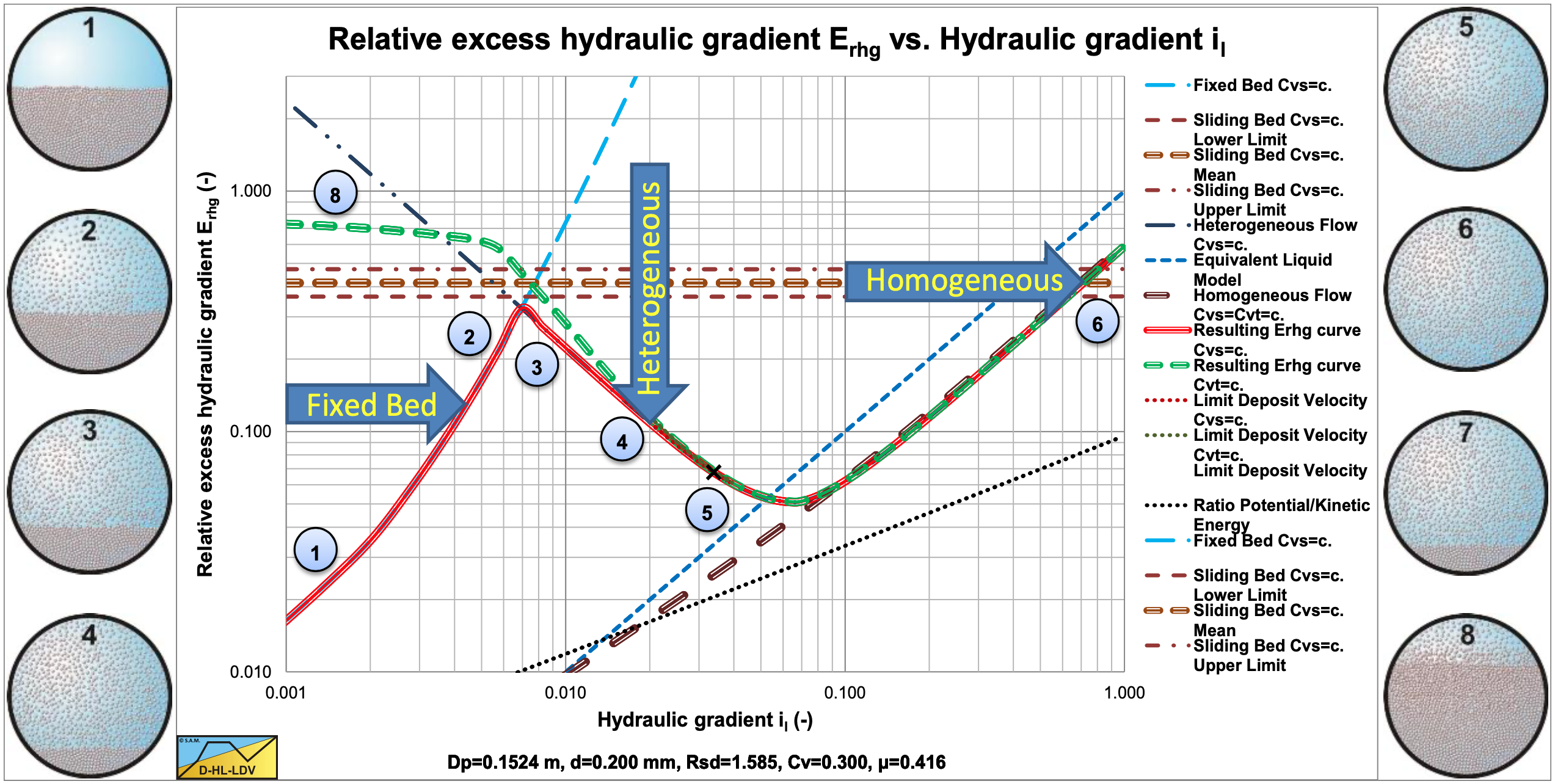
|
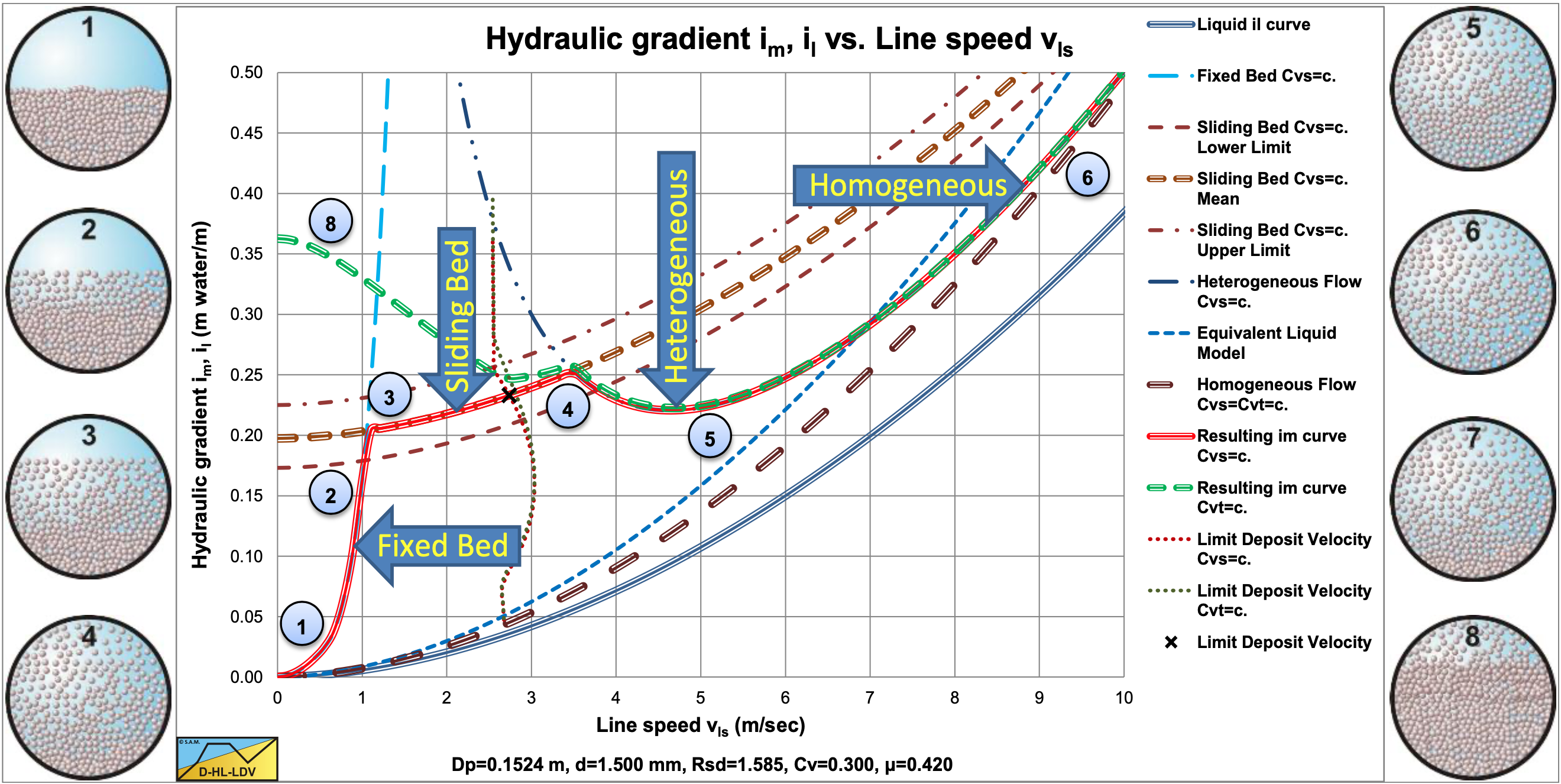
Scenario L1 (the red solid line) Table 7.2-3: Indication of occurrence of L1.  Starting at a line speed vls=0, there will be a stationary (fixed) bed (1). When the line speed is increased, there will not be erosion until the Shields parameter is high enough above the Shields curve. Increasing the line speed further will result in erosion and suspension or sheet flow of the particles (2). The upwards directed solid red curve becomes steeper. At a certain line speed, the macroscopic behavior will have a transition from fixed bed to heterogeneous (3). This also means that the excess pressure losses go from shear stress dominated to collision dominated. Increasing the line speed further results in heterogeneous transport (5). The solid red curve is downwards directed. The Limit Deposit Velocity is somewhere in the heterogeneous flow regime. Increasing the line speed further, results in a transition region between heterogeneous transport and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The solid red curve is upwards directed again. Scenario R1 (the green dashed line) Table 7.2-4: Indication of occurrence of R1.  Starting at a line speed vls=0, there will be equilibrium between erosion and deposition, resulting in a certain bed height. Above the bed there will be heterogeneous transport or suspension. At very low line speeds, the hydraulic gradient is so high that a sliding bed may occur (8). At these low line speeds, it is also possible that only part of the bed is siding resulting in sliding friction that is not fully mobilized. The green dashed curve is slightly downwards directed. The height of the green dashed line depends on the Cvt. A smaller Cvt gives a higher green dashed line, because a smaller Cvt will have more slip. The red solid line (constant Cvs) is hardly influenced by the spatial concentration. At higher line speeds, the bed has a higher velocity and starts vaporizing, the hydraulic gradient drops, resulting in a transition towards heterogeneous behavior (4) and at higher line speeds full heterogeneous behavior (5). The dashed green line is downwards directed. The Limit Deposit Velocity is somewhere in the heterogeneous flow regime. Increasing the line speed further, results in a transition region between heterogeneous transport and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The green dashed line is upwards directed again. The solid red line and the dashed green line coincide. |
7.2.4.2 Scenarios L2 & R2
|
Scenario L2 (the red solid line) Table 7.2-6: Indication of occurrence of L2. 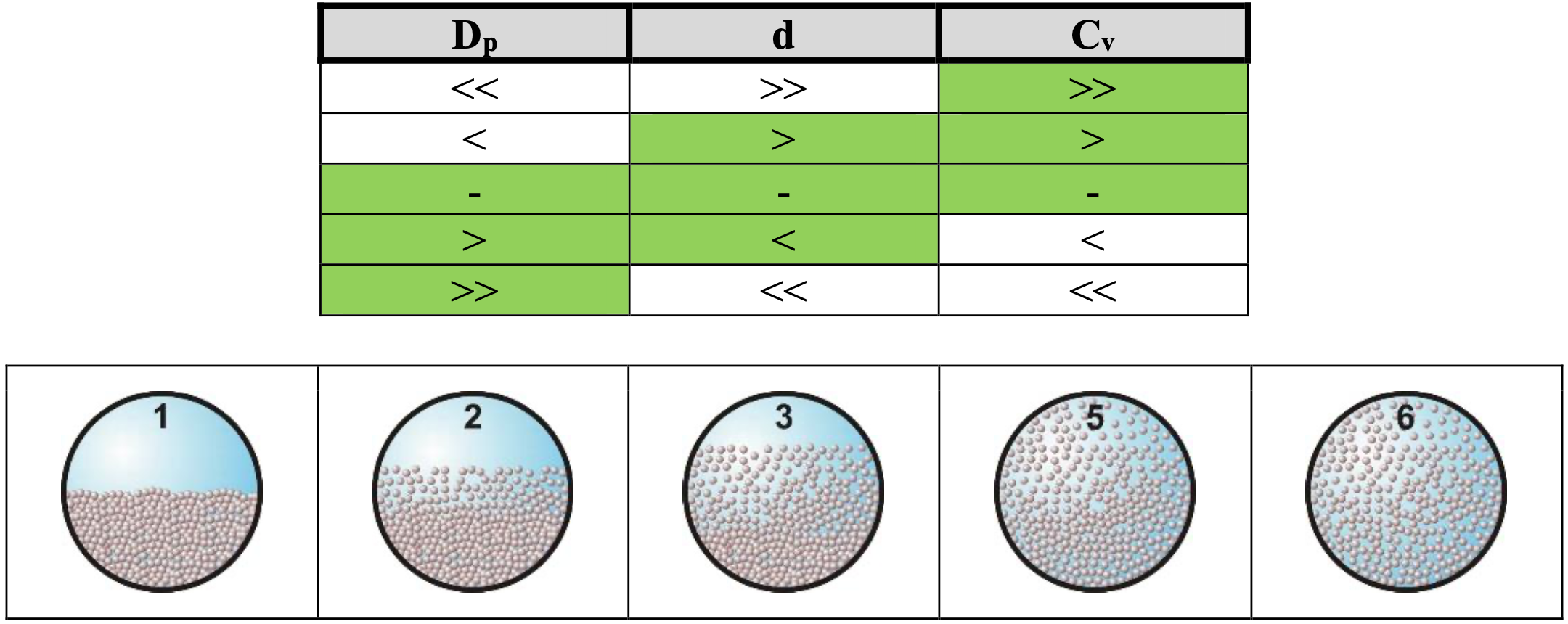 Starting at a line speed vls=0, there will be a stationary (fixed) bed (1). When the line speed is increased, there will not be erosion until the Shields parameter is high enough above the Shields curve. Increasing the line speed further will result in erosion and suspension or sheet flow of the particles (2). The upwards directed solid red curve becomes steeper. At a certain line speed, the hydraulic gradient is high enough to make the bed to start sliding (3). Increasing the line speed further will result in an increase of the velocity of the bed and an increase of the erosion. The relative excess hydraulic gradient remains constant, because the weight of the suspension and the bed is a constant, resulting in an almost constant friction force. Increasing the line speed further will give a transition to heterogeneous transport (5). The solid red line is first horizontal and then downwards directed. The Limit Deposit Velocity is somewhere at the right of the sliding bed regime. Increasing the line speed further, results in a transition region between heterogeneous transport and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The solid red curve is upwards directed again. Scenario R2 (the green dashed line) Table 7.2-7: Indication of occurrence of R2. 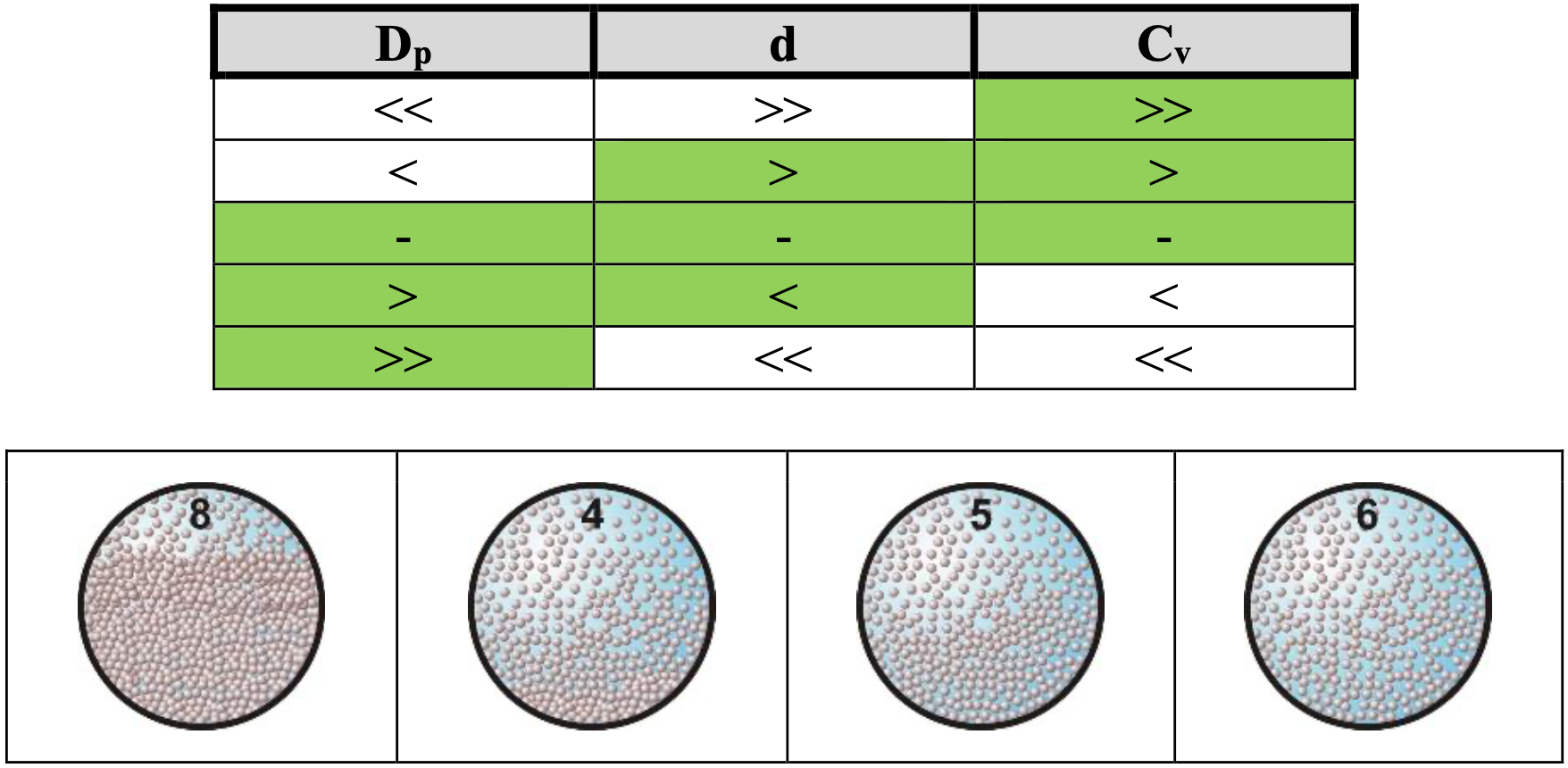 Starting at a line speed vls=0, there will be equilibrium between erosion and deposition, resulting in a certain bed height. Above the bed there will be heterogeneous transport or suspension. At very low line speeds, the hydraulic gradient is so high that a sliding bed may occur (8). At these low line speeds, it is also possible that only part of the bed is siding resulting in sliding friction that is not fully mobilized. The green dashed curve is slightly downwards directed. The height of the green dashed line depends on the Cvt. A smaller Cvt gives a higher green dashed line, because a smaller Cvt will have more slip. The red solid line (constant Cvs) is hardly influenced by the spatial concentration. At higher line speeds, the bed has a higher velocity and starts vaporizing, the hydraulic gradient drops, resulting in a transition towards heterogeneous behavior (4) and at higher line speeds full heterogeneous behavior (5). The dashed green line is downwards directed. The Limit Deposit Velocity is somewhere at the right of the sliding bed regime. Increasing the line speed further, results in a transition region between heterogeneous transport and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The solid red curve is upwards directed again. |
7.2.4.3 Scenarios L3 & R3
|
Scenario L3 (the red solid line) Table 7.2-9: Indication of occurrence of L3.  Starting at a line speed vls=0, there will be a stationary (fixed) bed (1). When the line speed is increased, there will not be erosion until the Shields parameter is high enough above the Shields curve. Increasing the line speed further will result in erosion and suspension or sheet flow of the particles (2). The upwards directed solid red curve becomes steeper. At a certain line speed, the hydraulic gradient is high enough to make the bed to start sliding (3). Increasing the line speed further will result in an increase of the velocity of the bed and an increase of the erosion. The relative excess hydraulic gradient remains constant, because the weight of the suspension and the bed is a constant, resulting in an almost constant friction force. Increasing the line speed further will give a transition to sliding flow (7). The solid red line is first horizontal and then slightly downwards directed. The Limit Deposit Velocity is somewhere at the right of the sliding bed regime or in the sliding flow regime. Increasing the line speed further, results in a transition region between sliding flow and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The solid red curve is upwards directed again. Scenario R3 (the green dashed line) Table 7.2-10: Indication of occurrence of R3. 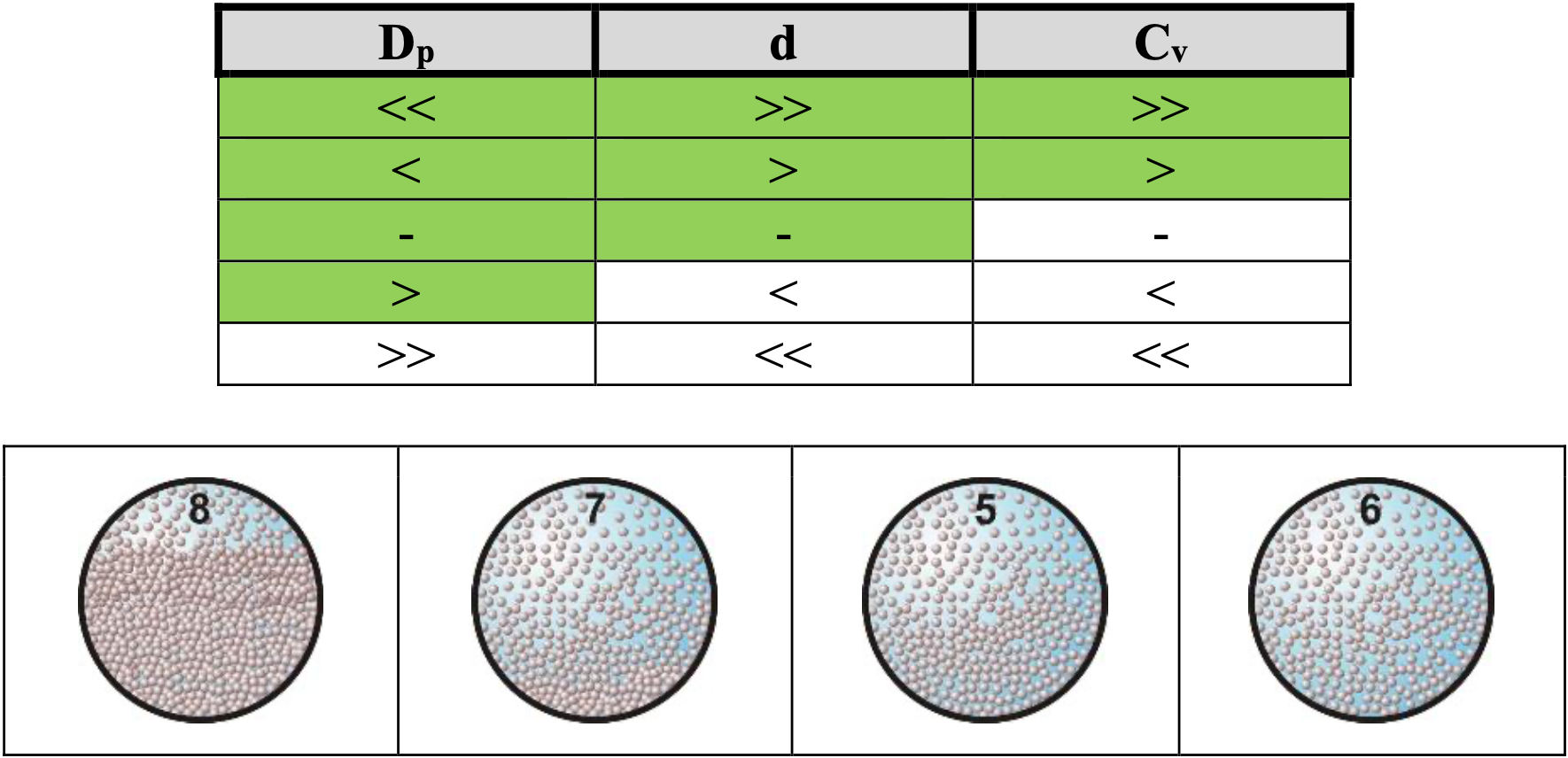 Starting at a line speed vls=0, there will be equilibrium between erosion and deposition, resulting in a certain bed height. Above the bed there will be heterogeneous transport or suspension. At very low line speeds, the hydraulic gradient is so high that a sliding bed may occur (8). At these low line speeds, it is also possible that only part of the bed is siding resulting in sliding friction that is not fully mobilized. The green dashed curve is slightly downwards directed. The height of the green dashed line depends on the Cvt. A smaller Cvt gives a higher green dashed line, because a smaller Cvt will have more slip. The red solid line (constant Cvs) is hardly influenced by the spatial concentration. At higher line speeds, the bed has a higher velocity and starts vaporizing, the hydraulic gradient drops, resulting in a transition towards sliding flow behavior (7) and at higher line speeds full heterogeneous behavior (5). The dashed green line is slightly downwards directed. The Limit Deposit Velocity is somewhere at the right of the sliding bed regime or in the sliding flow regime. Increasing the line speed further, results in a transition region between heterogeneous transport and (pseudo) homogeneous transport (5/6). At very high line speeds, the regime will be the homogeneous regime (6). Whether this regime will be reached with practical line speeds depends completely on the combination of the parameters involved. The solid red curve is upwards directed again. |
7.2.4.4 Conclusions & Discussion
From Figure 7.2-2, Figure 7.2-3, Figure 7.2-4, Figure 7.2-5, Figure 7.2-6 and Figure 7.2-7. it is clear that the characterization of flow regimes of Durand (1952), Abulnaga (2002) or Matousek (2004) is not adequate enough to identify all possible scenarios. Flow regime graphs like the ones published by Newitt (1955) or King (2002) (based on Turian & Yuan (1977)) already give a better understanding. These graphs however do not show the difference between laboratory (Cvs) and real life (Cvt) conditions and do not take the sliding flow effect into account, probably because the volumetric concentrations were not high enough.
7.2.5 Verification & Validation
The Relative Excess Hydraulic Gradient Erhg is the contribution of the solids to the relative hydraulic gradient. The word relative is used here because the hydraulic gradient is divided by the volumetric concentration Cv and the relative submerged density Rsd in order to determine the Erhg. The Erhg can be applied for all flow regimes. The relative submerged density Rsd is defined as:
\[\ \mathrm{R}_{\mathrm{s d}}=\frac{\rho_{\mathrm{s}}-\rho_{\mathrm{l}}}{\rho_{\mathrm{l}}}\]
The Slip Relative Squared Srs is the Slip Velocity of a particle vsl divided by the Terminal Settling Velocity of a particle vt squared and this Srs value is a good indication of the excess pressure losses due to the kinetic energy losses of the solids. The Settling Velocity Hindered Relative Shr is the ratio between the hindered settling velocity vt·(1-Cv/κ)β and the line speed vls, divided by the relative submerged density Rsd and the volumetric concentration Cv. The Shr value gives a good approximation of the potential energy losses of the solids. The Shr and Srs are derived and can be applied for the heterogeneous regime.
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{v}}}=\mathrm{R}_{\mathrm{ss}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\left(\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{l s}}}\right)+\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}\]
The Stratification Ratio of the Solids R is a measure for the level of stratification of slurry as introduced by Wilson et al. (1997). A high stratification ratio means that the slurry is (almost) fully stratified; the liquid phase and the sediment (bed) phase are almost separated.
Under laboratory conditions with constant volumetric spatial concentration Cvs, the Erhg is limited by the value of the sliding friction coefficient μsf. The lower limit of the Erhg is when the heterogeneous regime transits to the (pseudo) homogeneous regime. Also here the Srs is derived and can be applied for the heterogeneous regime only. Resuming, the Erhg is valid for all flow regimes, the Srs is valid for the heterogeneous regime and the friction factor μsf is valid for the sliding bed regime. In the following examples the Erhg(il) graph will be used. The advantage of the Erhg(il) graph is that this type of graph is almost independent of the values of concentration Cvs and relative submerged density Rsd, but also almost independent of the pipe wall roughness and the temperature (kinematic viscosity). A disadvantage may be that it will take more effort to transform this graph back to real life data, the hydraulic gradient or pressure versus the line speed.
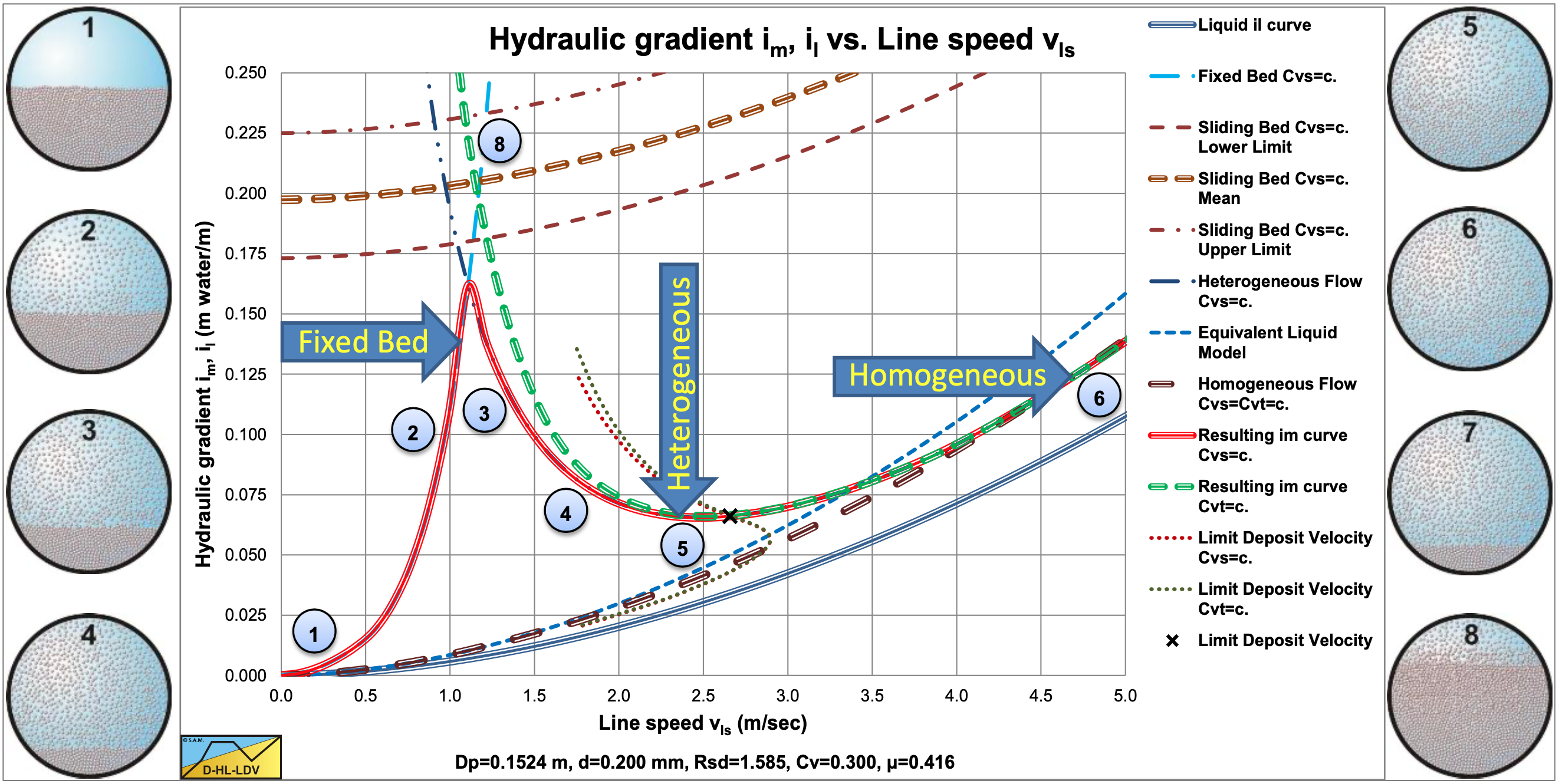
In these graphs always the lines for fixed/stationary bed (constant Cvs, thick solid red upwards on the left), ELM (thin dashed dark blue, upwards), homogeneous transport (thick dashed dark brown, upwards), heterogeneous transport (Cvs thick solid red downwards, Cvt thick dashed green downwards), sliding bed (Cvs thick solid red horizontal and constant Cvt thick dashed green slightly downwards) are drawn, in order to form a reference system.
The graphs show 3 additional lines. The thin dotted black line shows the ratio of the potential energy to the kinetic energy for heterogeneous transport. The thin blue dash-dot-dot line shows the heterogeneous curve without transitions to other flow regimes. The thin brown dash-dot-dot line shows the mobilization of homogeneous transport. The latter two lines added give the transition from the heterogeneous to the homogeneous flow regime.
All data are compared with the DHLLDV Framework.
7.2.5.1 L1: Fixed Bed & Heterogeneous, Constant Cvs
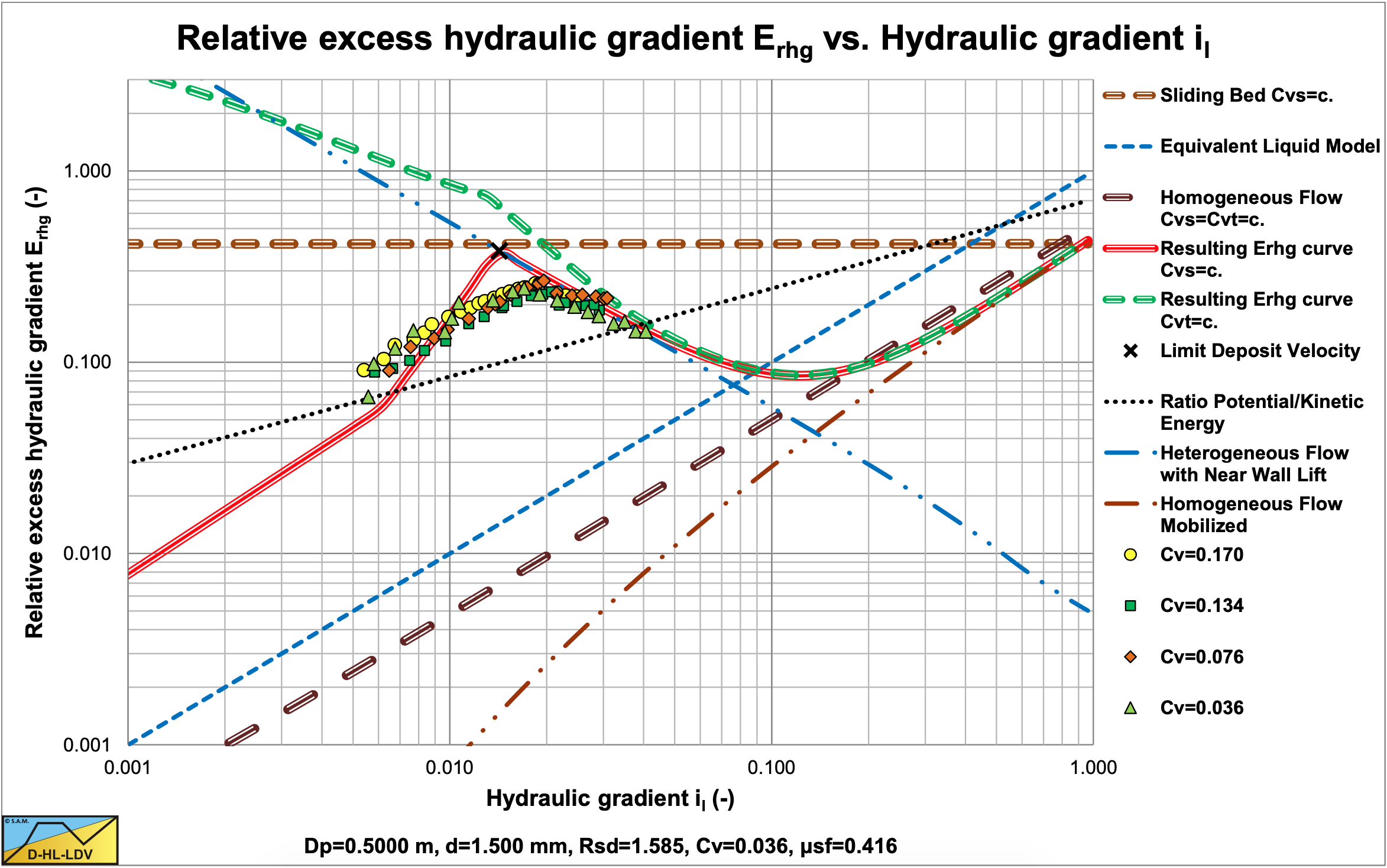
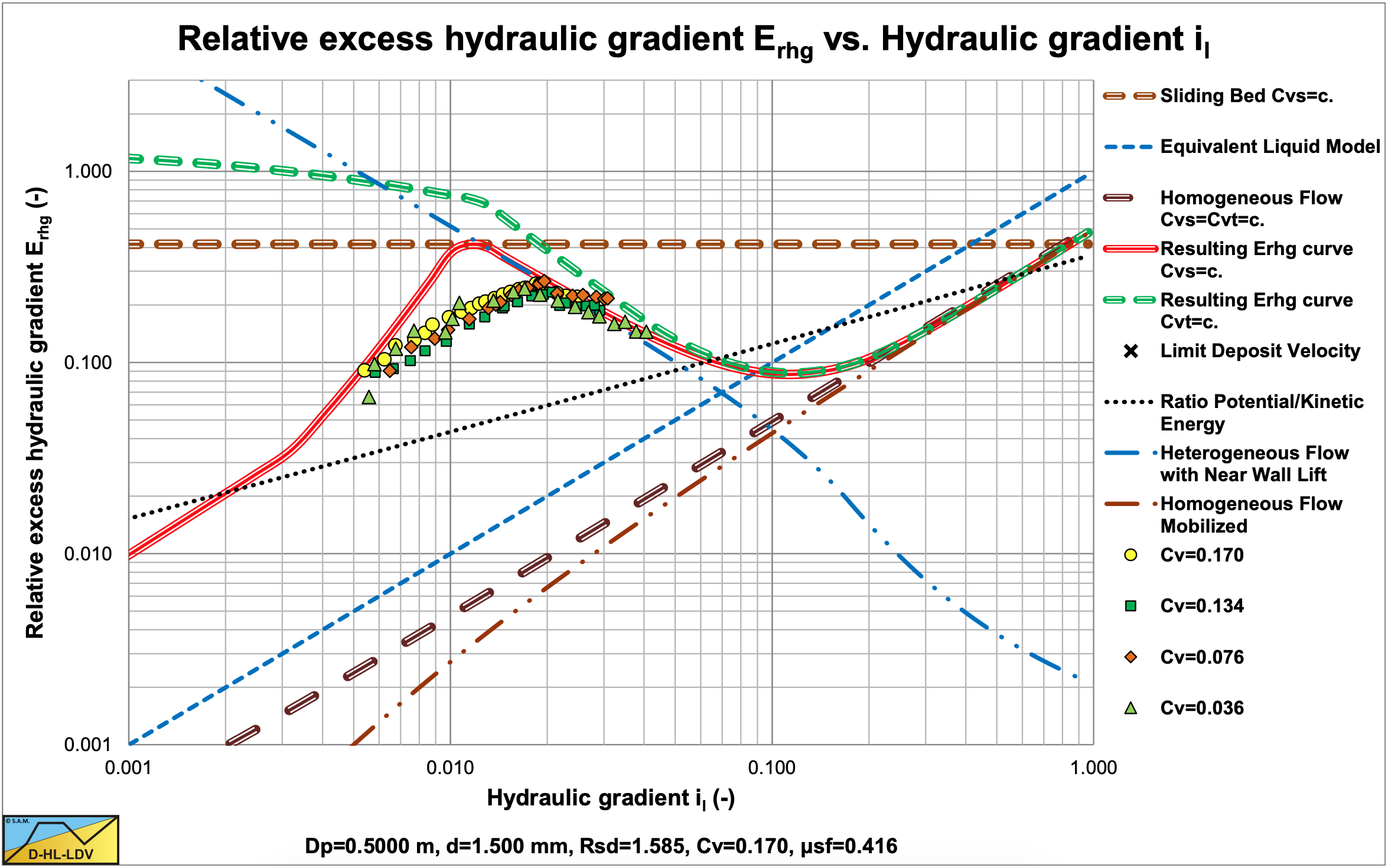
These experiments clearly show the transition of a fixed bed (flow regimes 1 and 2) to heterogeneous transport (flow regime 5) at a constant volumetric spatial concentration. The solid lines are drawn for a Cvs=0.036 & 0.17 and may differ slightly for other concentrations. The transition is smoother than the DHLLDV Framework predicts.
7.2.5.2 R1: Heterogeneous, Constant Cvt
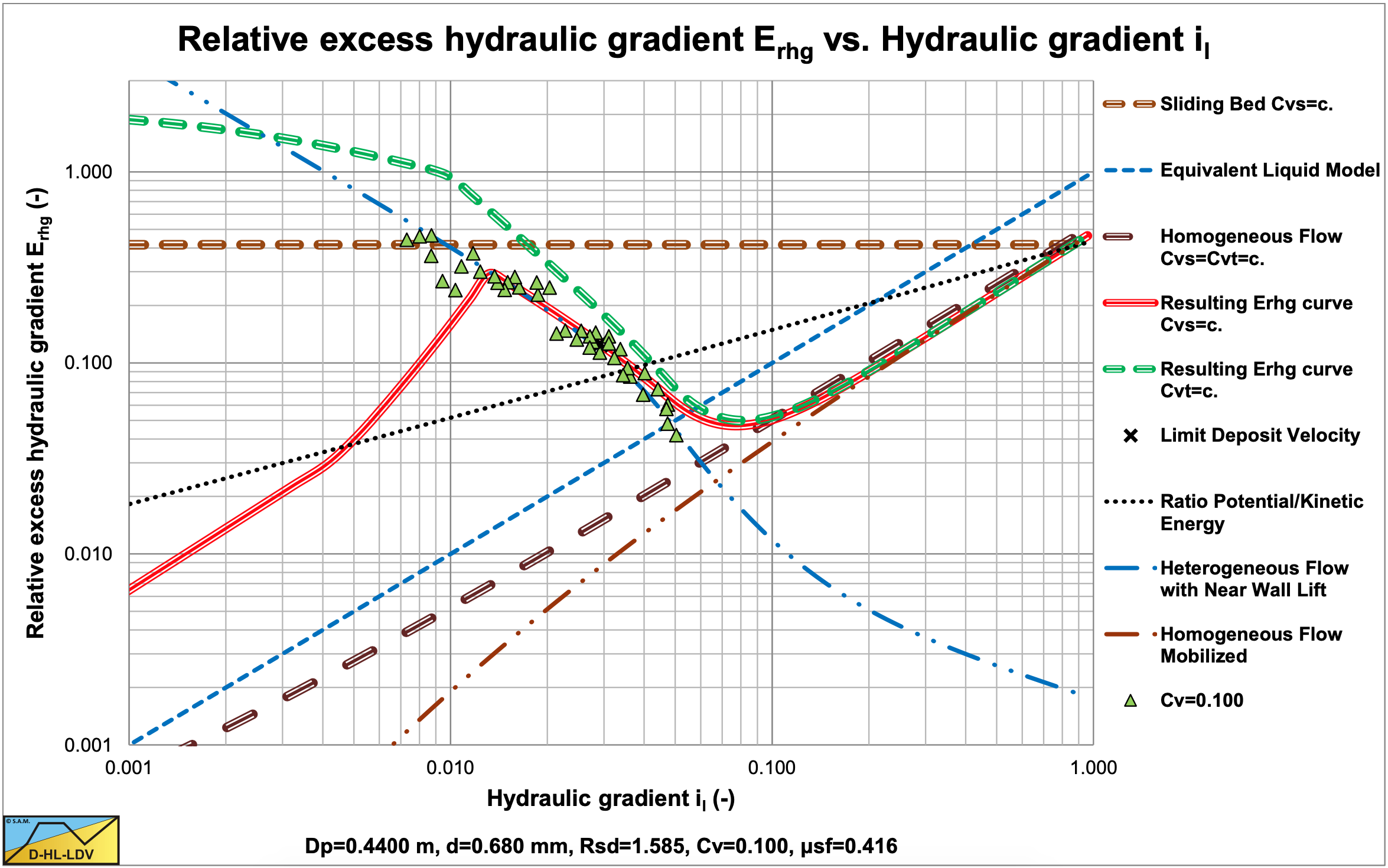
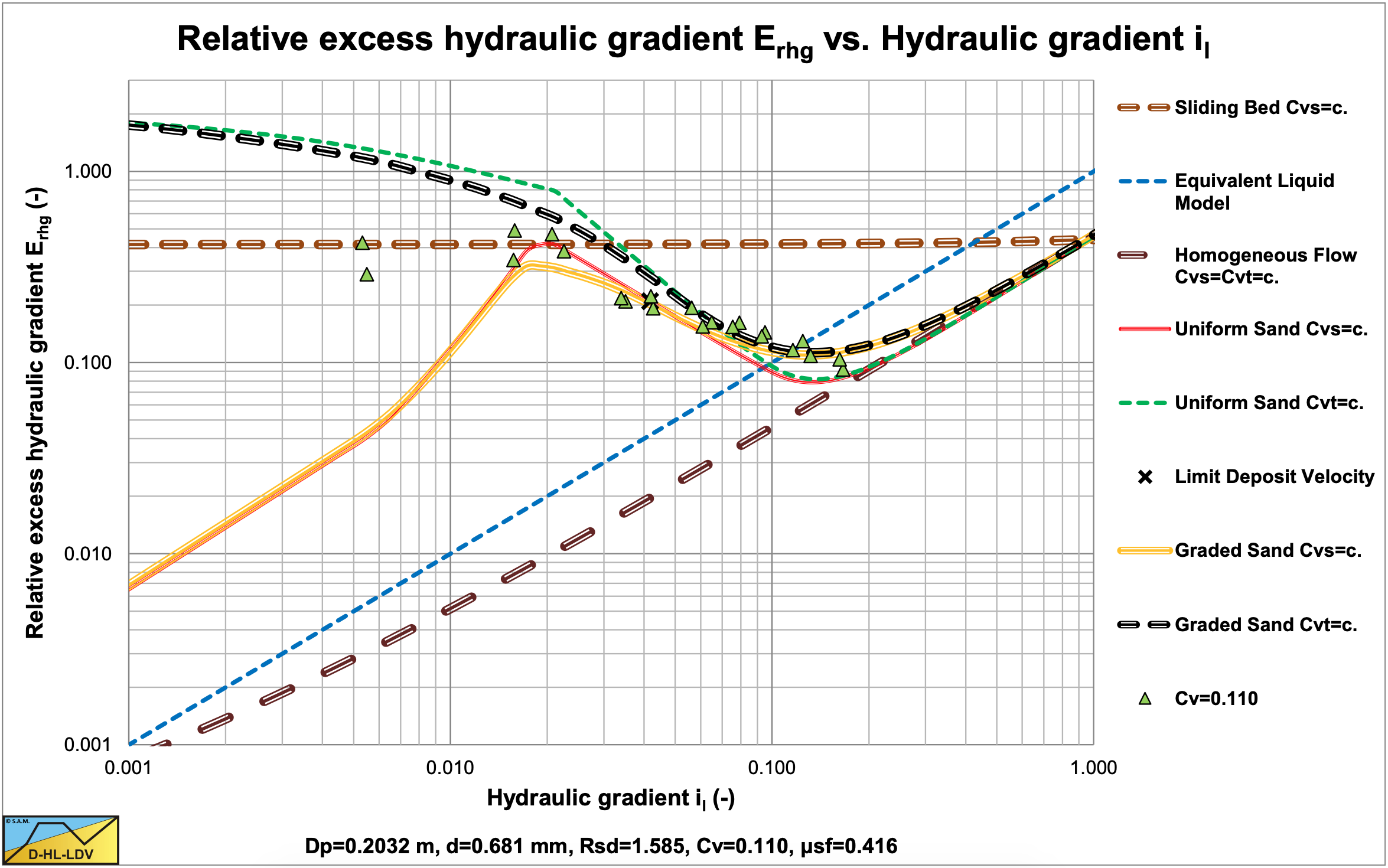
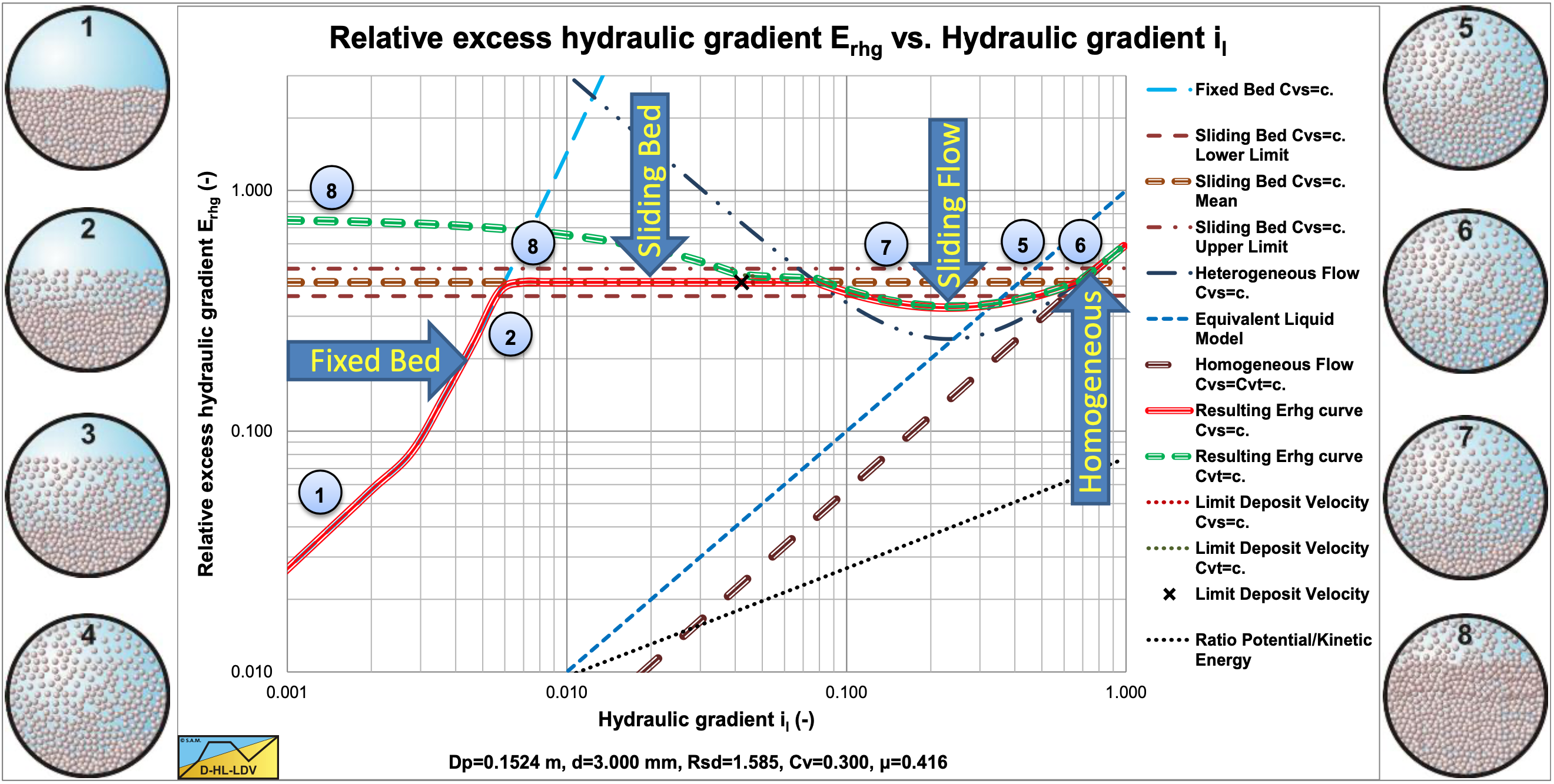
These experiments show that at line speeds below the Limit Deposit Velocity and constant Cvt, the heterogeneous line is still followed. The grading of the sand makes the heterogeneous curve less steep, but this depends on the grading, the particle size and the pipe diameter.
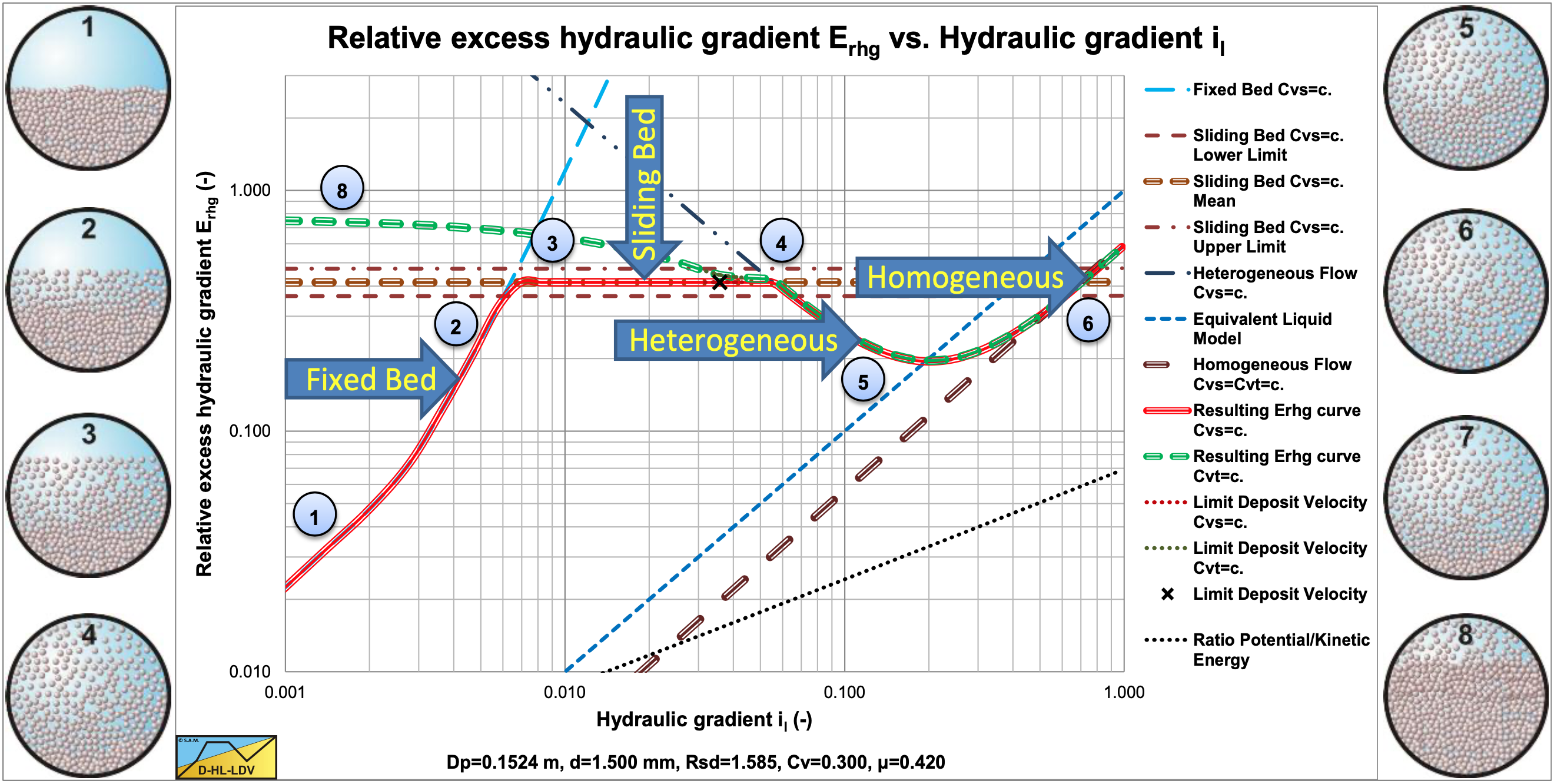
7.2.5.3 L2: Fixed & Sliding Bed – Heterogeneous & Sliding Flow, Constant Cvs
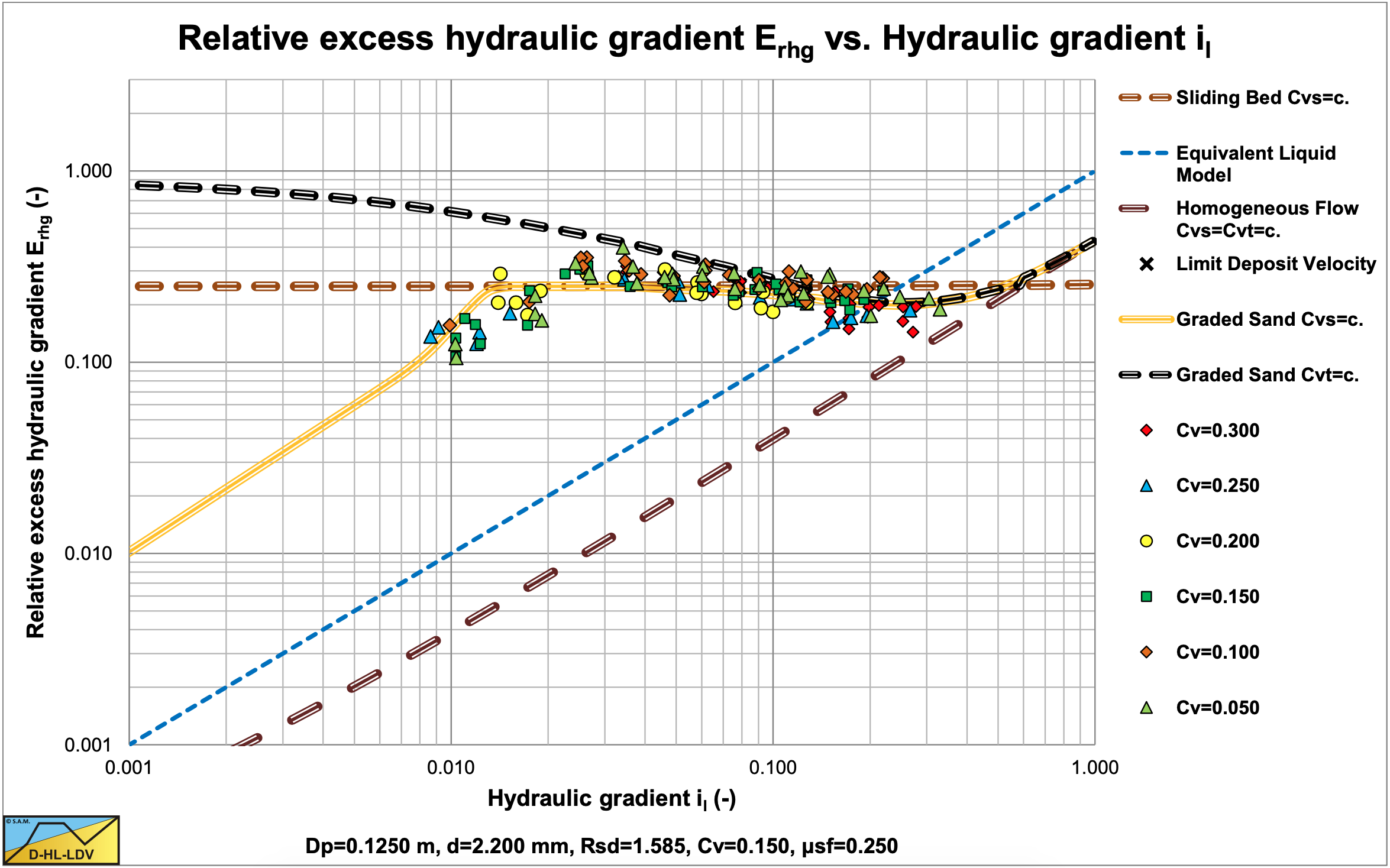
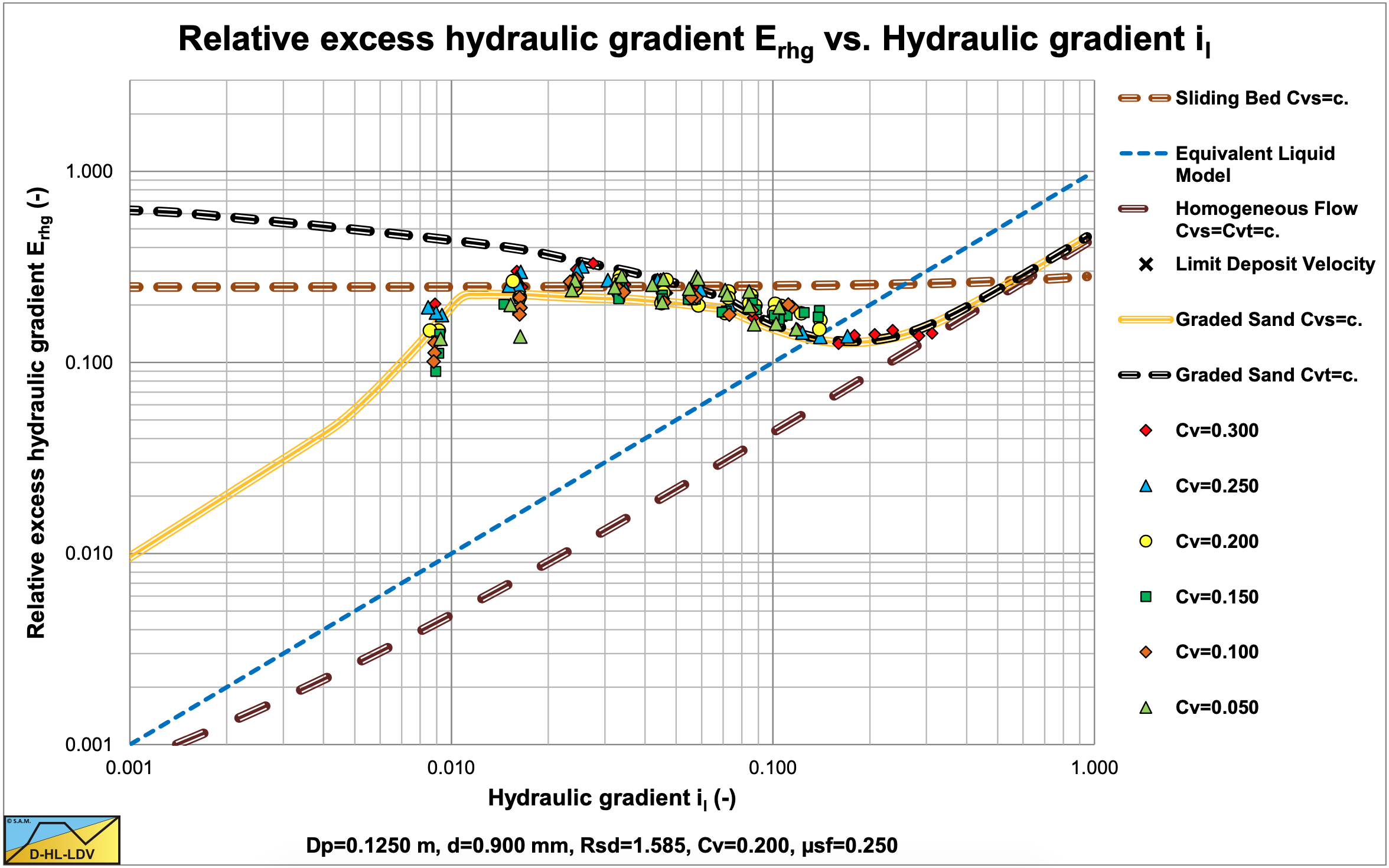
These experiments at constant Cvs, show a fixed bed to sliding bed to heterogeneous behavior. In both figures it is clear that the curve for graded sands match the data points better. The effect of the grading is different for different particle sizes.
7.2.5.4 R2, R3: Sliding Bed & Sliding Flow, Constant Cvt
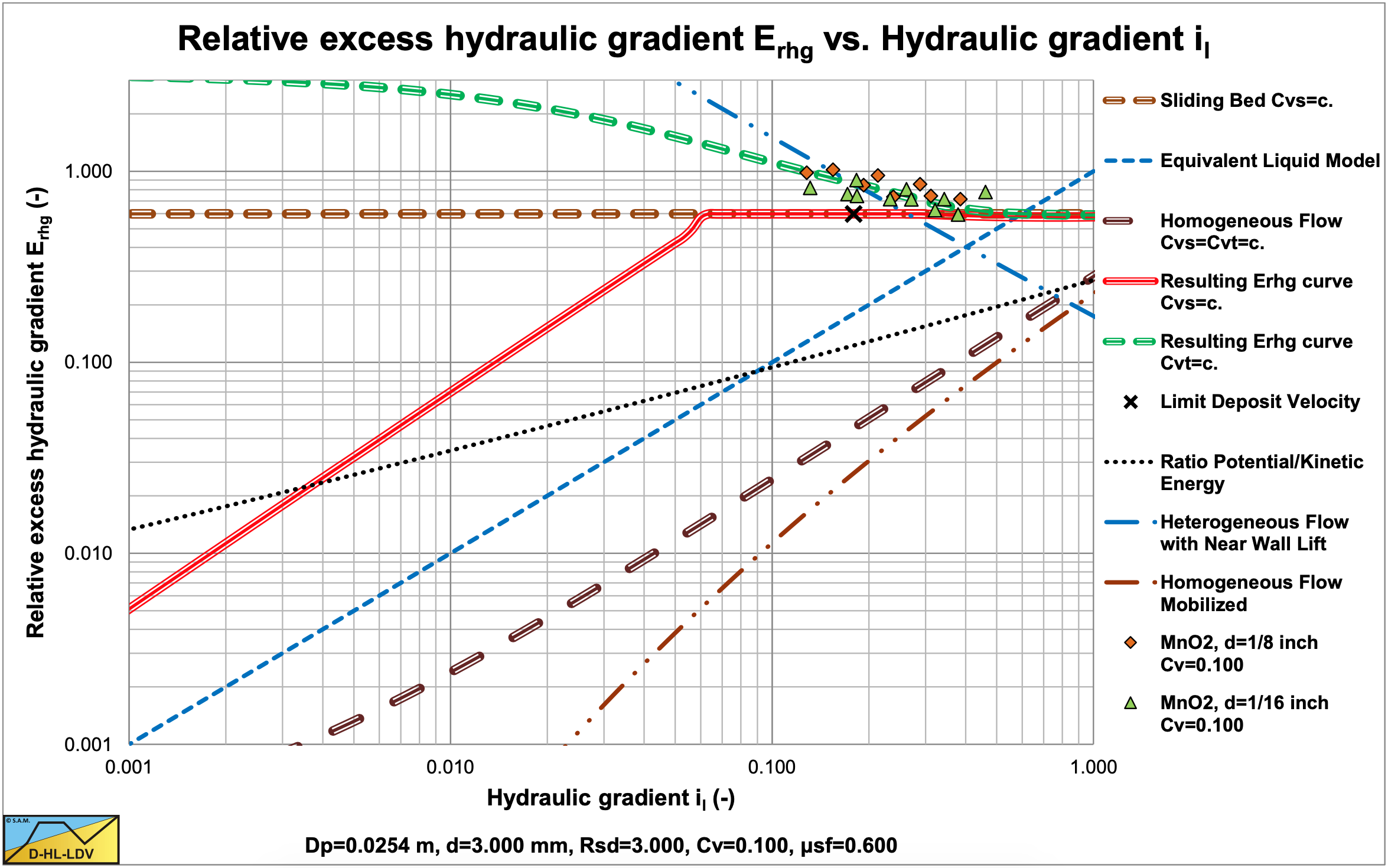
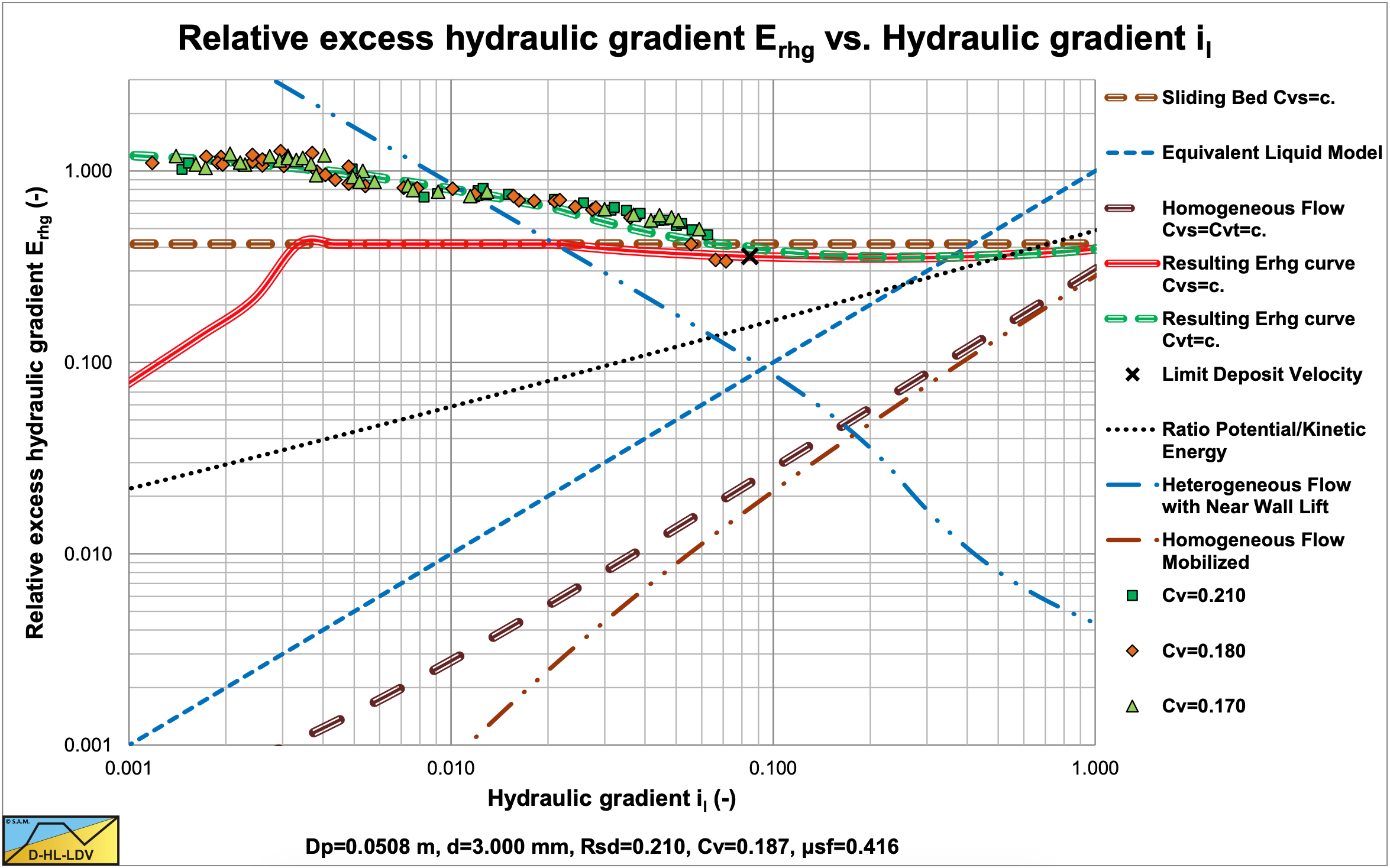
These experiments show the constant Cvt behavior at small line speeds, with a sliding/fixed bed and sliding flow behavior. The DHLLDV Framework gives a good prediction for both heavy (MnO2) and light (Acetal) solids.
7.2.5.5 L1, R1, L2, R2:, Homogeneous
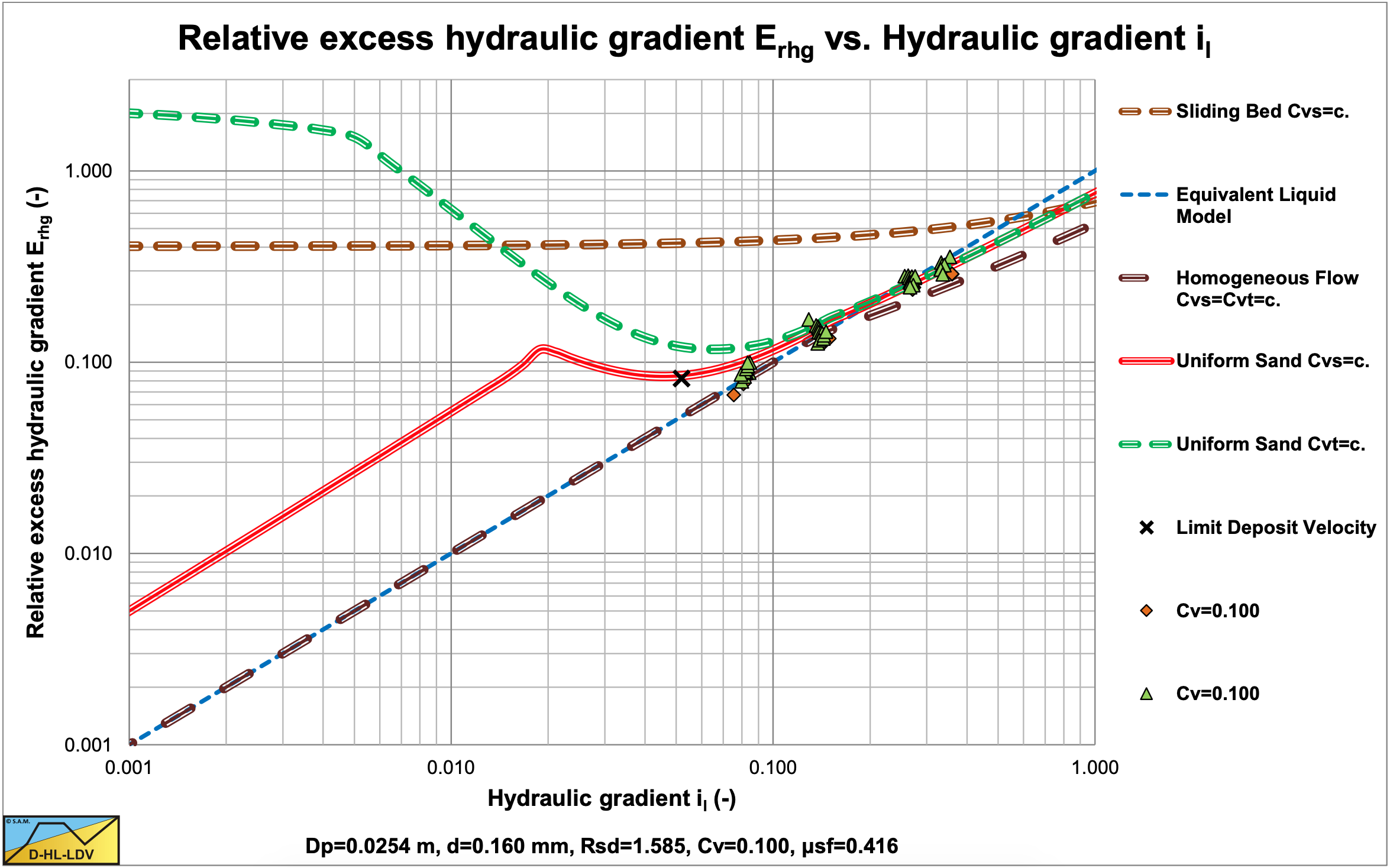
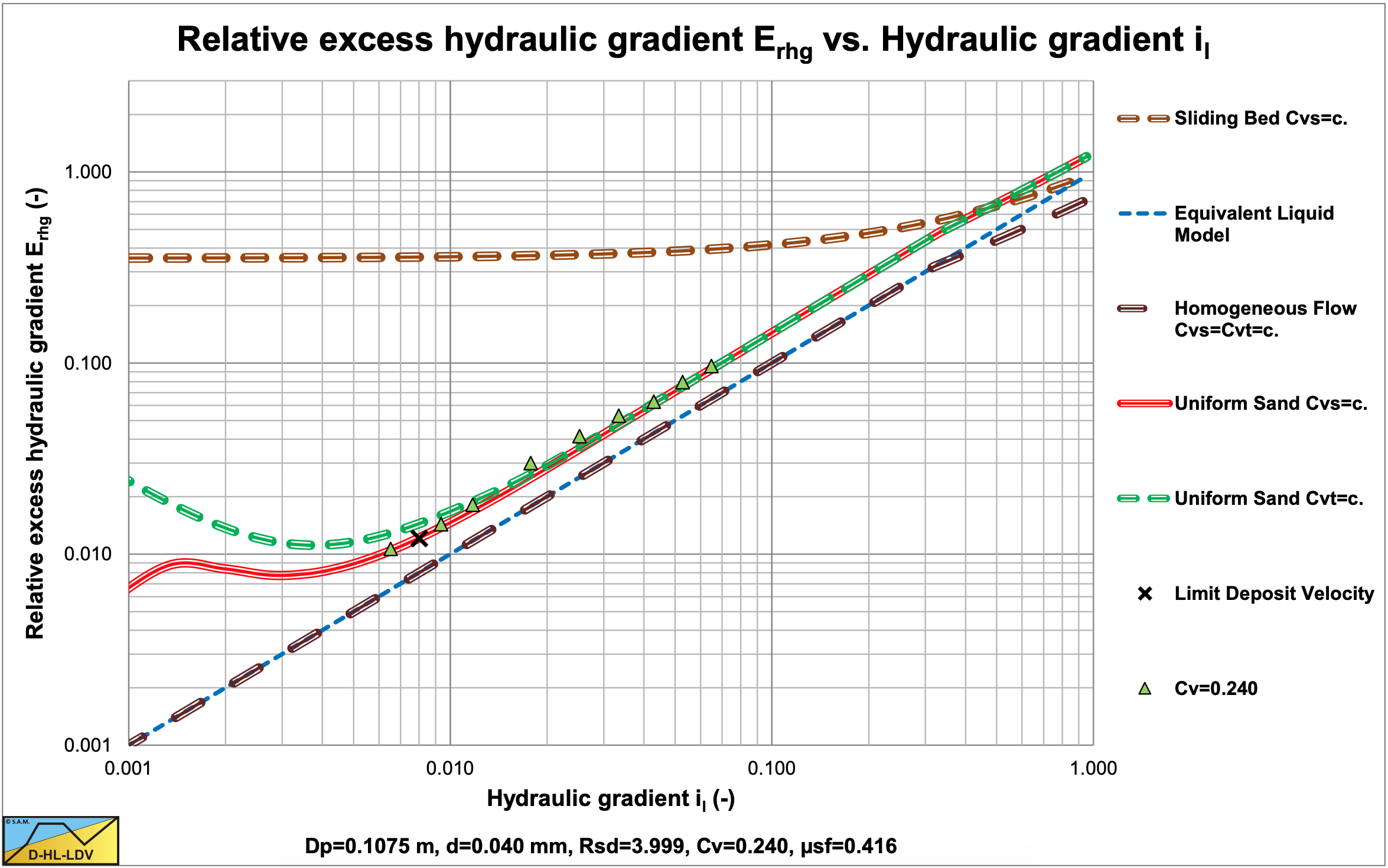
These experiments show homogeneous behavior, which occurs with small particles at relatively high line speeds. The Thomas (1976) graph also includes Thomas (1965) viscosity for very small particles.
7.2.5.6 L3, R3: Sliding Bed & Sliding Flow, Constant Cvs
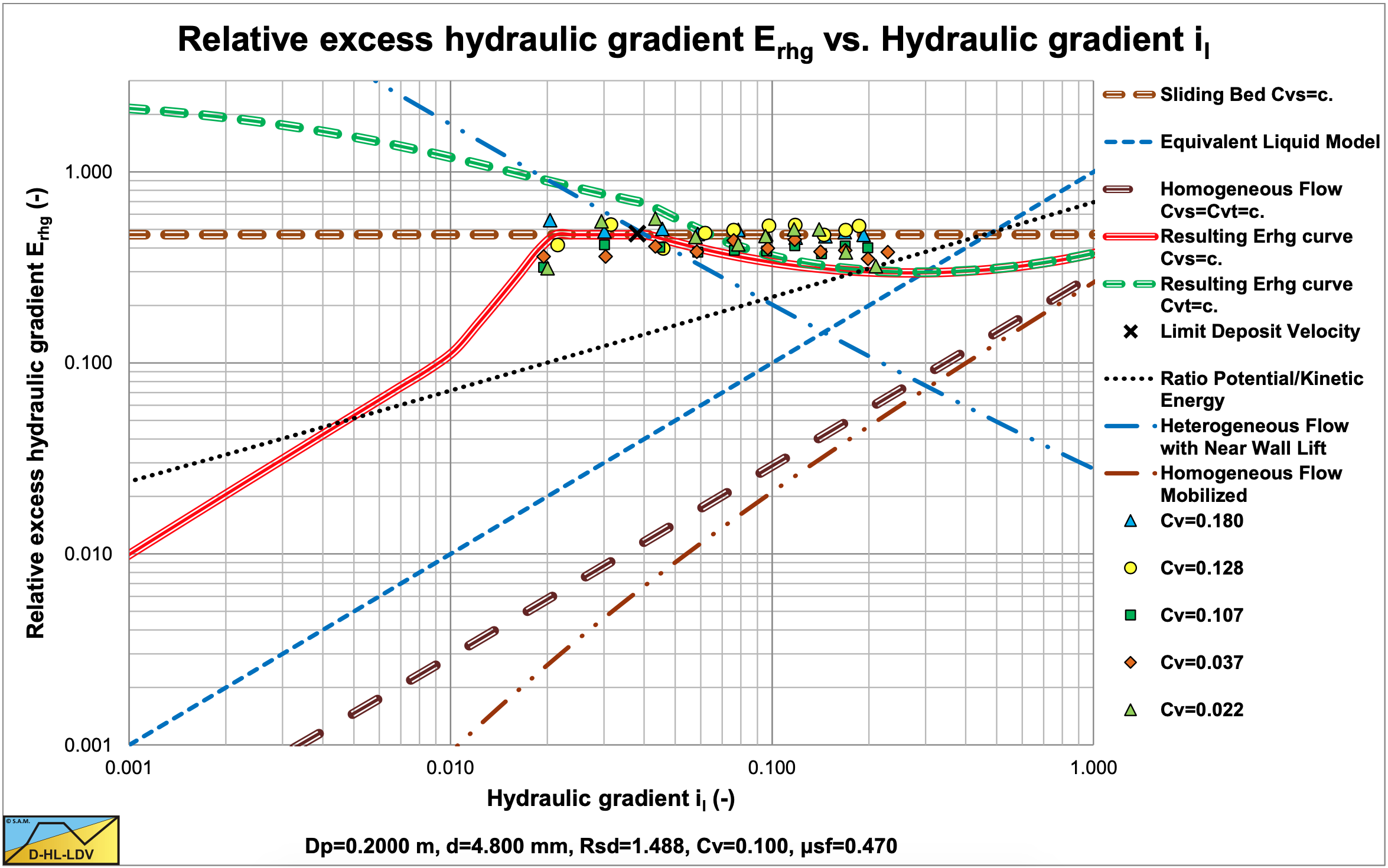
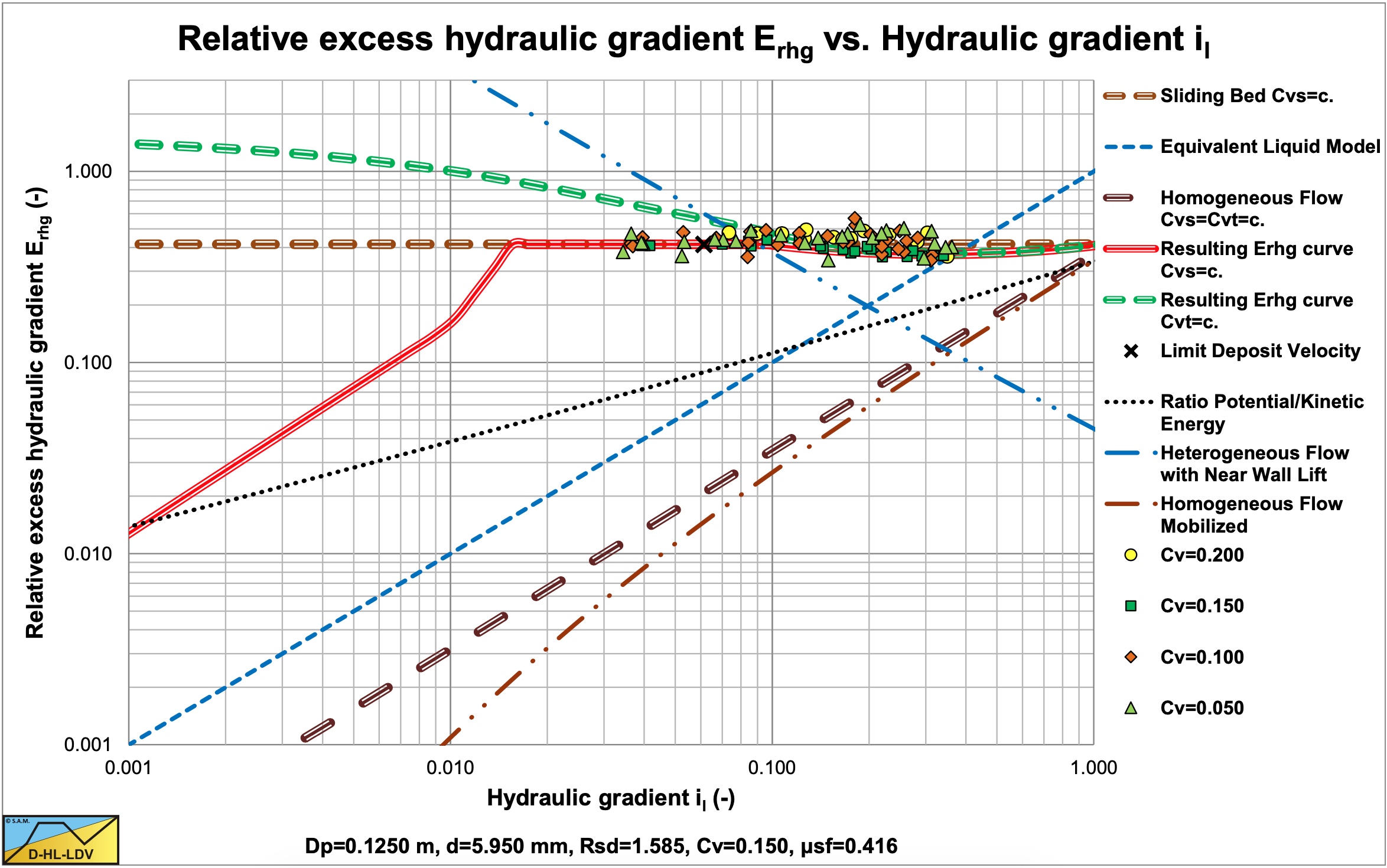
These experiments show the sliding bed and sliding flow regimes. Beyond the intersection point between a sliding bed and heterogeneous flow, the sliding flow curve is followed.
7.2.6 Discussion & Conclusions
The experimental graphs are given without a lot of explanation, because they should speak for themselves. These graphs show the different flow regimes and sometimes more than one flow regime. In general there is a lot of scatter. This is caused by the way experiments were carried out and specifically the accuracy of the concentration measurements. Sometimes concentrations within a certain bandwidth (for example 10-15%) are given with an average mentioned on the graph (for example 12.5%). But in spite of the scatter, the graphs clearly show the different regimes.
From these graphs and the regime and scenario definitions, it should be clear that experiments carried out in very small pipelines, like 1 inch diameter pipelines, can never be compared with experiments in very large pipelines, like 1 m diameter pipelines. In a 1 m diameter pipeline it is difficult to get a sliding bed regime, while in a 1 inch diameter pipeline it is very difficult not to get a sliding bed regime, due to the high hydraulic gradients. It is like comparing laminar and turbulent flow.
Each regime has its own physical and mathematical model. The fixed bed regime can be modeled with flow through a restricted cross section using the Televantos (1979) method for determining the friction factor. The sliding bed regime and partly the sliding flow regime can be modeled using the Newitt et al. (1955) method, with the appropriate friction factor (0.35-0.7). The heterogeneous regime can be modeled with one of the existing equations or with the Miedema et al. (2013) model. The homogeneous regime can be modeled using the equivalent liquid model, using 100% of the solids or for example using 60% of the solids, like some authors do. For the fixed bed/sliding bed regimes below the Limit Deposit Velocity, a 2 layer or 3 layer model can be used, but the Durand & Condolios (1952) approach, considering a flow Froude number which is equal to the flow Froude number at the Limit Deposit Velocity, also gives good results.
Just carrying out some curve fits and drawing conclusions is very dangerous, because the experiments may cover 2 or more regimes. For example, if 50% of the experiments are in the heterogeneous regime and 50% of the experiments are in the homogeneous regime, a curve fit would give a horizontal line in the Erhg(il) graph. If we look at experiments where 50% is in the fixed bed regime (constant Cvs) and 50% is in the heterogeneous regime (for example Figure 7.2-8 & Figure 7.2-12), the result of a curve fit is also a horizontal line. The cases however are completely different.
Recognizing the different regimes and especially the transitions between the different regimes is crucial in understanding what is physically happening.
The DHLLDV Framework gives a good match with most of the experiments shown here. In this book many more experiments are shown, usually compared to the DHLLDV Framework. The DHLLDV Framework gives good results for fine sands up to fine gravel in small to large pipes, compared to the experiments. For very coarse particles however still more research is required.
7.2.7 Nomenclature Flow Regimes & Scenario’s
|
A2 |
Cross section of the bed in the pipe |
m2 |
|
A1 |
Cross section of the mixture in suspension above the bed |
m2 |
|
A, Ap |
Cross section of the pipe |
m2 |
|
A2 |
Cross section of the solids in the pipe |
m2 |
|
Cv |
Volumetric concentration |
- |
|
Cvs |
Volumetric spatial concentration |
- |
|
Cvs,s |
Volumetric spatial concentration of the mixture in suspension above a fixed or sliding bed |
- |
|
Cvt |
Volumetric transport (delivered) concentration |
- |
|
d |
Particle diameter |
mm |
|
d50 |
Median particle diameter - 50% by weight is smaller |
mm |
|
Dp |
Pipe diameter |
m |
|
Erhg |
Relative Excess Hydraulic Gradient |
- |
|
im |
Mixture head loss |
m/m |
|
il |
Liquid hydraulic gradient |
m/m |
|
iw |
Water hydraulic gradient |
m/m |
|
n |
Porosity |
- |
|
O1 |
Circumference liquid-pipe wall |
m |
|
O2 |
Circumference bed-pipe wall |
m |
|
O12 |
Width liquid-bed interface |
m |
| \(\ \mathrm{Q}_{\mathrm{m}} \text{ or } \dot{\mathrm{V}}_{\mathrm{m}}\) |
Flow rate of mixture |
m3/s |
| \(\ \mathrm{Q}_{\mathrm{s}}\text{ or }\dot{\mathrm{V}}_{\mathrm{s}}\) |
Flow rate of solids |
m3/s |
|
Rsd |
Relative submerged density |
- |
|
R |
Stratification ratio Wilson |
- |
|
Srs |
Slip Relative Squared or Stratification Ratio Solids |
- |
|
Shr |
Settling velocity Hindered Relative |
- |
|
vls |
Velocity of the slurry, line speed |
m/s |
|
vls,e |
Effective line speed. Line speed above the fixed or moving bed. |
m/s |
|
vm |
Velocity of the slurry, line speed (same as vls) |
m/s |
|
vs |
Average velocity of the solids |
m/s |
|
vsl |
Slip velocity of the solids relative to the mixture |
m/s |
|
Vb |
Volume of the bed |
m3 |
|
Vcl |
Volume of the closed loop |
m3 |
|
Vm |
Volume of the mixture in a pipe |
m3 |
|
Vm,s |
Volume of the mixture in suspension above the bed |
m3 |
|
Vs |
Volume of the solids in a pipe |
m3 |
|
Vs,s |
Volume of the solids in suspension above the bed |
m3 |
|
vt |
Terminal settling velocity of the particles |
m/s |
|
β |
Richardson & Zaki hindered settling power |
- |
|
λ1 |
Darcy-Weisbach friction factor between liquid and pipe wall |
- |
|
λ2 |
Darcy-Weisbach friction factor between liquid and pipe wall in bed |
- |
|
λ22 |
Darcy-Weisbach friction factor between liquid and bed |
- |
|
κC |
Concentration eccentricity factor. |
- |
|
μsf |
Friction coefficient for a sliding bed |
- |
|
ρl, ρw |
Density of the liquid |
ton/ m3 |
|
ρm |
Density of the mixture |
ton/ m3 |
|
ρs |
Density of the solids |
ton/ m3 |


