6.6: Numerical Water Pore Pressure Calculations
- Page ID
- 29455
The water under-pressures in the sand package on and around the blade are numerically determined using the finite element method. The solution of such a calculation is however not only dependent on the physical model of the problem, but also on the next points:
-
The size of the area in which the calculation takes place.
-
The size and distribution of the elements.
-
The boundary conditions.
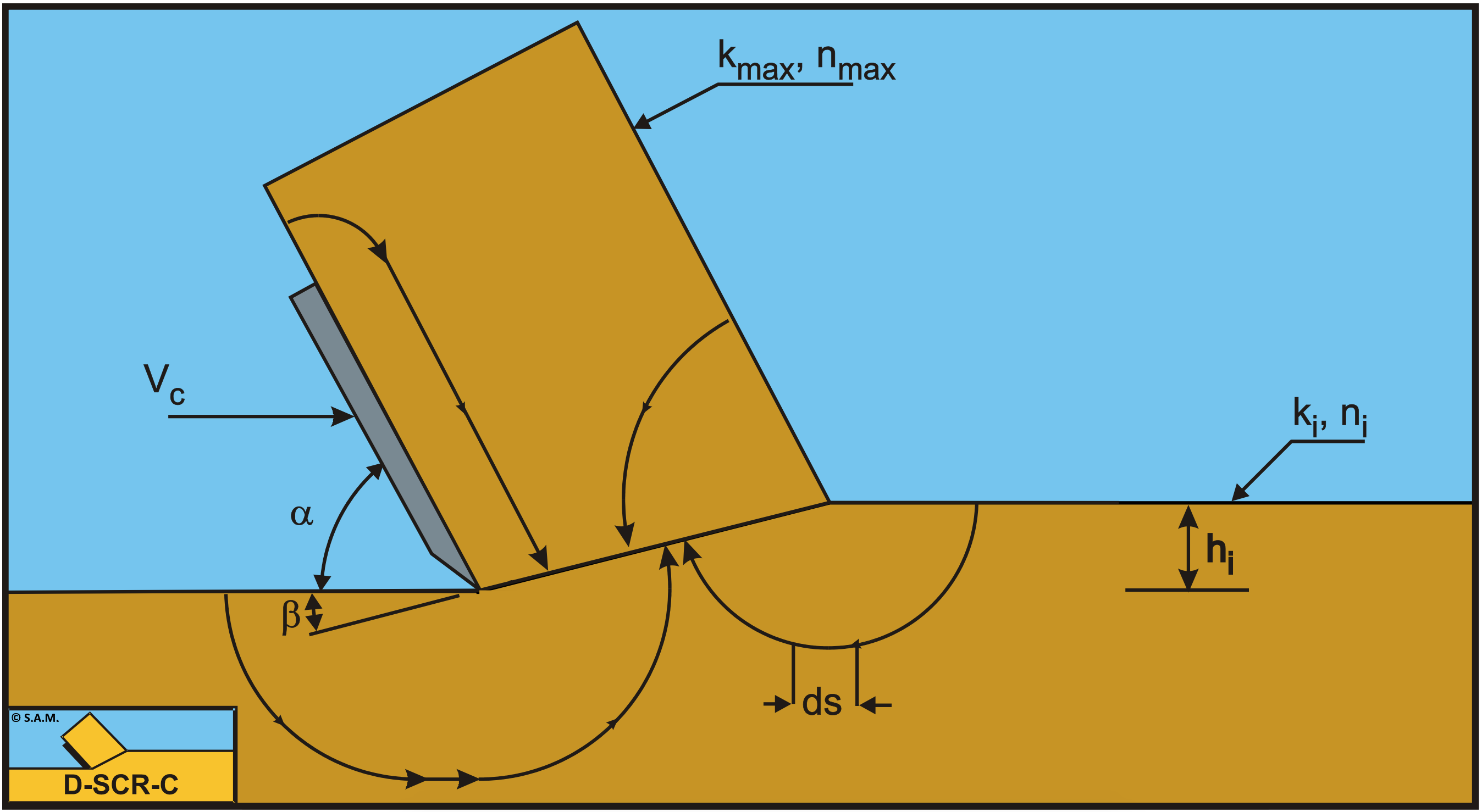
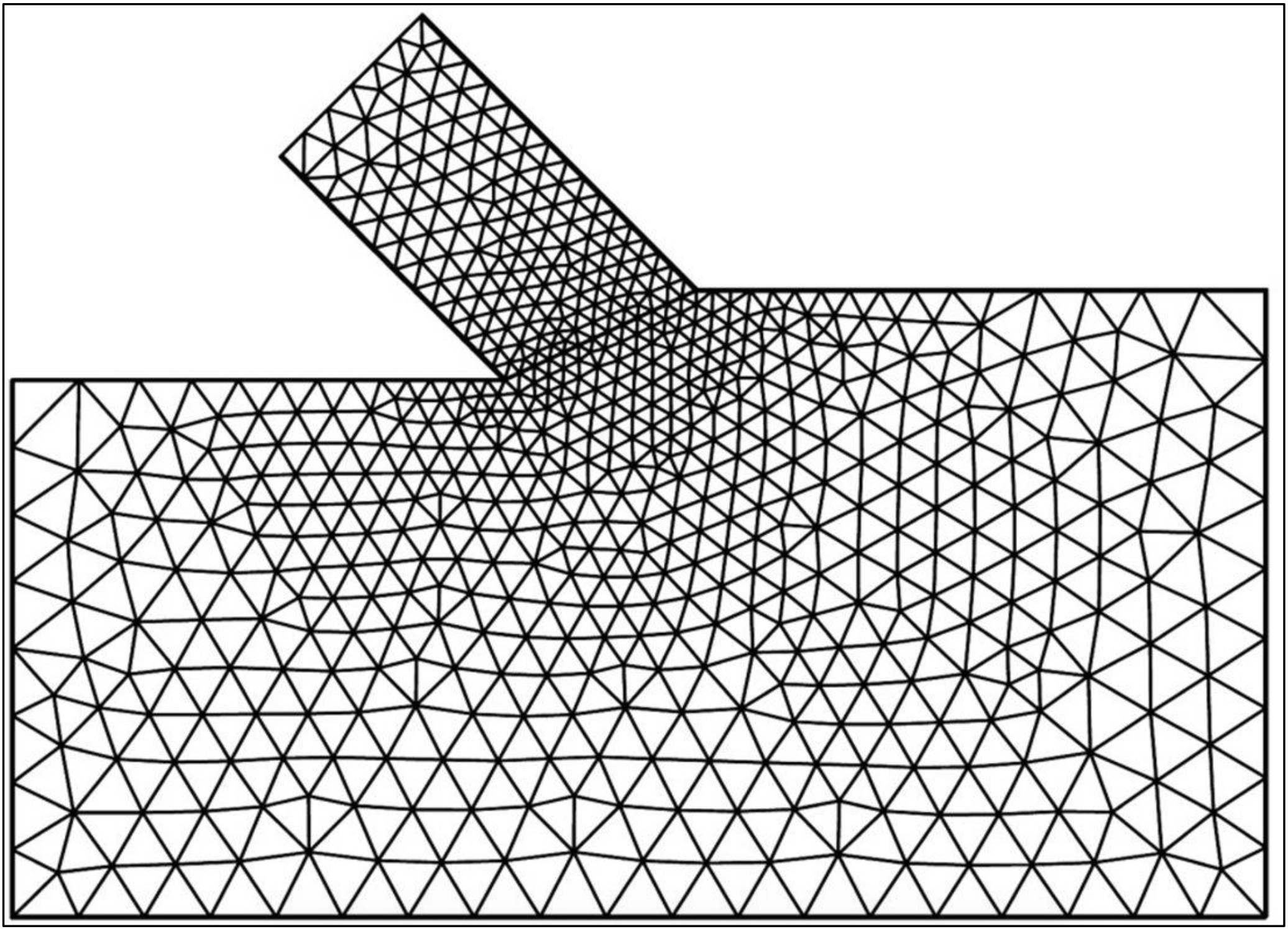
The choices for these three points have to be evaluated with the problem that has to be solved in mind. These calculations are about the values and distribution of the water under-pressures in the shear zone and on the blade. A variation of the values for point 1 and 2 may therefore not influence this part of the solution. This is achieved by on the one hand increasing the area in which the calculations take place in steps and on the other hand by decreasing the element size until the variation in the solution was less than 1%. The distribution of the elements is chosen such that a finer mesh is present around the blade tip, the shear zone and on the blade, also because of the blade tip problem. A number of boundary conditions follow from the physical model of the cutting process, these are:
-
The boundary condition in the shear zone. This is described by equation (6-23).
-
The boundary condition along the free sand surface. The hydrostatic pressure at which the process takes place, can be chosen, when neglecting the dimensions of the blade and the layer in relation to the hydrostatic pressure head. Because these calculations are meant to obtain the difference between the water under-pressures and the hydrostatic pressure it is valid to take a zero pressure as the boundary condition.
The boundary conditions, along the boundaries of the area where the calculation takes place that are located in the sand package are not determined by the physical process. For this boundary condition there is a choice between:
-
A hydrostatic pressure along the boundary.
-
A boundary as an impenetrable wall.
-
A combination of a known pressure and a known specific flow rate.
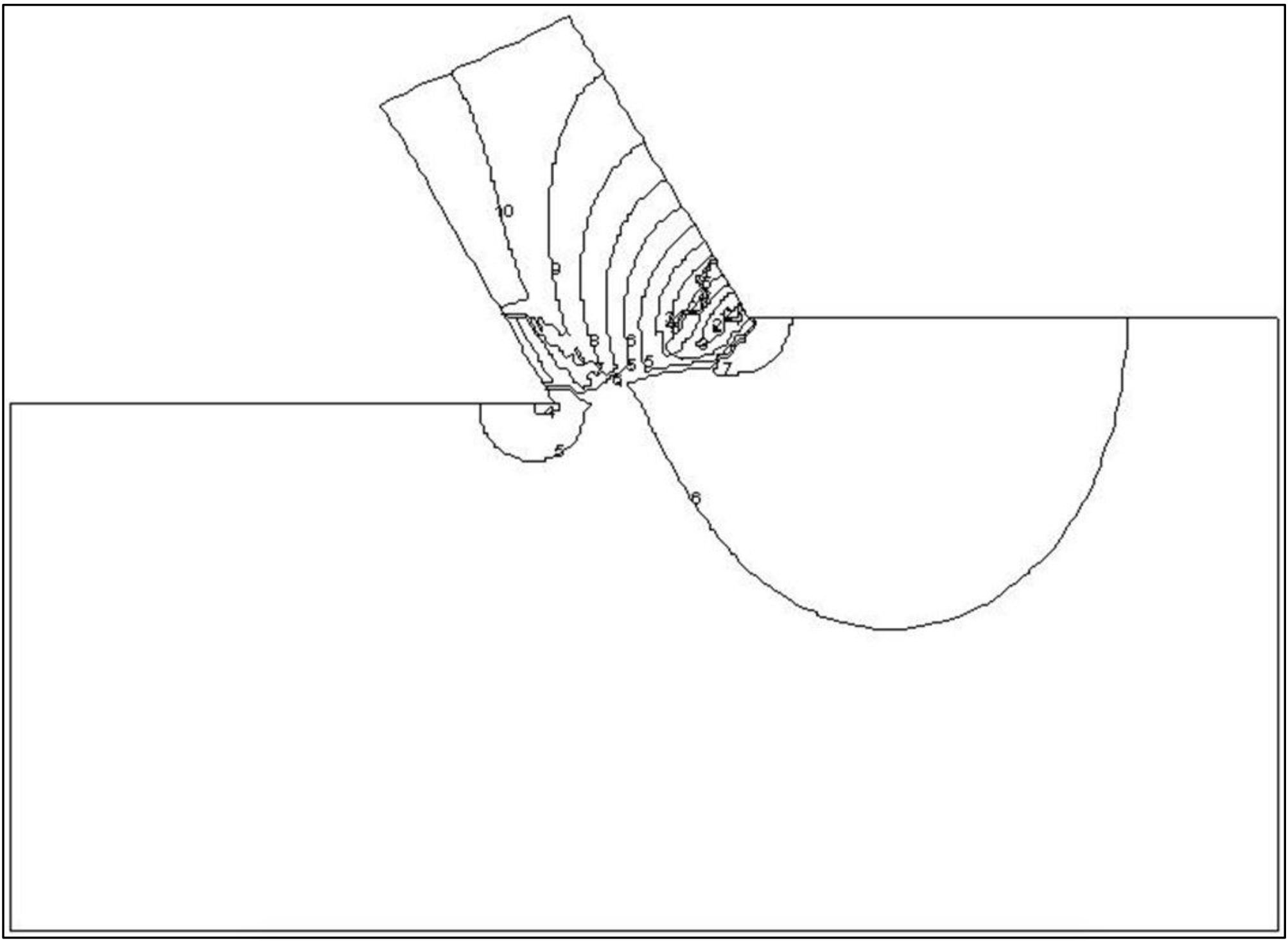
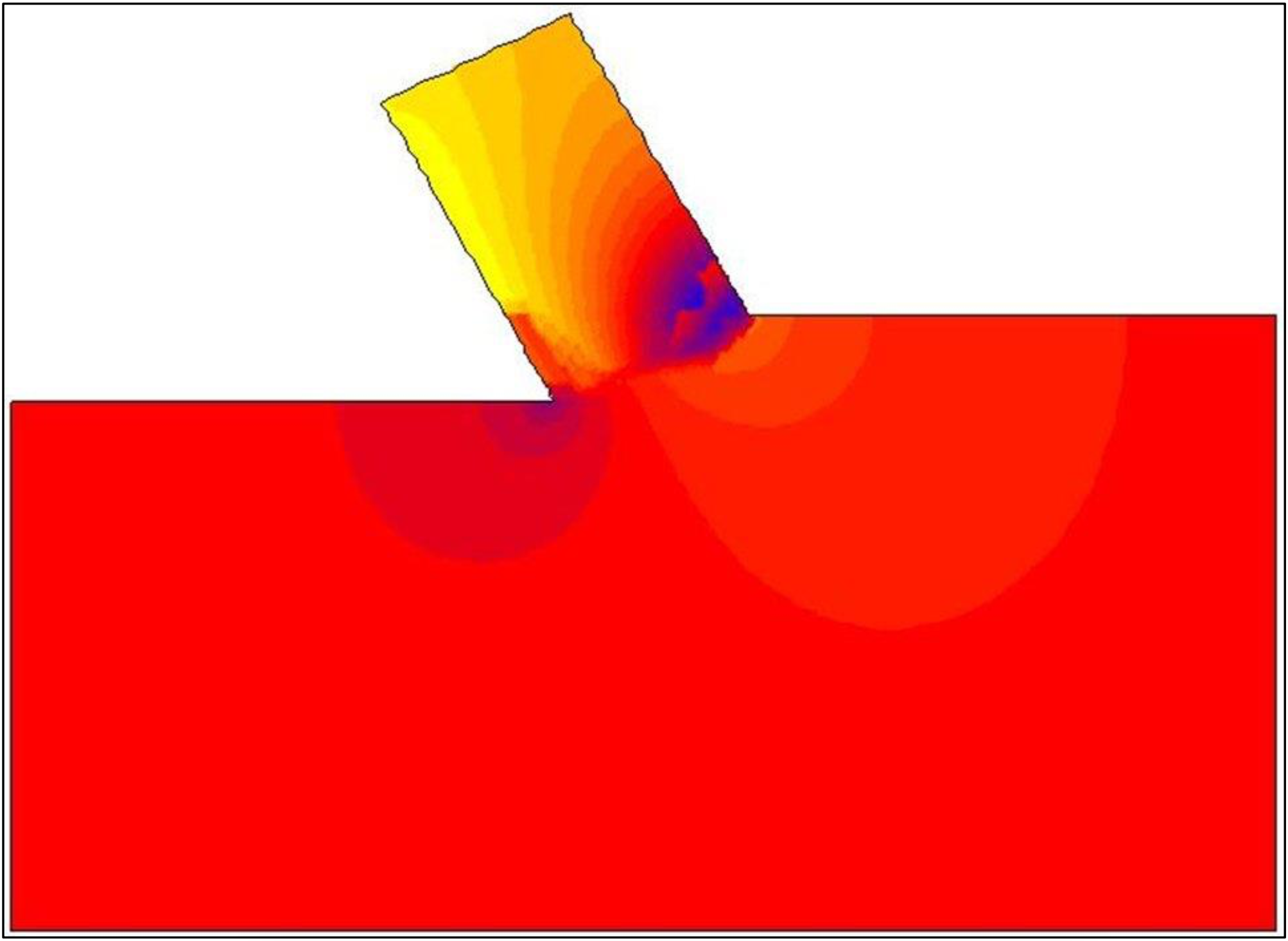
None of these choices complies with the real process. Water from outside the calculation area will flow through the boundary. This also implies, however, that the pressure along this boundary is not hydrostatic. If, however, the boundary is chosen with enough distance from the real cutting process the boundary condition may not have an influence on the solution. The impenetrable wall is chosen although this choice is arbitrary. Figure 6-8 gives an impression of the size of the area and the boundary conditions, while Figure 6-10 shows the element mesh. Figure 6-12 shows the two-dimensional distribution of the water under-pressures. A table with the dimensionless pore pressures can be found in Miedema (1987 September), Miedema & Yi (2001) and in Appendix C: and Appendix R:
The following figures give an impression of how the FEM calculations are carried out:
Figure 6-10 and Figure 6-11: Show how the mesh has been varied in order to get a 1% accuracy.
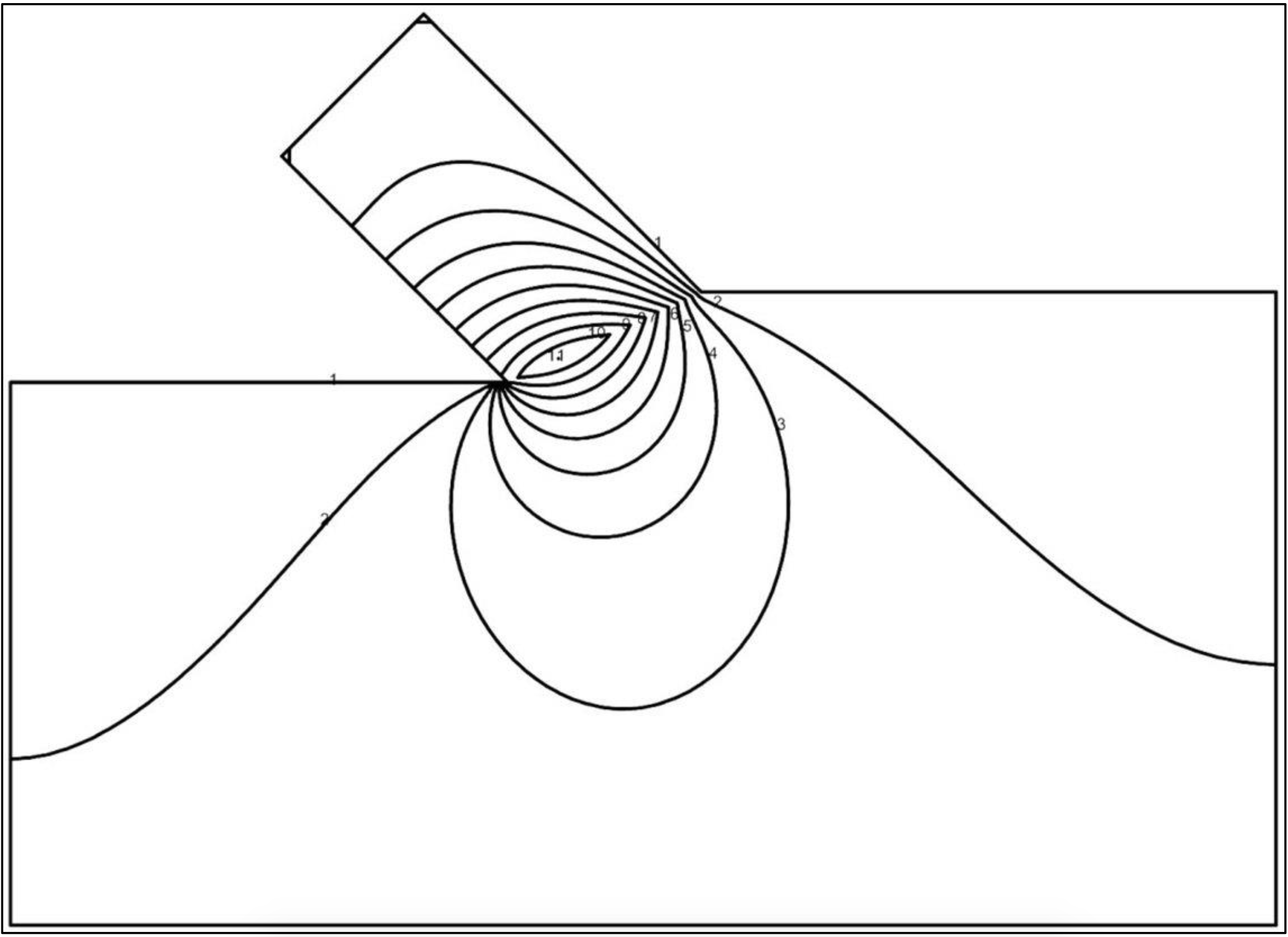
Figure 6-12: Shows both the equipotential lines and the flow lines (stream function).
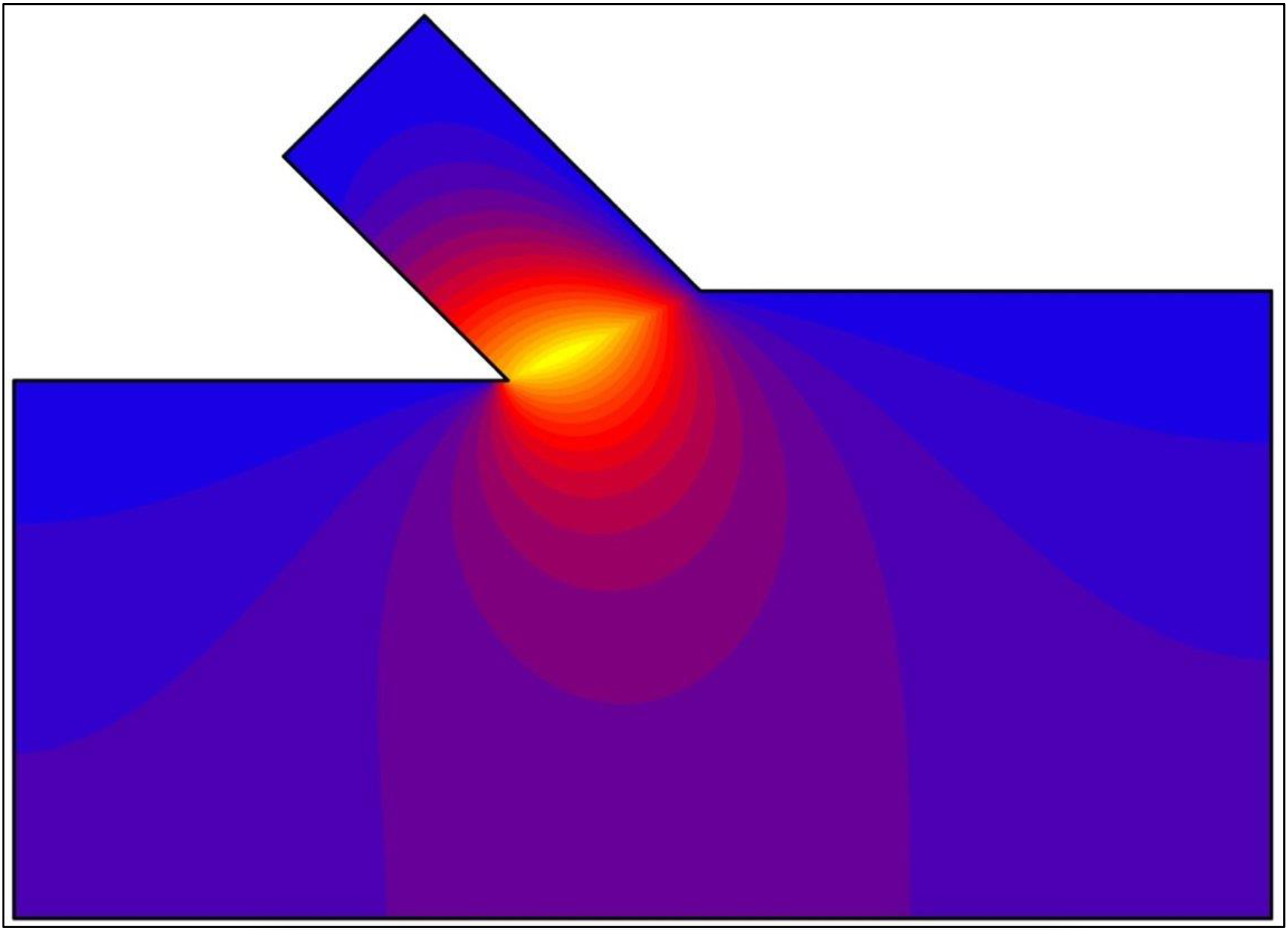
Figure 6-14 and Figure 6-15: Show the equipotential lines both as lines and as a color plot. This shows clearly where the largest under pressures occur on the shear plane.
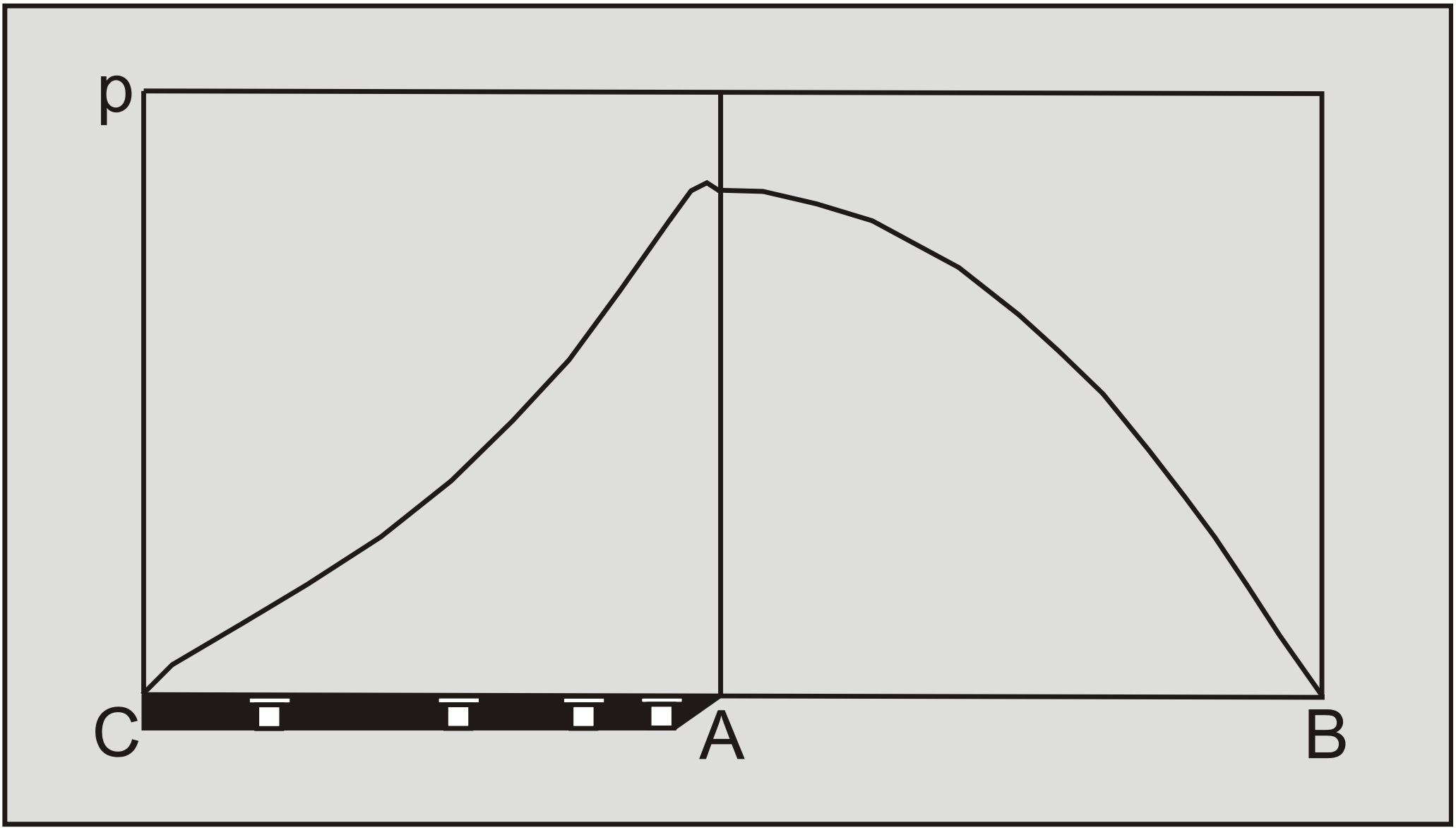
Figure 6-13 shows the pressure distribution on both the shear plane and the blade. From these pressure distributions the average dimensionless pressures p1m and p2m are determined.
Figure 6-16 and Figure 6-17: Show the streamlines both as lines and as a color plot. This shows the paths of the pore water flow.