6.10: The Coefficients a1 and a2

In the derivation of the calculation of the water under-pressures around the blade for the non-cavitating cutting process, resulting in equations (6-30) and (6-31), it already showed that the water under-pressures are determined by the permeability of the undisturbed sand k_i and the permeability of the disturbed sand k_max. Equation (6-25) shows this dependence. The water under-pressures are determined for several ratios of the initial permeability of the undisturbed sand to the maximum permeability of the disturbed sand:

k_i/k_max = 1

k_i/k_max = 0.5

k_i/k_max = 0.25

The average water under-pressures p_1m and p_2m can be put against the ratio k_i/k_max, for a certain shear angle β. A hyperbolic relation emerges between the average water under-pressures and the ratio of the permeabilities. If the reciprocal values of the average water under-pressures are put against the ratio of the permeabilities a linear relation emerges.

The derivatives of p_1m and p_2m to the ratio k_i/k_max are, however, not equal to each other. This implies that a relation for the forces as a function of the ratio of permeabilities cannot be directly derived from the found average water under-pressures.

This is in contrast with the method used by Van Leussen and Van Os (1987 December). They assume that the average pore pressure on the blade has the same dependability on the ratio of permeabilities as the average pore pressure in the shear zone. No mathematical background is given for this assumption.

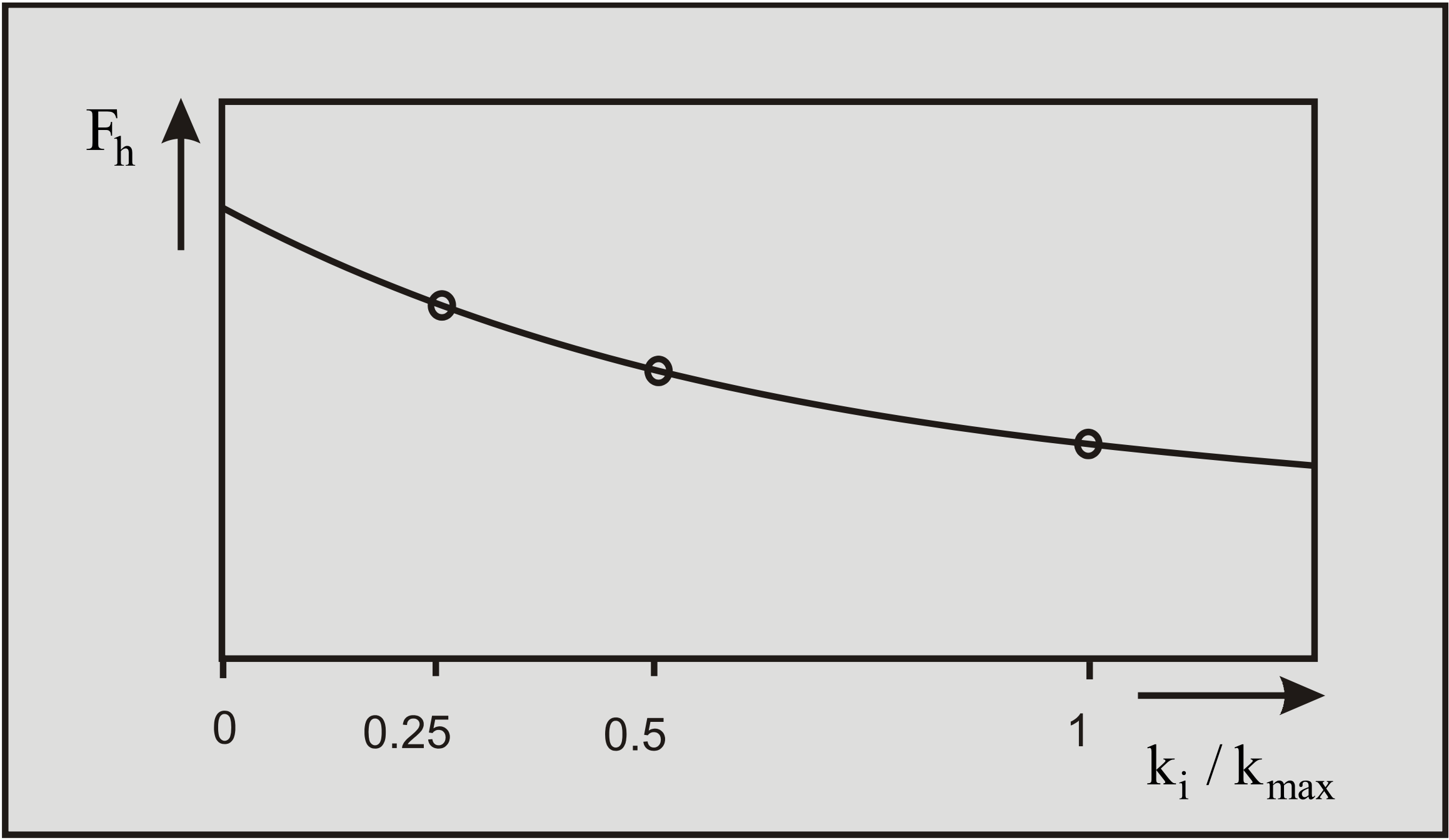
For the several ratios of the permeabilities it is possible with the shear angles determined, to determine the dimensionless forces F_h and F_v. If these dimensionless forces are put against the ratio of the permeabilities, also a hyperbolic relation is found (Miedema (1987 September)), shown in Figure 6-26 and Figure 6-27.
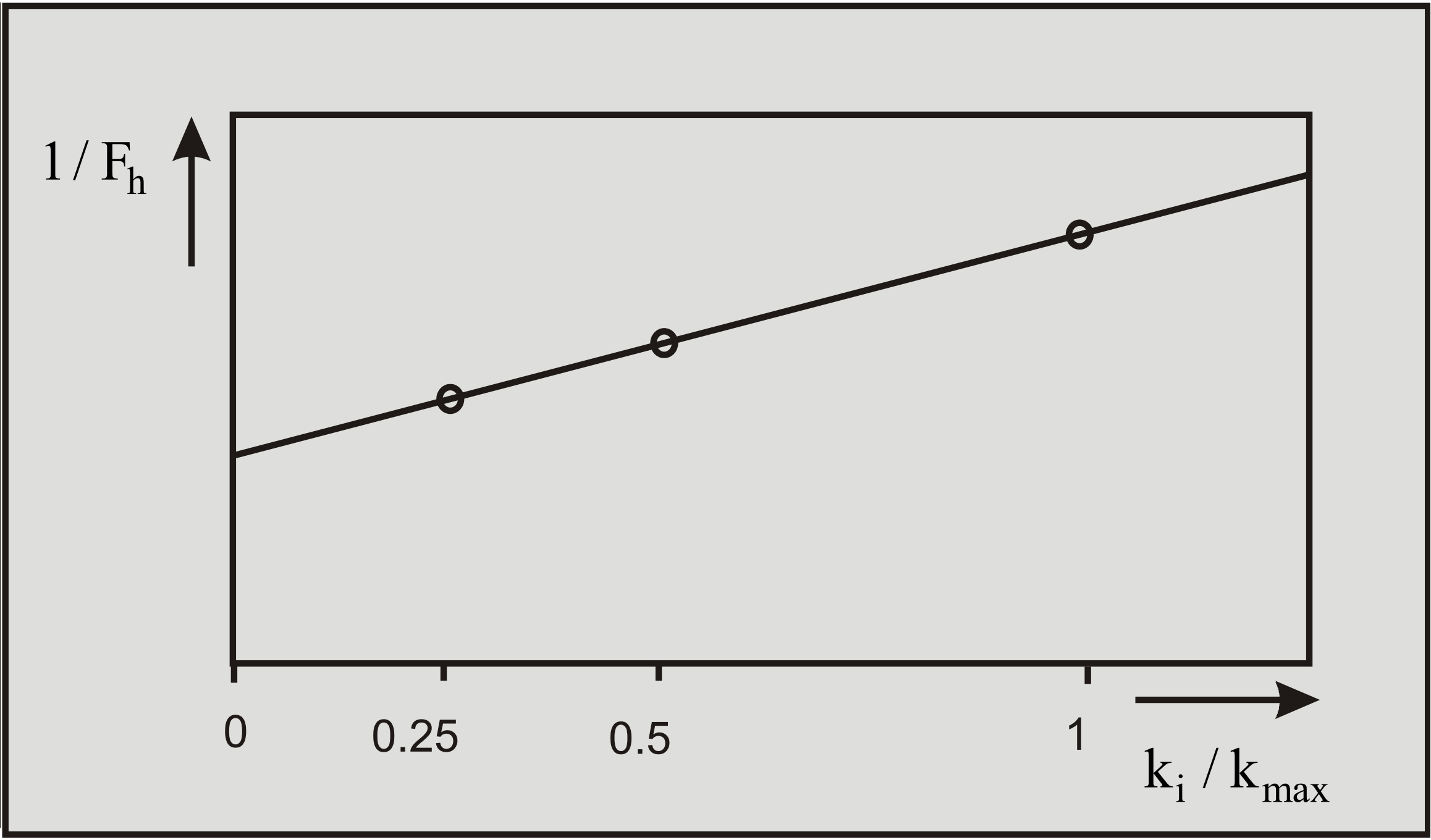
A linear relation can therefore also be found if the reciprocal values of the dimensionless forces are taken. This relation can be represented by:

\[\ \frac{1}{\mathrm{F}_{\mathrm{h}}}=\mathrm{a}+\mathrm{b} \cdot \frac{\mathrm{k}_{\mathrm{i}}}{\mathrm{k}_{\mathrm{m a x}}}\tag{6-68}\]

With the next transformations an equation can be derived for a weighted average permeability k_m:

\[\ \mathrm{a_{1}=\frac{b}{a+b} \quad\& \quad a_{2}=\frac{a}{a+b}}\tag{6-69}\]

So:

\[\ \mathrm{k}_{\mathrm{m}}=\mathrm{a}_{\mathrm{1}} \cdot \mathrm{k}_{\mathrm{i}}+\mathrm{a}_{2} \cdot \mathrm{k}_{\mathrm{m a x}}\quad\text{ with: }\quad\mathrm{a}_{1}+\mathrm{a}_{2}=\mathrm{1}\tag{6-70}\]

Since the sum of the coefficients a₁ and a₂ is equal to 1 only coefficient a₁ is given in Miedema (1987) and 0. It also has to be remarked that this coefficient is determined on the basis of the linear relation of F_h (dimensionless c₁), because the horizontal force gives more or less the same relation as the vertical force, but has besides a much higher value. Only for the 60^o blade, where the vertical force is very small and can change direction, differences occur between the linear relations of the horizontal and the vertical force as function of the ratio of the permeabilities.

The influence of the undisturbed soil increases when the blade-height/layer-thickness ratio increases. This can be explained by the fact that the water that flows to the shear zone over the blade has to cover a larger distance with an increasing blade height and therefore has to overcome a higher resistance. Relatively more water will have to flow through the undisturbed sand to the shear zone with an increasing blade height.

Figure 6-26: The force F_h as function of the ratio between k_i and k_max.

Figure 6-27: The reciprocal of the force F_h as function of the ratio between k_i and k_max.