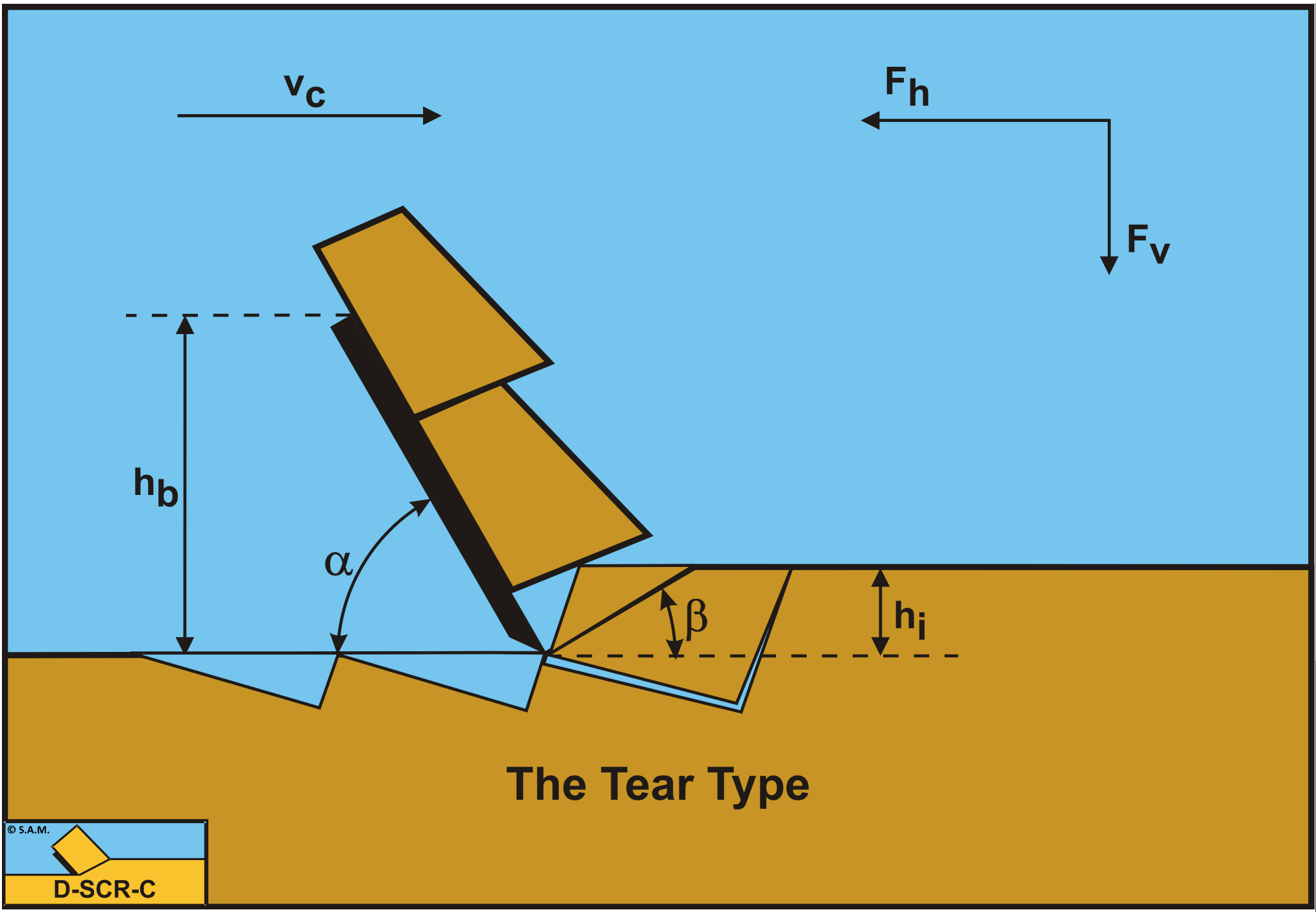
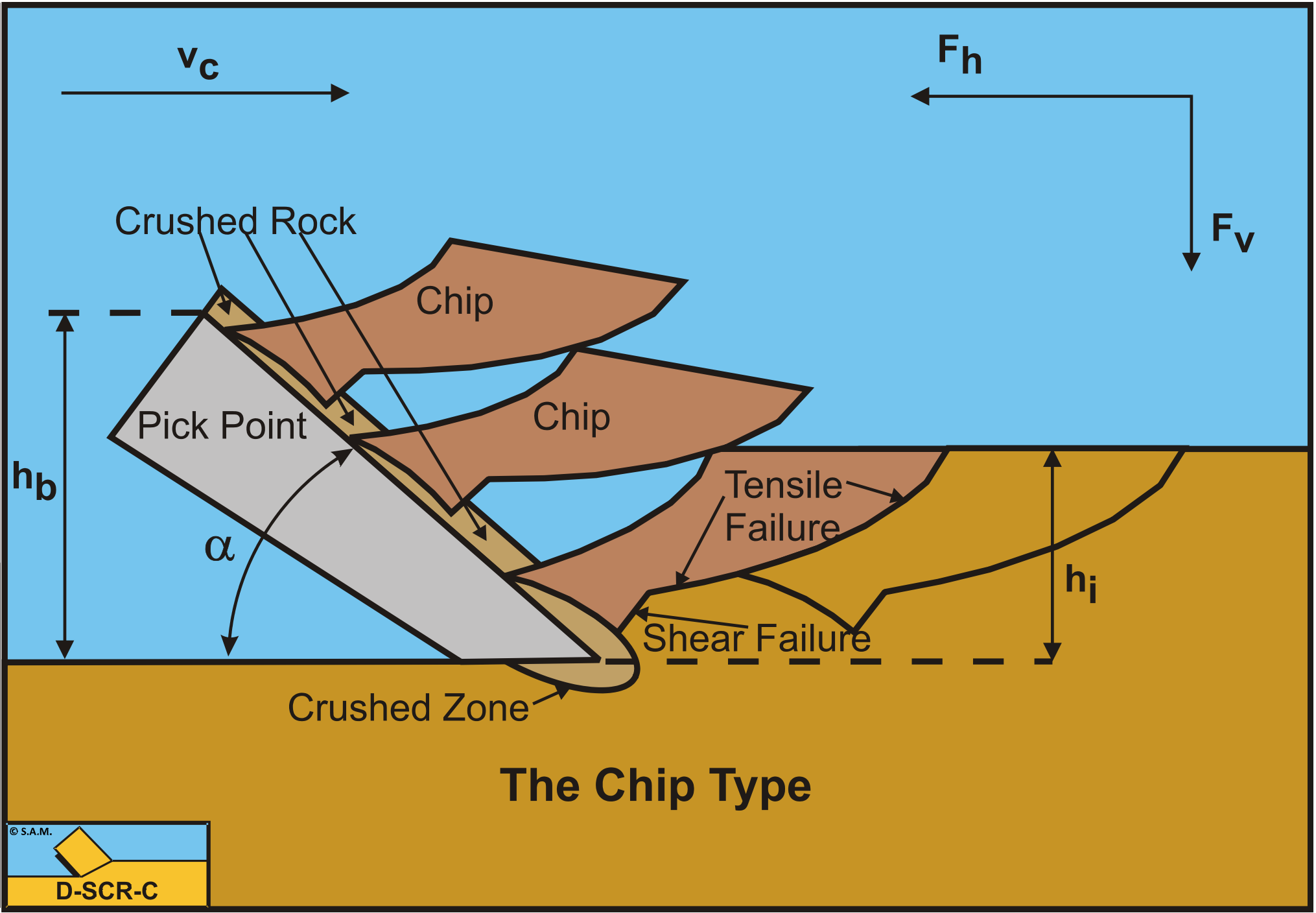
9.3: The Tear Type and the Chip Type
- Page ID
- 29473
Similar to the derivation of equation (8-127) for the occurrence of tensile failure under atmospheric conditions, equation (9-19) can be derived for the occurrence of tensile failure under hyperbaric conditions. Under hyperbaric conditions equation (9-19) will almost always be true, because of the terms with r1 and r2 which may become very big (positive). So tensile failure will not be considered for hyperbaric conditions.
\[\ \mathrm{c}\cdot \left( \begin{array}{left}\mathrm{\frac{r\cdot \frac{\sin(\beta)\cdot\cos(\delta)}{\sin(\alpha)}+r_2\cdot\frac{\sin(\beta)\cdot sin(\delta)}{sin(\alpha)}}{sin(\alpha+\beta+\delta+\varphi)}}\\ \mathrm{+\frac{+r_1\cdot sin(\alpha+\beta+\delta)}{sin(\alpha+\beta+\delta+\varphi)} }\\ +\mathrm{\frac{-cos(\alpha+\beta+\delta)-sin(\alpha+\beta+\delta+\varphi)}{sin(\alpha+\beta+\delta+\varphi)}}\end{array} \right)\cdot\mathrm{\left(\frac{1-sin(\varphi)}{cos(\varphi)} \right)>\sigma_T}\tag{9-19} \]


