3.3: Ring lattice

Last updated
Save as PDF

Page ID: 46588

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure \(\PageIndex{1}\): A ring lattice with n=10 and k=4.

A regular graph is a graph where each node has the same number of neighbors; the number of neighbors is also called the degree of the node.

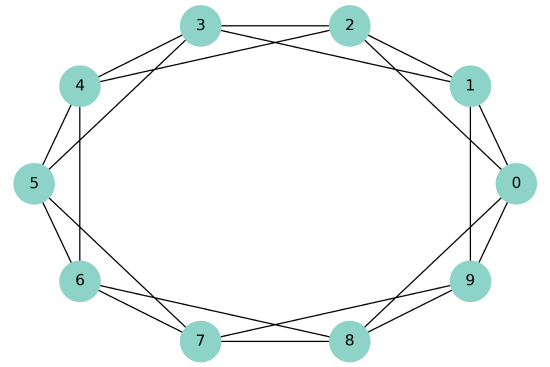
A ring lattice is a kind of regular graph, which Watts and Strogatz use as the basis of their model. In a ring lattice with n nodes, the nodes can be arranged in a circle with each node connected to the k nearest neighbors.

For example, a ring lattice with n=3 and k=2 would contain the following edges: (0, 1), (1, 2), and (2, 0). Notice that the edges “wrap around” from the highest-numbered node back to 0.

More generally, we can enumerate the edges like this:

def adjacent_edges(nodes, halfk): 
    n = len(nodes) 
    for i, u in enumerate(nodes): 
        for j in range(i+1, i+halfk+1): 
            v = nodes[j % n] 
            yield u, v

adjacent_edges takes a list of nodes and a parameter, halfk, which is half of k. It is a generator function that yields one edge at a time. It uses the modulus operator, %, to wrap around from the highest-numbered node to the lowest.

We can test it like this:

>>> nodes = range(3) 
>>> for edge in adjacent_edges(nodes, 1): 
...     print(edge) 
(0, 1) 
(1, 2) 
(2, 0)

Now we can use adjacent_edges to make a ring lattice:

def make_ring_lattice(n, k): 
    G = nx.Graph() 
    nodes = range(n) 
    G.add_nodes_from(nodes) 
    G.add_edges_from(adjacent_edges(nodes, k//2)) 
    return G

Notice that make_ring_lattice uses floor division to compute halfk, so it is only correct if k is even. If k is odd, floor division rounds down, so the result is a ring lattice with degree k-1. As one of the exercises at the end of the chapter, you will generate regular graphs with odd values of k.

We can test make_ring_lattice like this:

lattice = make_ring_lattice(10, 4)

Figure \(\PageIndex{1}\) shows the result.