11.4: Air Resistance

Last updated
Save as PDF

Page ID: 84742

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

To make this simulation more realistic, we can add air resistance. For large objects moving quickly through air, the force due to air resistance, called drag, is proportional to velocity squared. For an object falling down, drag is directed up, so if velocity is negative, drag force is positive.

Here’s how we can compute the force of drag as a function of velocity in one dimension:

\[f_\mathrm{d} = -\mathrm{sign}(v) b v^2\notag\]

where \(v\) is velocity and \(b\) is a drag constant that depends on the density of air, the cross-sectional area of the object, and the shape of the object.

The sign or signum function returns the value \(1\) for positive values of \(v\) and \(-1\) for negative values. So \(f_\mathrm{d}\) is always in the opposite direction of \(v\).

To convert from force to acceleration we have to know mass, but that’s easy to find: the mass of a penny is about 2.5 g. It’s not as easy to find the drag constant, but based on reports that the terminal velocity of a penny is about 18 m/s, I’ve estimated that it’s about 75e-6 kg/m.

Listing 11.2 defines a function that takes t and X as input variables and returns the total acceleration of the penny due to gravity and drag:

Listing 11.2: Calculating acceleration of a penny with drag

function res = acceleration(t, X)
    b = 75e-6;                 % drag constant in kg/m
    v = X(2);                  % velocity in m/s
    f_d = -sign(v) * b * v^2;  % drag force in N

    m = 2.5e-3;               % mass in kg
    a_d = f_d / m;            % drag acceleration in m/s^2

    a_g = -9.8;               % acceleration of gravity in m/s^2
    res = a_g + a_d;          % total acceleration
end

First, we compute force due to drag. Then we compute acceleration due to drag. Lastly, we compute total acceleration due to drag and gravity.

Be careful when you’re working with forces and accelerations; make sure you only add forces to forces or accelerations to accelerations. In my code, I use comments to remind myself what units the values have. That helps me avoid errors like adding forces to accelerations.

To use this function, we make a small change in rate_func:

function res = rate_func(t, X)
    y = X(1);
    v = X(2);

    dydt = v;
    dvdt = acceleration(t, X);   % this line has changed

    res = [dydt; dvdt];
end

In the previous version, dvdt is always -9.8, the acceleration due to gravity. In this version, we call acceleration to compute the total acceleration due to gravity and drag .

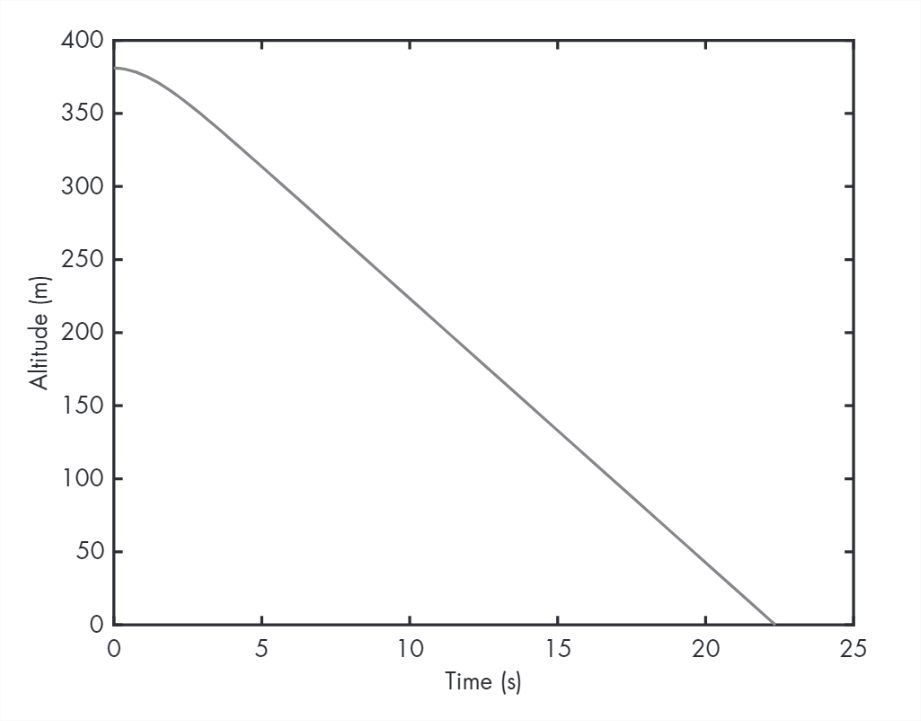
11.2.jpg — Figure 11.2: Altitude versus time for a penny in free fall with air resistance

Everything else is the same. Figure 11.2 shows the result.

Air resistance makes a big difference! Velocity increases until acceleration due to drag equals acceleration due to gravity; after that, velocity is constant and position decreases linearly (and much more slowly than it would in a vacuum).

With air resistance, the time until the penny hits the sidewalk is 22.4 s, substantially longer than before (8.8 s).

And the final velocity is 18.1 m/s, substantially slower than before (86 m/s).