4.4: Interpreting results
- Page ID
- 12746
Based on our understanding of how ArrayList works, we expect the add method to take constant time when we add elements to the end. So the total time to add n elements should be linear.
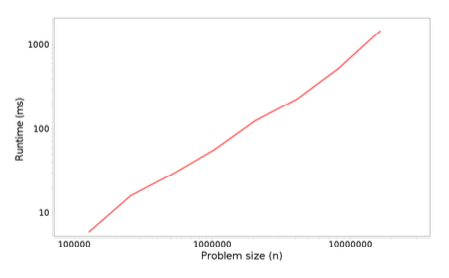
Figure \(\PageIndex{1}\): Profiling results: run time versus problem size for adding n elements to the end of an ArrayList.
To test that theory, we could plot total run time versus problem size, and we should see a straight line, at least for problem sizes that are big enough to measure accurately. Mathematically, we can write the function for that line:
\[ runtime = a + bn \nonumber \]
where a is the intercept of the line and b is the slope.
On the other hand, if add is linear, the total time for n adds would be quadratic. If we plot run time versus problem size, we expect to see a parabola. Or mathematically, something like:
\[ runtime = a + bn + cn^2 \nonumber \]
With perfect data, we might be able to tell the difference between a straight line and a parabola, but if the measurements are noisy, it can be hard to tell. A better way to interpret noisy measurements is to plot run time and problem size on a log-log scale.
Why? Let’s suppose that run time is proportional to \( n^k \), but we don’t know what the exponent k is. We can write the relationship like this:
\[ runtime - a + bn + \dots + cn^k \nonumber \]
For large values of n, the term with the largest exponent is the most important, so:
\[ runtime \approx cn^k \nonumber \]
where \( \approx \) means “approximately equal”. Now, if we take the logarithm of both sides of this equation:
\[ \log(runtime) \approx \log(c) + k\log(n) \nonumber \]
This equation implies that if we plot runtime versus n on a log-log scale, we expect to see a straight line with intercept \( \log(c) \) and slope k. We don’t care much about the intercept, but the slope indicates the order of growth: if \( k = 1\), the algorithm is linear; if \( k = 2 \), it’s quadratic.
Looking at the figure in the previous section, you can estimate the slope by eye. But when you call plotResults it computes a least squares fit to the data and prints the estimated slope. In this example:
Estimated slope = 1.06194352346708
which is close to 1; and that suggests that the total time for n adds is linear, so each add is constant time, as expected.
One important point: if you see a straight line on a graph like this, that does not mean that the algorithm is linear. If the run time is proportional to \( n^k \) for any exponent k, we expect to see a straight line with slope k. If the slope is close to 1, that suggests the algorithm is linear. If it is close to 2, it’s probably quadratic.


