6.5: Binary Search Trees
- Page ID
- 46729
A typical binary search tree looks like this:
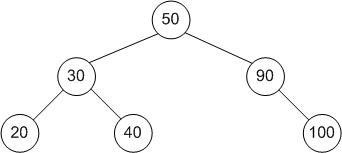
Terms
Node: Any item that is stored in the tree.
Root: The top item in the tree. (50 in the tree above)
Child: Node(s) under the current node. (20 and 40 are children of 30 in the tree above)
Parent: The node directly above the current node. (90 is the parent of 100 in the tree above)
Leaf: A node which has no children. (20 is a leaf in the tree above)
Searching through a binary search tree
To search for an item in a binary tree:
- Start at the root node
- If the item that you are searching for is less than the root node, move to the left child of the root node, if the item that you are searching for is more than the root node, move to the right child of the root node and if it is equal to the root node, then you have found the item that you are looking for.
- Now check to see if the item that you are searching for is equal to, less than or more than the new node that you are on. Again if the item that you are searching for is less than the current node, move to the left child, and if the item that you are searching for is greater than the current node, move to the right child.
- Repeat this process until you find the item that you are looking for or until the node does not have a child on the correct branch, in which case the tree doesn't contain the item which you are looking for.
Example

For example, to find the node 40...
- The root node is 50, which is greater than 40, so you go to 50's left child.
- 50's left child is 30, which is less than 40, so you next go to 30's right child.
- 30's right child is 40, so you have found the item that you are looking for :)
.........
Adding an item to a binary search tree
- To add an item, you first must search through the tree to find the position that you should put it in. You do this following the steps above.
- When you reach a node which doesn't contain a child on the correct branch, add the new node there.
For example, to add the node 25...
- The root node is 50, which is greater than 25, so you go to 50's left child.
- 50's left child is 30, which is greater than 25, so you go to 30's left child.
- 30's left child is 20, which is less than 25, so you go to 20's right child.
- 20's right child doesn't exist, so you add 25 there :)
Deleting an item from a binary search tree
It is assumed that you have already found the node that you want to delete, using the search technique described above.
Case 1: The node you want to delete is a leaf
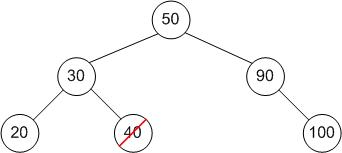
For example, to delete 40...
- Simply delete the node!
Case 2: The node you want to delete has one child
- Directly connect the child of the node that you want to delete, to the parent of the node that you want to delete.

For example, to delete 90...
- Delete 90, then make 100 the child node of 50.
Case 3: The node you want to delete has two children
One non-standard way, is to rotate the node into a chosen subtree, and attempt to delete the key again from that subtree, recursively, until Case 1 or Case 2 occurs. This could unbalance a tree, so randomly choosing whether to right or left rotate may help.
The standard way is to pick either the left or right child, say the right, then get the right's leftmost descendent by following left ,starting from the right child, until the next left is null. Then remove this leftmost descendant of the right child, replacing it with its right sub-tree (it has a left child of null). Then use the contents of this former leftmost descendant of the right child, as replacement for the key and value of the node being deleted , so that its values now are in the deleted node, the parent of the right child. This still maintains the key ordering for all nodes. Example java code is below in the treap example code.
The following examples use the standard algorithm, that is, the successor is the left-most node in the right subtree of the node to be deleted.
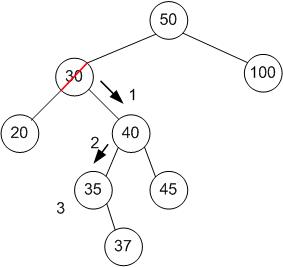
For example, to delete 30
- The right node of the node which is being deleted is 40.
- (From now on, we continually go to the left node until there isn't another one...) The first left node of 40, is 35.
- 35 has no left node, therefore 35 is the successor!
- 35 replaces 30, at the original right node, and the node with 35 is deleted, replacing it with the right sub-tree, which has the root node 37.
Case 1 of two-children case: The successor is the right child of the node being deleted
- Directly move the child to the right of the node being deleted into the position of the node being deleted.
- As the new node has no left children, you can connect the deleted node's left subtree's root as it's left child.
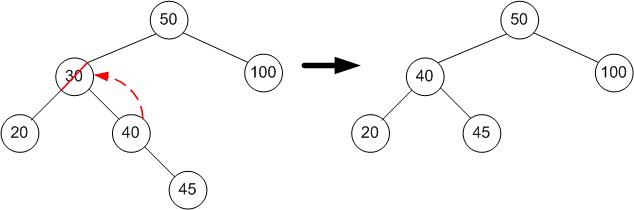
For example, to delete 30
- replace the contents to be deleted (30), with the successor's contents (40).
- delete the successor node (contents 40), replacing it with its right subtree (head contents 45).
Case 2 of two-children case: The successor isn't the right child of the node being deleted
This is best shown with an example

To delete 30...
- Replace the contents to be deleted (30) with the successor's contents (35).
- replace the successor (35) with its right subtree (37). There is no left subtree because the successor is leftmost.


