1.3: Mathematical Background
- Page ID
- 8430
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we review some mathematical notations and tools used throughout this book, including logarithms, big-Oh notation, and probability theory. This review will be brief and is not intended as an introduction. Readers who feel they are missing this background are encouraged to read, and do exercises from, the appropriate sections of the very good (and free) textbook on mathematics for computer science [50].
\(\PageIndex{1}\) Exponentials and Logarithms
The expression \(b^x\) denotes the number \(b\) raised to the power of \(x\). If \(x\) is a positive integer, then this is just the value of \(b\) multiplied by itself \(x-1\) times:
\[b^x = \underbrace{b\times b\times \cdots \times b}_{x} \enspace .\nonumber\]
When \(x\) is a negative integer, \(b^x=1/b^{-x}\). When \(x=0\), \(b^x=1\). When \(b\) is not an integer, we can still define exponentiation in terms of the exponential function \(e^x\) (see below), which is itself defined in terms of the exponential series, but this is best left to a calculus text.
In this book, the expression \(\log_b k\) denotes the base-\(b\) logarithm of \(k\). That is, the unique value \(x\) that satisfies
\[b^{x} = k \enspace .\nonumber\]
Most of the logarithms in this book are base 2 (binary logarithms). For these, we omit the base, so that \(\log k\) is shorthand for \(\log_2 k\).
An informal, but useful, way to think about logarithms is to think of \(\log_b k\) as the number of times we have to divide \(k\) by \(b\) before the result is less than or equal to 1. For example, when one does binary search, each comparison reduces the number of possible answers by a factor of 2. This is repeated until there is at most one possible answer. Therefore, the number of comparison done by binary search when there are initially at most \(n+1\) possible answers is at most \(\lceil\log_2(n+1)\rceil\).
Another logarithm that comes up several times in this book is the natural logarithm. Here we use the notation \(\ln k\) to denote \(\log_e k\), where \(e\) -- Euler's constant -- is given by
\[e = \lim_{n\rightarrow\infty} \left(1+\frac{1}{n}\right)^n \approx 2.71828 \enspace .\nonumber\]
The natural logarithm comes up frequently because it is the value of a particularly common integral:
\[\int_{1}^{k} 1/x\,\mathrm{d}x = \ln k \enspace .\nonumber\]
Two of the most common manipulations we do with logarithms are removing them from an exponent:
\[b^{\log_b k} = k\nonumber\]
and changing the base of a logarithm:
\[\log_b k = \frac{\log_a k}{\log_a b} \enspace .\nonumber\]
For example, we can use these two manipulations to compare the natural and binary logarithms
\[\ln k = \frac{\log k}{\log e} = \frac{\log k}{(\ln e)/(\ln 2)} = (\ln 2)(\log k) \approx 0.693147\log k \enspace .\nonumber\]
\(\PageIndex{2}\) Factorials
In one or two places in this book, the factorial function is used. For a non-negative integer \(n\), the notation \(n!\) (pronounced "\(n\) factorial") is defined to mean
\[ n! = 1\cdot2\cdot3\cdot\cdots\cdot n \enspace . \nonumber\]
Factorials appear because \(n!\) counts the number of distinct permutations, i.e., orderings, of \(n\) distinct elements. For the special case \(n=0\), \(0!\) is defined as 1.
The quantity \(n!\) can be approximated using Stirling's Approximation:
\[ n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^{n}e^{\alpha(n)} \enspace , \nonumber\]
where
\[ \frac{1}{12n+1} < \alpha(n) < \frac{1}{12n} \enspace . \nonumber\]
Stirling's Approximation also approximates \(\ln(n!)\):
\[ \ln(n!) = n\ln n - n + \frac{1}{2}\ln(2\pi n) + \alpha(n) \nonumber\]
(In fact, Stirling's Approximation is most easily proven by approximating \(\ln(n!)=\ln 1 + \ln 2 + \cdots + \ln n\) by the integral \(\int_1^n \ln n\,\mathrm{d}n = n\ln n - n +1\).)
Related to the factorial function are the binomial coefficients. For a non-negative integer \(n\) and an integer \(k\in\{0,\ldots,n\}\), the notation \(\binom{n}{k}\) denotes:
\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \enspace . \nonumber\]
The binomial coefficient \(\binom{n}{k}\) (pronounced "\(n\) choose \(k\)") counts the number of subsets of an \(n\) element set that have size \(k\), i.e., the number of ways of choosing \(k\) distinct integers from the set \(\{1,\ldots,n\}\).
\(\PageIndex{3}\) Asymptotic Notation
When analyzing data structures in this book, we want to talk about the running times of various operations. The exact running times will, of course, vary from computer to computer and even from run to run on an individual computer. When we talk about the running time of an operation we are referring to the number of computer instructions performed during the operation. Even for simple code, this quantity can be difficult to compute exactly. Therefore, instead of analyzing running times exactly, we will use the so-called big-Oh notation: For a function \(f(n)\), \(O(f(n))\) denotes a set of functions,
\[ O(f(n)) = \left\{ \begin{array}{l} g(n):\mbox{there exists $c>0$, and $n_0$ such that}\\ \quad\mbox{$g(n) \le c\cdot f(n)$ for all $n\ge n_0$} \end{array} \right\} \enspace . \nonumber\]
Thinking graphically, this set consists of the functions \(g(n)\) where \(c\cdot f(n)\) starts to dominate \(g(n)\) when \(n\) is sufficiently large.
We generally use asymptotic notation to simplify functions. For example, in place of \(5n\log n + 8n - 200\) we can write \(O(n\log n)\). This is proven as follows:
\[\begin{align}
5n\log n + 8n - 200 &\le 5n\log n + 8n\nonumber\\
&\le 5n\log n + 8n\log n
\qquad \mbox{ for $n\ge 2$ (so that $\log n \ge 1$)}\nonumber\\
&\le 13n\log n \enspace .\nonumber
\end{align}\nonumber\]
This demonstrates that the function \(f(n)=5n\log n + 8n - 200\) is in the set \(O(n\log n)\) using the constants \(c=13\) and \(n_0 = 2\).
A number of useful shortcuts can be applied when using asymptotic notation. First:
\[ O(n^{c_1}) \subset O(n^{c_2}) \enspace ,\nonumber\]
for any \(c_1 < c_2\). Second: For any constants \(a,b,c > 0\),
\[ O(a) \subset O(\log n) \subset O(n^{b}) \subset O({c}^n) \enspace . \nonumber\]
These inclusion relations can be multiplied by any positive value, and they still hold. For example, multiplying by \(n\) yields:
\[ O(n) \subset O(n\log n) \subset O(n^{1+b}) \subset O(n{c}^n) \enspace . \nonumber\]
Continuing in a long and distinguished tradition, we will abuse this notation by writing things like \(f_1(n) = O(f(n))\) when what we really mean is \(f_1(n) \in O(f(n))\). We will also make statements like "the running time of this operation is \(O(f(n))\)" when this statement should be "the running time of this operation is a member of \(O(f(n))\)." These shortcuts are mainly to avoid awkward language and to make it easier to use asymptotic notation within strings of equations.
A particularly strange example of this occurs when we write statements like
\[ T(n) = 2\log n + O(1) \enspace . \nonumber\]
Again, this would be more correctly written as
\[ T(n) \le 2\log n + [
\mbox{some member of $O(1)$]}
\enspace .
\nonumber\]
The expression \(O(1)\) also brings up another issue. Since there is no variable in this expression, it may not be clear which variable is getting arbitrarily large. Without context, there is no way to tell. In the example above, since the only variable in the rest of the equation is \(n\), we can assume that this should be read as \(T(n) = 2\log n + O(f(n))\), where \(f(n) = 1\).
Big-Oh notation is not new or unique to computer science. It was used by the number theorist Paul Bachmann as early as 1894, and is immensely useful for describing the running times of computer algorithms. Consider the following piece of code:
void snippet() {
for (int i = 0; i < n; i++)
a[i] = i;
}
One execution of this method involves
- \(1\) assignment ( \(\mathtt{int\, i\, =\, 0}\)),
- \(\mathtt{n}+1\) comparisons ( \(\mathtt{i < n}\)),
- \(\mathtt{n}\) increments ( \(\mathtt{i++}\)),
- \(\mathtt{n}\) array offset calculations ( \(\mathtt{a[i]}\)), and
- \(\mathtt{n}\) indirect assignments ( \(\mathtt{a[i] = i}\)).
So we could write this running time as
\[ T(\mathtt{n})=a + b(\mathtt{n}+1) + c\mathtt{n} + d\mathtt{n} + e\mathtt{n} \enspace , \nonumber\]
where \(a\), \(b\), \(c\), \(d\), and \(e\) are constants that depend on the machine running the code and represent the time to perform assignments, comparisons, increment operations, array offset calculations, and indirect assignments, respectively. However, if this expression represents the running time of two lines of code, then clearly this kind of analysis will not be tractable to complicated code or algorithms. Using big-Oh notation, the running time can be simplified to
\[ T(\mathtt{n})= O(\mathtt{n}) \enspace . \nonumber\]
Not only is this more compact, but it also gives nearly as much information. The fact that the running time depends on the constants \(a\), \(b\), \(c\), \(d\), and \(e\) in the above example means that, in general, it will not be possible to compare two running times to know which is faster without knowing the values of these constants. Even if we make the effort to determine these constants (say, through timing tests), then our conclusion will only be valid for the machine we run our tests on.
Big-Oh notation allows us to reason at a much higher level, making it possible to analyze more complicated functions. If two algorithms have the same big-Oh running time, then we won't know which is faster, and there may not be a clear winner. One may be faster on one machine, and the other may be faster on a different machine. However, if the two algorithms have demonstrably different big-Oh running times, then we can be certain that the one with the smaller running time will be faster for large enough values of \(\mathtt{n}\).
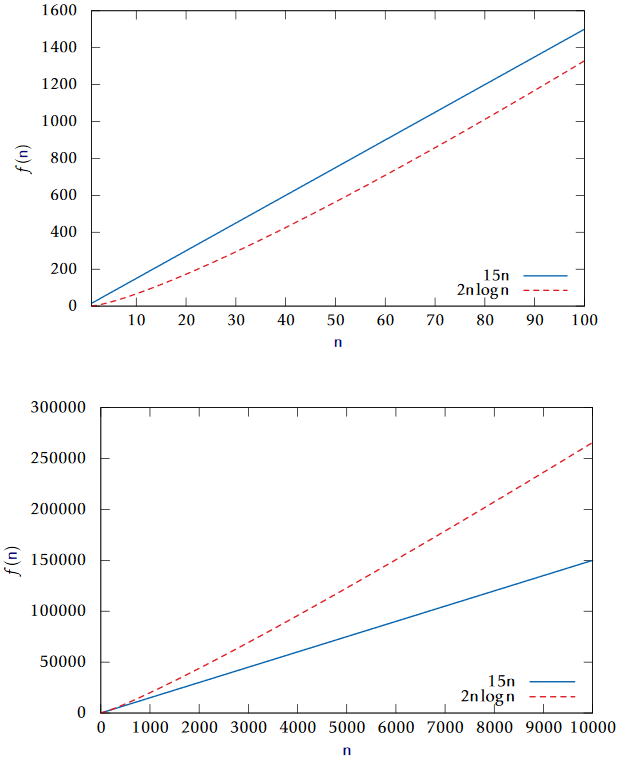
An example of how big-Oh notation allows us to compare two different functions is shown in Figure \(\PageIndex{1}\), which compares the rate of growth of \(f_1(\mathtt{n})=15\mathtt{n}\) versus \(f_2(n)=2\mathtt{n}\log\mathtt{n}\). It might be that \(f_1(n)\) is the running time of a complicated linear time algorithm while \(f_2(n)\) is the running time of a considerably simpler algorithm based on the divide-and-conquer paradigm. This illustrates that, although \(f_1(\mathtt{n})\) is greater than \(f_2(n)\) for small values of \(\mathtt{n}\), the opposite is true for large values of \(\mathtt{n}\). Eventually \(f_1(\mathtt{n})\) wins out, by an increasingly wide margin. Analysis using big-Oh notation told us that this would happen, since \(O(\mathtt{n})\subset O(\mathtt{n}\log \mathtt{n})\).
In a few cases, we will use asymptotic notation on functions with more than one variable. There seems to be no standard for this, but for our purposes, the following definition is sufficient:
\[ O(f(n_1,\ldots,n_k))
= \left\{
\begin{array}{@{}l@{}}
g(n_1,\ldots,n_k):\mbox{there exists $c>0$, and $z$ such that} \\
\quad g(n_1,\ldots,n_k)\le c\cdot f (n_1,\ldots,n_k)\\
\qquad\mbox{for all $n_1,\ldots,n_k$ such that $g(n_1,\ldots,n_k)\ge z$}
\end{array}
\right\} \enspace . \nonumber\]
This definition captures the situation we really care about: when the arguments \(n_1,\ldots,n_k\) make \(g\) take on large values. This definition also agrees with the univariate definition of \(O(f(n))\) when \(f(n)\) is an increasing function of \(n\). The reader should be warned that, although this works for our purposes, other texts may treat multivariate functions and asymptotic notation differently.
\(\PageIndex{4}\) Randomization and Probability
Some of the data structures presented in this book are randomized; they make random choices that are independent of the data being stored in them or the operations being performed on them. For this reason, performing the same set of operations more than once using these structures could result in different running times. When analyzing these data structures we are interested in their average or expected running times.
Formally, the running time of an operation on a randomized data structure is a random variable, and we want to study its expected value. For a discrete random variable \(X\) taking on values in some countable universe \(U\), the expected value of \(X\), denoted by \(\mathrm{E}[X]\), is given by the formula
\[ \mathrm{E}[X] = \sum_{x\in U} x\cdot\Pr\{X=x\} \enspace . \nonumber\]
Here \(\Pr\{\mathcal{E}\}\) denotes the probability that the event \(\mathcal{E}\) occurs. In all of the examples in this book, these probabilities are only with respect to the random choices made by the randomized data structure; there is no assumption that the data stored in the structure, nor the sequence of operations performed on the data structure, is random.
One of the most important properties of expected values is linearity of expectation. For any two random variables \(X\) and \(Y\),
\[ \mathrm{E}[X+Y] = \mathrm{E}[X] + \mathrm{E}[Y] \enspace . \nonumber\]
More generally, for any random variables \(X_1,\ldots,X_k\),
\[ \mathrm{E}\left[\sum_{i=1}^k X_k\right] = \sum_{i=1}^k \mathrm{E}[X_i] \enspace . \nonumber\]
Linearity of expectation allows us to break down complicated random variables (like the left hand sides of the above equations) into sums of simpler random variables (the right hand sides).
A useful trick, that we will use repeatedly, is defining indicator random variables. These binary variables are useful when we want to count something and are best illustrated by an example. Suppose we toss a fair coin \(k\) times and we want to know the expected number of times the coin turns up as heads. Intuitively, we know the answer is \(k/2\), but if we try to prove it using the definition of expected value, we get
\[\begin{align}
\mathrm{E}[X]
&= \sum_{i=0}^k i\cdot\Pr\{X=i\}\nonumber\\
&= \sum_{i=0}^k i\cdot\binom{k}{i}/2^k\nonumber\\
&= k\cdot \sum_{i=0}^{k-1}\binom{k-1}{i}/2^k\nonumber\\
&= k/2 \enspace .\nonumber
\end{align}\nonumber\]
This requires that we know enough to calculate that \(\Pr\{X=i\} = \binom{k}{i}/2^k\), and that we know the binomial identities \(i\binom{k}{i}=k\binom{k-1}{i}\) and \(\sum_{i=0}^{k} \binom{k}{i} = 2^{k}\).
Using indicator variables and linearity of expectation makes things much easier. For each \(i\in\{1,\ldots,k\}\), define the indicator random variable
\[ I_i = \begin{cases} 1 & \text{if the $i$th coin toss is heads} \\ 0 & \text{otherwise.} \end{cases}\nonumber\]
Then
\[ \mathrm{E}[I_i] = (1/2)1 + (1/2)0 = 1/2 \enspace . \nonumber\]
Now, \(X=\sum_{i=1}^k I_i\), so
\[\begin{align}
\mathrm{E}[X]
&= \mathrm{E}\left[\sum_{i=1}^k I_i\right] \nonumber\\
&= \sum_{i=1}^k \mathrm{E}[I_i]\nonumber\\
&= \sum_{i=1}^k 1/2 \nonumber\\
&= k/2 \enspace .\nonumber
\end{align}\nonumber\]
This is a bit more long-winded, but doesn't require that we know any magical identities or compute any non-trivial probabilities. Even better, it agrees with the intuition that we expect half the coins to turn up as heads precisely because each individual coin turns up as heads with a probability of \(1/2\).


