12.1: Representing a Graph by a Matrix
- Page ID
- 8485
An adjacency matrix is a way of representing an \(\mathtt{n}\) vertex graph \(G=(V,E)\) by an \(\mathtt{n}\times\mathtt{n}\) matrix, \(\mathtt{a}\), whose entries are boolean values.
int n;
boolean[][] a;
AdjacencyMatrix(int n0) {
n = n0;
a = new boolean[n][n];
}
The matrix entry \(\mathtt{a[i][j]}\) is defined as
\[\mathtt{a[i][j]}=
\begin{cases}
\mathtt{true} & \text{if } \mathtt{(i,j)}\in E \\
\mathtt{false} & \text{otherwise}
\end{cases}\nonumber\]
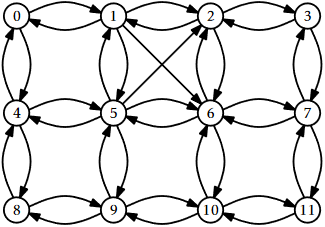
The adjacency matrix for the graph in Figure 12.1 is shown in Figure \(\PageIndex{1}\).
In this representation, the operations \(\mathtt{addEdge(i,j)}\), \(\mathtt{removeEdge(i,j)}\), and \(\mathtt{hasEdge(i,j)}\) just involve setting or reading the matrix entry \(\mathtt{a[i][j]}\):
void addEdge(int i, int j) {
a[i][j] = true;
}
void removeEdge(int i, int j) {
a[i][j] = false;
}
boolean hasEdge(int i, int j) {
return a[i][j];
}
These operations clearly take constant time per operation.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 7 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
Where the adjacency matrix performs poorly is with the \(\mathtt{outEdges(i)}\) and \(\mathtt{inEdges(i)}\) operations. To implement these, we must scan all \(\mathtt{n}\) entries in the corresponding row or column of \(\mathtt{a}\) and gather up all the indices, \(\mathtt{j}\), where \(\mathtt{a[i][j]}\), respectively \(\mathtt{a[j][i]}\), is true.
List<Integer> outEdges(int i) {
List<Integer> edges = new ArrayList<Integer>();
for (int j = 0; j < n; j++)
if (a[i][j]) edges.add(j);
return edges;
}
List<Integer> inEdges(int i) {
List<Integer> edges = new ArrayList<Integer>();
for (int j = 0; j < n; j++)
if (a[j][i]) edges.add(j);
return edges;
}
These operations clearly take \(O(\mathtt{n})\) time per operation.
Another drawback of the adjacency matrix representation is that it is large. It stores an \(\mathtt{n}\times \mathtt{n}\) boolean matrix, so it requires at least \(\mathtt{n}^2\) bits of memory. The implementation here uses a matrix of \(\mathtt{boolean}\) values so it actually uses on the order of \(\mathtt{n}^2\) bytes of memory. A more careful implementation, which packs \(\mathtt{w}\) boolean values into each word of memory, could reduce this space usage to \(O(\mathtt{n}^2/\mathtt{w})\) words of memory.
Theorem \(\PageIndex{1}\)
The AdjacencyMatrix data structure implements the Graph interface. An AdjacencyMatrix supports the operations
- \(\mathtt{addEdge(i,j)}\), \(\mathtt{removeEdge(i,j)}\), and \(\mathtt{hasEdge(i,j)}\) in constant time per operation; and
- \(\mathtt{inEdges(i)}\), and \(\mathtt{outEdges(i)}\) in \(O(\mathtt{n})\) time per operation.
The space used by an AdjacencyMatrix is \(O(\mathtt{n}^2)\).
Despite its high memory requirements and poor performance of the \(\mathtt{inEdges(i)}\) and \(\mathtt{outEdges(i)}\) operations, an AdjacencyMatrix can still be useful for some applications. In particular, when the graph \(G\) is dense, i.e., it has close to \(\mathtt{n}^2\) edges, then a memory usage of \(\mathtt{n}^2\) may be acceptable.
The AdjacencyMatrix data structure is also commonly used because algebraic operations on the matrix \(\mathtt{a}\) can be used to efficiently compute properties of the graph \(G\). This is a topic for a course on algorithms, but we point out one such property here: If we treat the entries of \(\mathtt{a}\) as integers (1 for \(\mathtt{true}\) and 0 for \(\mathtt{false}\)) and multiply \(\mathtt{a}\) by itself using matrix multiplication then we get the matrix \(\mathtt{a}^2\). Recall, from the definition of matrix multiplication, that
\[\mathtt{a^2[i][j]} = \sum_{k=0}^{\mathtt{n}-1} \mathtt{a[i][k]}\cdot \mathtt{a[k][j]} \enspace .\nonumber\]
Interpreting this sum in terms of the graph \(G\), this formula counts the number of vertices, \(\mathtt{k}\), such that \(G\) contains both edges \(\mathtt{(i,k)}\) and \(\mathtt{(k,j)}\). That is, it counts the number of paths from \(\mathtt{i}\) to \(\mathtt{j}\) (through intermediate vertices, \(\mathtt{k}\)) whose length is exactly two. This observation is the foundation of an algorithm that computes the shortest paths between all pairs of vertices in \(G\) using only \(O(\log \mathtt{n})\) matrix multiplications.