10.2: Functional Dependencies

To understand normalization theory (first, second, third and Boyce-Codd normal forms), we must understand what is meant by the term functional dependency. There is another type of dependency called a multi-valued dependency but that is important to the understanding of higher normal forms not covered in this text.

A functional dependency is an association between two attributes. We say there is a functional dependency from attribute A to an attribute B if and only if for each value of A there can be at most one value for B. We can illustrate this by writing

• A functionally determines B, or
• B is functionally determined by A, or
• by a drawing such as: A \(\rightarrow \) B

When we have a functional dependency from A to B we refer to attribute A as the determinant.

Example \(\PageIndex{1}\)

Consider a company collects information about each employee such as the employee’s identification number (ID), their first name, last name, salary and gender. As is typical, each employee is given a unique ID which serves to identify the employee. Hence for each value of ID there is at most one value for first name, last name, salary and gender. Therefore we have four functional dependencies where ID is the determinant; we can show this as a list or graphically:

Figure \(\PageIndex{1}\): Example #1 functional dependencies.

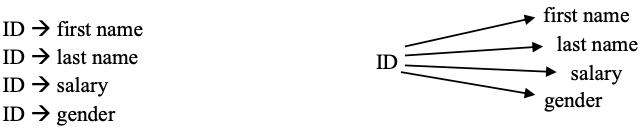
If you think about this case there cannot be any other FDs. For example, consider the gender attribute – we need to allow for more than one employee for a given gender, and so we cannot have a situation where gender functionally determines ID. So, gender \(\rightarrow \) ID cannot exist. Now consider the first name attribute. Again we need to allow for more than one employee to have the same first name and so first name cannot determine anything. Similarly for other attributes.

Example \(\PageIndex{2}\)

Recall the Department and Course tables introduced in Chapter 2 - sample data is shown below:

Table \(\PageIndex{1}\): Department table.

Department
deptCode	deptName	deptLocn	deptPhone	chairName
MATH	Mathematics	2R33	786-0033	Peter Smith
HIST	History	3D07	786-0300	Simon Lee
IS	Indigenous Studies	3C11	786-3322	Leslie Roman
MENN	Mennonite Studies	3C11	786-3322	Leslie Roman
BIOL	Biology	2L88	786-9843	James Dunn

Table \(\PageIndex{2}\): Course table.

Course
deptCode	courseNo	title	description	creditHours
HIST	1010	Introduction to History	Within a relatively small lecture/seminar setting, this course introduces you to the ways in which people try to understand their present by studying their past.	6
IS	1010	Indigenous Ways of Knowing	This course offers an introduction to Indigenous ways of knowing through active participation in strategies that facilitate the production of Aboriginal knowledge and through comparisons with Euro-American ways of knowing.	3
MENN	1010	Mennonites and the Modern World	This course is a history of the ethnic identity and religious faith of the Mennonites from the sixteenth century to the present.	6
IS	1201	Introductory Ojibwe	This course is intended for students who are not fluent in Ojibwe and have never taken a course in the language	6
BIOL	2401	Forest Field Skills Camp	This intensive two-week field course is mandatory for students in the Forest Ecology program and is designed to give students field survival and basic forestry skills.	1

Recall the primary keys (underlined above) of these two tables:

Table \(\PageIndex{3}\): Primary keys.

Table	PK
Department	deptCode
Course	deptCode, courseNo

Consider the Department table where deptCode is the primary key. For each value of deptCode there is at most one value for deptName, deptLocn, deptPhone, and chairName. You should agree the following FDs exist:

deptCode \(\rightarrow \) deptName

deptCode \(\rightarrow \) deptLocn

deptCode \(\rightarrow \) deptPhone

deptCode \(\rightarrow \) chairName

Each row of the Course table has one value for title, one value for description, and one value for credit hours. The primary key of Course is consists of two attributes, deptCode and courseNo. The following FDs exist for the Course table:

deptCode, courseNo \(\rightarrow \) title

deptCode, courseNo \(\rightarrow \) description

deptCode, courseNo \(\rightarrow \) credit hours

In this case we have a determinant comprising two attributes; the determinant is composite. We can draw the functional dependencies as:

Figure \(\PageIndex{2}\): Example #2 functional dependencies.

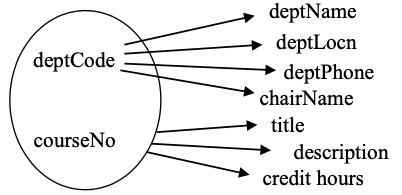
Could there be other functional dependencies in this situation?

These examples demonstrate that there is a FD from the primary key to each of the other attributes in a table.

Example \(\PageIndex{3}\)

The following ERD is shown in the Chen notation. There is one entity type named Employee that has 4 attributes. In this design there are two keys (id and sin) and two descriptive attributes (firstName and lastName):

Figure \(\PageIndex{3}\): Example #3 ERD.

Each symbol in an ERD contains information about a model. From the above we know there are two keys – id and sin. An id value, or a sin value, will uniquely identify an employee and so we have the six FDs:

Figure \(\PageIndex{4}\): Example #3 functional dependencies.

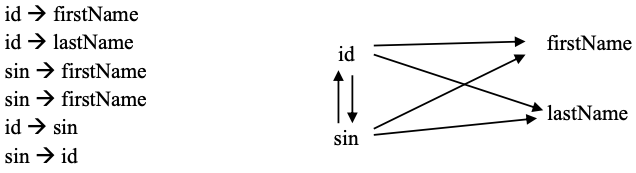
This example shows that an ERD carries information that can be expressed in terms of FDs.

Exercises (Set 1)

Exercise \(\PageIndex{1}\)

Consider the Product table below where productID is the PK. What FDs must exist in this table:

productID	description	unit price	quantity on hand
33	16 oz. can tomato soup	1.00	50
41	454 gram box corn flakes	4.50	39
45	Package red licorice	1.00	39
46	Package black licorice	1.00	50
47	1 litre 1% milk	1.99	25

Exercise \(\PageIndex{2}\)

Consider the ERD where the entity type Employee has one key attribute, id, and the entity type Position has one key attribute, title. As well the ERD shows a one-to- many relationship assigned to which can be expressed as:

An employee is assigned to at most one position.

A position can be assigned to many employees.

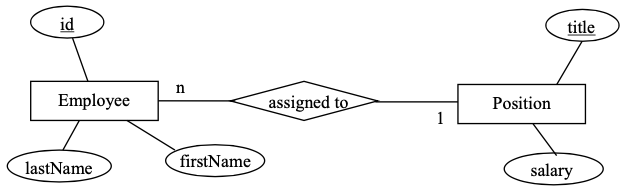
List the FDs that must be present.

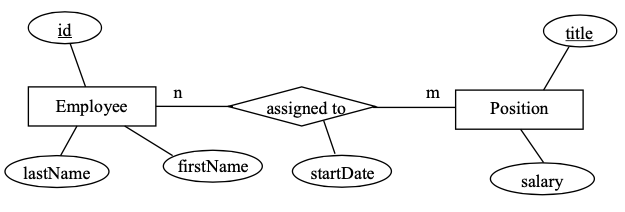
Exercise \(\PageIndex{3}\)

Consider this ERD that is similar to the above but where the assigned to relationship is many-to-many, and where assigned to has an attribute startDate. List the FDs that are present.

Exercise \(\PageIndex{4}\)

Consider the ERD below where Department has two keys deptCode and deptName – each department has a unique department code and has a unique department name. Course is a weak entity type with a partial key courseNo, and where offers is an identifying relationship.

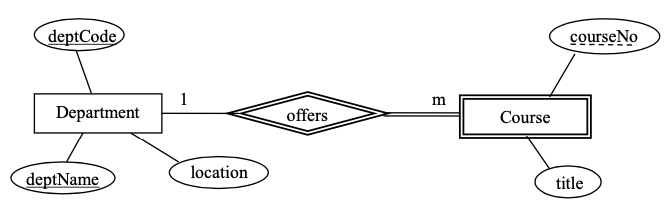
List the FDs that must exist.

Exercise \(\PageIndex{5}\)

Consider the table with attributes A, B and C.

A	B	C
1	33	100
2	33	200
3	22	200
1	33	101
2	33	350
4	67	350
5	67	101

Suppose there are many more rows that are not shown.

1. Is there a functional dependency from B to A? Explain your answer.
2. The rows that are shown suggest there could be a functional dependency A \(\rightarrow \) B. Compose a database query that would list rows, if they exist, that are counterexamples to the functional dependency A \(\rightarrow \) B. Such a query would list rows in the table where two or more rows have the same value for A but different values for B.

---

Keys and Non-Keys

Before going further, we need to be clear regarding the concept of key. We define the key of a relation to be any minimal set of attributes that uniquely identify tuples in the relation. We say minimal in order to eliminate trivial cases. Consider: if attribute k is a key and uniquely identifies a tuple then any combination of attributes that include k must also uniquely identify tuples. So, we restrict keys to be minimal sets of attributes that retain the property of unique identification. Further, we define candidate keys to be the collection of keys for a relation; a database designer must choose one of the candidate keys to be the primary key.

Additionally we define key attributes to be those attributes that are part of a key, and non-key attributes are those attributes that are not part of any key.

---

Anomalies

An anomaly is a variation that differs in some way from what is considered normal. With regards to maintaining a database, we consider the actions that must occur when data is updated, inserted, or deleted. In database applications where these update, insert, and/or delete operations are common (e.g. OLTP databases), it is desirable for these operations to be as simple and efficient as possible.

When relations are not fully normalized they exhibit update anomalies because basic operations are not as simple as possible. When relations are not fully normalized, some aspect of the relation will be awkward to maintain.

Consider the relation structure and sample data:

Table \(\PageIndex{4}\): Sample relation data.

deptNum	courseNum	studNum	grade	studName
92	101	3344	A	Joe
92	115	7654	A	Brenda
81	101	7654	C	Brenda
92	226	3344	B	Joe

This relation is used for keeping track of students enrollments, the grade assigned, and (oddly) the student’s name.

What must happen if a student’s name were to change? We should want our databases to have correct information, and so the name may need to be changed in several records, not just one. This is an example of an update anomaly – the simple change of a student’s name affects, not just one record, but potentially several in the database. The update operation is more complex than necessary, and this means it is more expensive to do, resulting in slower performance. When operations become more complex than necessary there is also a chance the operation is programmed incorrectly resulting in corrupted data – another unfortunate consequence.

Consider the Course and Department tables again, but now consider that they are combined into a single table. Obviously, this is a table with a considerable redundancy – for each course in the same department, the department location, phone, and chair must be repeated.

Table \(\PageIndex{5}\): Course and Department table headers.

Department_Course
deptCode	deptName	deptLocation	deptPhone	chairName	courseNo	title	description	creditHours

The primary key of such a table must be {deptCode, courseNo}. Consider for the following, however unlikely the situation seems, that the Deparment_Course table is the only table where department information is kept. Note that our point here is only to show, for a simple example, how redundancy leads to difficult semantics for database operations.

Insert anomaly

Suppose the university added a new department but there are no courses for that department yet. How can a row be added to the above table? Recall that no part of a primary key can be null, and so we can’t insert a row for a new department because we do not have a value for courseNo. This is an example of an insertion anomaly.

Delete anomaly

Suppose some department is undergoing a major reorganization. All courses are to be removed and later on some new courses will be added. If we delete all courses then we lose all the information in the database for that department.

The previous discussion concerning anomalies highlights some of the data management issues that arise when a relation is not fully normalized. Another way of describing the general problem here, as far as updating a database is concerned, is that redundant data makes it more complicated for us to keep the data consistent.

---

Partial Functional Dependencies

Consider a relation with department number, department chair name, course number and course title attributes. The combination {department number, course number} must be a key. The directed lines depict the FDs that are present.

Figure \(\PageIndex{5}\): Relation diagram with FDs.

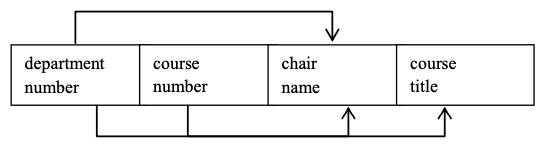
Note the functional dependency of chair name on department number. If two or more rows in the relation have the same value for department number, they must have the same value for chair name. We say this redundancy is due to the FD of chair name on department number. Because chair name is a non-key attribute and is dependent on department number, a subset of a key, we call this dependency a partial dependency.

In general, if we have a composite key {A, B} and the dependencies below

Figure \(\PageIndex{6}\): General relation diagram with FDs.

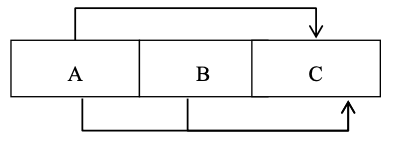
we say that C is partially dependent on {A, B}.

Exercises (Set 2)

Exercise \(\PageIndex{6}\)

Suppose each delivery of a course is called a section. In any one term suppose a course may have multiple sections and each section is assigned an instructor. Each course has a course title. Consider a Section relation where the PK is {dept number, course number, section number}. What FDs exist? Is there a partial dependency?

deptNo	courseNo	sectionNo	instructor	title
91	1906	001	J. Smith	Java I
91	1906	002	D. Grand	Java I
91	1910	001	J. Smith	Java II
91	1910	002	J. Daniels	Java II
53	1906	001	S. Farrell	History of the World
...	...	...	...	...

Exercise \(\PageIndex{7}\)

Consider a relation with attributes X, Y, Z, W where the only CK is {X,Y}, and where the FDs are {X,Y} \(\rightarrow \) Z, {X,Y} \(\rightarrow \) W, and Y \(\rightarrow \) W. Is there a partial dependency?

---

Transitive Functional Dependencies

Consider a relation that describes a couple of concepts, say instructor and department, and where the building shown is the building where the department is located, and the attribute instructor number is the only key:

instructor number	instructor name	office	department code	building
33	Joe	3D15	B&A	Buhler
44	Joe	3D16	ACS	Duckworth
45	April	3D17	ACS	Duckworth
50	Susan	3D17	ACS	Duckworth
21	Peter	3D18	B&A	Buhler
22	Peter	3D18	MATH	Duckworth

As instructor number is the only key, we have the following FDs:

Figure \(\PageIndex{7}\): Instructor number FDs.

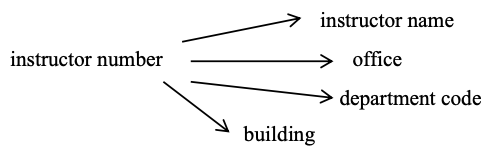
Suppose we also have the FD: department code determines building. Now our FD diagram becomes:

Figure \(\PageIndex{8}\): Instructor number FDs with building dependency.

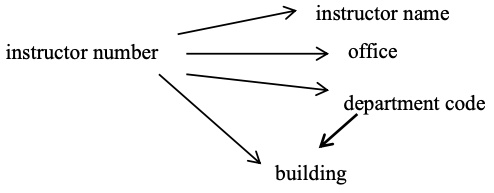
and we say the FD from instructor number to building is transitive via department code.

In general, if we have a relation with key A and functional dependencies: A \(\rightarrow \) B and B \(\rightarrow \) C, then we say attribute A transitively determines attribute C.

Figure \(\PageIndex{9}\): Non-key attributes and a transitive dependency.

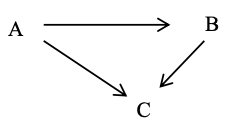
Note

B and C above are non-key attributes. If we also had the functional dependency BA (and so A and B are candidate keys) then A does not transitively determine C.

Exercises (Set 3)

Exercise \(\PageIndex{8}\)

Consider a relation that describes an employee including the province where the employee was born. Suppose the only key is employeeId and we have the attributes: name, birthDate, birthProvince, currentPopulation.

Employee
employeeId	name	birthDate	birthProvince	currentPopulation
123	Joe	Jan 1, 1990	MB	1,200,000
222	Jennifer	Jan 5, 1988	SK	1,450,000
345	Jimmy	Feb 5, 1987	MB	1,200,000
...	...	...	...	...

What FDs would exist? Is there a transitive dependency?

Exercise \(\PageIndex{9}\)

Consider a relation with attributes X, Y, Z, W where the only CK is X, and the FDs are X \(\rightarrow\) Y, X \(\rightarrow\) Z, X \(\rightarrow\) W and Y \(\rightarrow\) Z. Is there a transitive dependency?