2.5: Reliable Transmission

2.5 Reliable Transmission

2.5 Reliable Transmission

As we saw in the previous section, frames are sometimes corrupted while in transit, with an error code like CRC used to detect such errors. While some error codes are strong enough also to correct errors, in practice the overhead is typically too large to handle the range of bit and burst errors that can be introduced on a network link. Even when error-correcting codes are used (e.g., on wireless links) some errors will be too severe to be corrected. As a result, some corrupt frames must be discarded. A link-level protocol that wants to deliver frames reliably must somehow recover from these discarded (lost) frames.

It's worth noting that reliability is a function that may be provided at the link level, but many modern link technologies omit this function. Furthermore, reliable delivery is frequently provided at higher levels, including both transport and sometimes, the application layer. Exactly where it should be provided is a matter of some debate and depends on many factors. We describe the basics of reliable delivery here, since the principles are common across layers, but you should be aware that we're not just talking about a link-layer function.

Reliable delivery is usually accomplished using a combination of two fundamental mechanisms—acknowledgments and timeouts. An acknowledgment (ACK for short) is a small control frame that a protocol sends back to its peer saying that it has received an earlier frame. By control frame we mean a header without any data, although a protocol can piggyback an ACK on a data frame it just happens to be sending in the opposite direction. The receipt of an acknowledgment indicates to the sender of the original frame that its frame was successfully delivered. If the sender does not receive an acknowledgment after a reasonable amount of time, then it retransmits the original frame. This action of waiting a reasonable amount of time is called a timeout.

The general strategy of using acknowledgments and timeouts to implement reliable delivery is sometimes called automatic repeat request (abbreviated ARQ). This section describes three different ARQ algorithms using generic language; that is, we do not give detailed information about a particular protocol's header fields.

Stop-and-Wait

The simplest ARQ scheme is the stop-and-wait algorithm. The idea of stop-and-wait is straightforward: After transmitting one frame, the sender waits for an acknowledgment before transmitting the next frame. If the acknowledgment does not arrive after a certain period of time, the sender times out and retransmits the original frame.

Timeline showing four different scenarios for the stop-and-wait algorithm. (a) The ACK is received before the timer expires; (b) the original frame is lost; (c) the ACK is lost; (d) the timeout fires too soon.

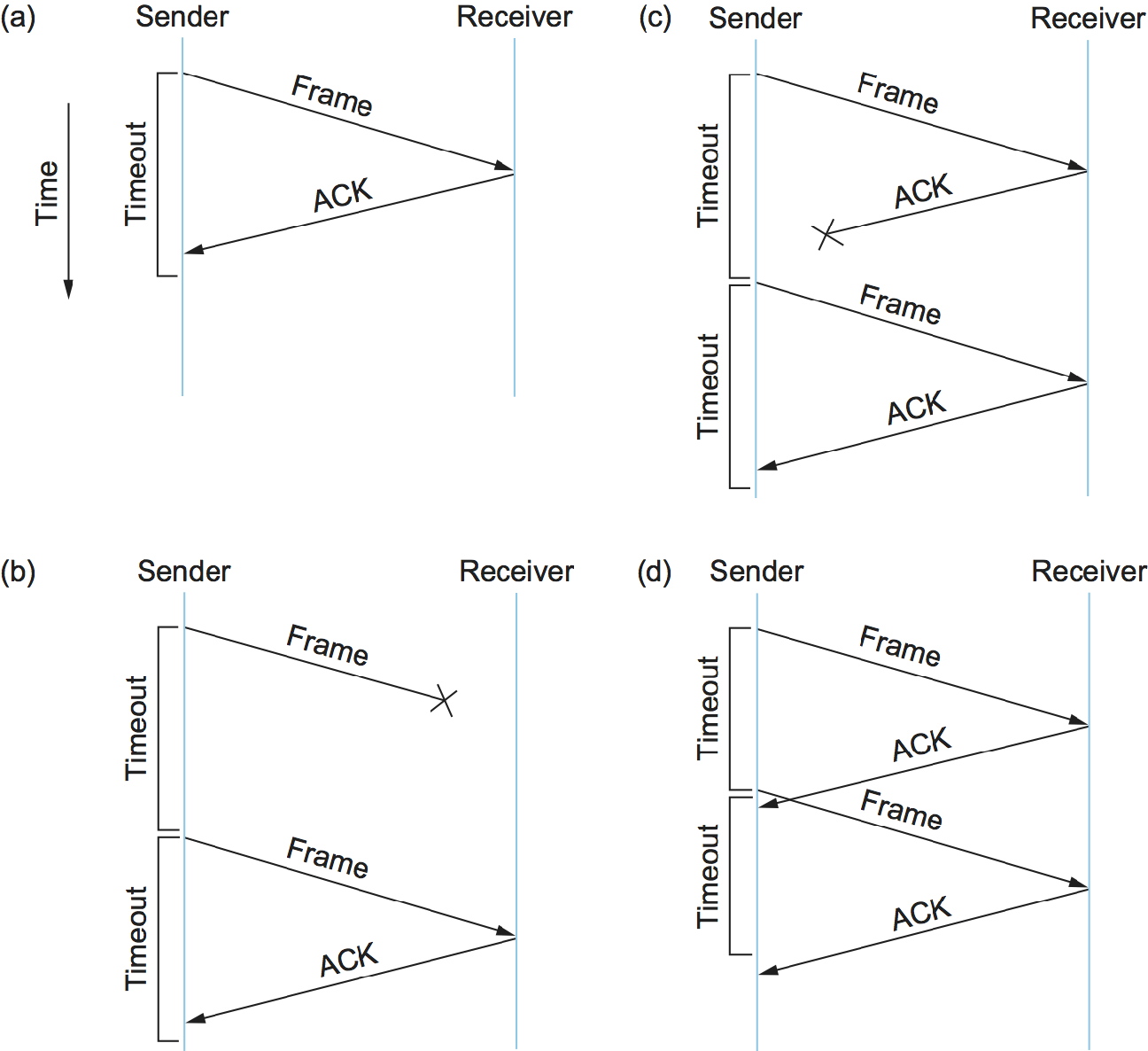
Figure 1 illustrates timelines for four different scenarios that result from this basic algorithm. The sending side is represented on the left, the receiving side is depicted on the right, and time flows from top to bottom. Figure 1(a) shows the situation in which the ACK is received before the timer expires; (b) and (c) show the situation in which the original frame and the ACK, respectively, are lost; and (d) shows the situation in which the timeout fires too soon. Recall that by "lost" we mean that the frame was corrupted while in transit, that this corruption was detected by an error code on the receiver, and that the frame was subsequently discarded.

The packet timelines shown in this section are examples of a frequently used tool in teaching, explaining, and designing protocols. They are useful because they capture visually the behavior over time of a distributed system—something that can be quite hard to analyze. When designing a protocol, you often have to be prepared for the unexpected—a system crashes, a message gets lost, or something that you expected to happen quickly turns out to take a long time. These sorts of diagrams can often help us understand what might go wrong in such cases and thus help a protocol designer be prepared for every eventuality.

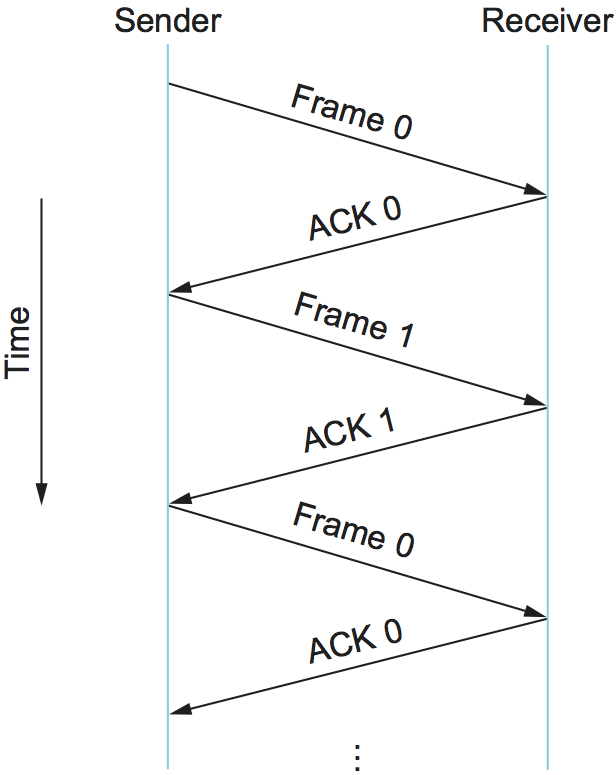
There is one important subtlety in the stop-and-wait algorithm. Suppose the sender sends a frame and the receiver acknowledges it, but the acknowledgment is either lost or delayed in arriving. This situation is illustrated in timelines (c) and (d) of Figure 1. In both cases, the sender times out and retransmits the original frame, but the receiver will think that it is the next frame, since it correctly received and acknowledged the first frame. This has the potential to cause duplicate copies of a frame to be delivered. To address this problem, the header for a stop-and-wait protocol usually includes a 1-bit sequence number—that is, the sequence number can take on the values 0 and 1—and the sequence numbers used for each frame alternate, as illustrated in Figure 2. Thus, when the sender retransmits frame 0, the receiver can determine that it is seeing a second copy of frame 0 rather than the first copy of frame 1 and therefore can ignore it (the receiver still acknowledges it, in case the first ACK was lost).

Timeline for stop-and-wait with 1-bit sequence number.

The main shortcoming of the stop-and-wait algorithm is that it allows the sender to have only one outstanding frame on the link at a time, and this may be far below the link's capacity. Consider, for example, a 1.5-Mbps link with a 45-ms round-trip time. This link has a delay $\times$ bandwidth product of 67.5 Kb, or approximately 8 KB. Since the sender can send only one frame per RTT, and assuming a frame size of 1 KB, this implies a maximum sending rate of

Bits-Per-Frame / Time-Per-Frame = 1024 x 8 / 0.045 = 182 kbps

or about one-eighth of the link's capacity. To use the link fully, then, we'd like the sender to be able to transmit up to eight frames before having to wait for an acknowledgment.

Key Takeaway

The significance of the delay $\times$ bandwidth product is that it represents the amount of data that could be in transit. We would like to be able to send this much data without waiting for the first acknowledgment. The principle at work here is often referred to as keeping the pipe full. The algorithms presented in the following two subsections do exactly this.

Sliding Window

Consider again the scenario in which the link has a delay $\times$ bandwidth product of 8 KB and frames are 1 KB in size. We would like the sender to be ready to transmit the ninth frame at pretty much the same moment that the ACK for the first frame arrives. The algorithm that allows us to do this is called sliding window, and an illustrative timeline is given in Figure 3.

Timeline for the sliding window algorithm.

The Sliding Window Algorithm

The sliding window algorithm works as follows. First, the sender assigns a sequence number, denoted SeqNum, to each frame. For now, let's ignore the fact that SeqNum is implemented by a finite-size header field and instead assume that it can grow infinitely large. The sender maintains three variables: The send window size, denoted SWS, gives the upper bound on the number of outstanding (unacknowledged) frames that the sender can transmit; LAR denotes the sequence number of the last acknowledgment received; and LFS denotes the sequence number of the last frame sent. The sender also maintains the following invariant:

LFS - LAR <= SWS

This situation is illustrated in Figure 4.

Sliding window on sender.

When an acknowledgment arrives, the sender moves LAR to the right, thereby allowing the sender to transmit another frame. Also, the sender associates a timer with each frame it transmits, and it retransmits the frame should the timer expire before an ACK is received. Notice that the sender has to be willing to buffer up to SWS frames since it must be prepared to retransmit them until they are acknowledged.

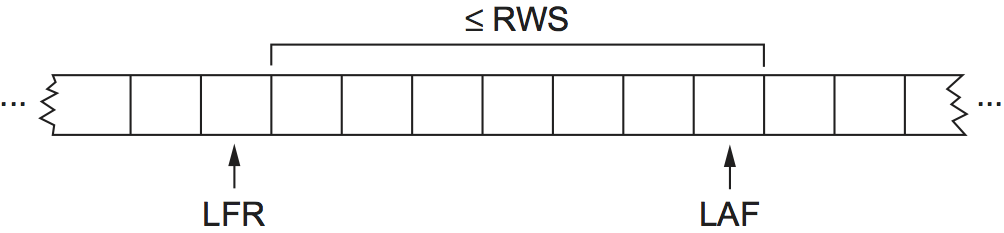
The receiver maintains the following three variables: The receive window size, denoted RWS, gives the upper bound on the number of out-of-order frames that the receiver is willing to accept; LAF denotes the sequence number of the largest acceptable frame; and LFR denotes the sequence number of the last frame received. The receiver also maintains the following invariant:

LAF - LFR <= RWS

This situation is illustrated in Figure 5.

Sliding window on receiver.

When a frame with sequence number SeqNum arrives, the receiver takes the following action. If SeqNum <= LFR or SeqNum > LAF, then the frame is outside the receiver's window and it is discarded. If LFR < SeqNum <= LAF, then the frame is within the receiver's window and it is accepted. Now the receiver needs to decide whether or not to send an ACK. Let SeqNumToAck denote the largest sequence number not yet acknowledged, such that all frames with sequence numbers less than or equal to SeqNumToAck have been received. The receiver acknowledges the receipt of SeqNumToAck, even if higher numbered packets have been received. This acknowledgment is said to be cumulative. It then sets LFR = SeqNumToAck and adjusts LAF = LFR + RWS.

For example, suppose LFR = 5 (i.e., the last ACK the receiver sent was for sequence number 5), and RWS = 4. This implies that LAF = 9. Should frames 7 and 8 arrive, they will be buffered because they are within the receiver's window. However, no ACK needs to be sent since frame 6 has yet to arrive. Frames 7 and 8 are said to have arrived out of order. (Technically, the receiver could resend an ACK for frame 5 when frames 7 and 8 arrive.) Should frame 6 then arrive—perhaps it is late because it was lost the first time and had to be retransmitted, or perhaps it was simply delayed—the receiver acknowledges frame 8, bumps LFR to 8, and sets LAF to 12. If frame 6 was in fact lost, then a timeout will have occurred at the sender, causing it to retransmit frame 6.

It's unlikely that a packet could be delayed on a point-to-point link, this same algorithm is used on multi-hop connections where such delays are possible.

We observe that when a timeout occurs, the amount of data in transit decreases, since the sender is unable to advance its window until frame 6 is acknowledged. This means that when packet losses occur, this scheme is no longer keeping the pipe full. The longer it takes to notice that a packet loss has occurred, the more severe this problem becomes.

Notice that, in this example, the receiver could have sent a negative acknowledgment (NAK) for frame 6 as soon as frame 7 arrived. However, this is unnecessary since the sender's timeout mechanism is sufficient to catch this situation, and sending NAKs adds additional complexity to the receiver. Also, as we mentioned, it would have been legitimate to send additional acknowledgments of frame 5 when frames 7 and 8 arrived; in some cases, a sender can use duplicate ACKs as a clue that a frame was lost. Both approaches help to improve performance by allowing early detection of packet losses.

Yet another variation on this scheme would be to use selective acknowledgments. That is, the receiver could acknowledge exactly those frames it has received rather than just the highest numbered frame received in order. So, in the above example, the receiver could acknowledge the receipt of frames 7 and 8. Giving more information to the sender makes it potentially easier for the sender to keep the pipe full but adds complexity to the implementation.

The sending window size is selected according to how many frames we want to have outstanding on the link at a given time; SWS is easy to compute for a given delay $\times$ bandwidth product. On the other hand, the receiver can set RWS to whatever it wants. Two common settings are RWS = 1, which implies that the receiver will not buffer any frames that arrive out of order, and RWS = SWS, which implies that the receiver can buffer any of the frames the sender transmits. It makes no sense to set RWS > SWS since it's impossible for more than SWS frames to arrive out of order.

Finite Sequence Numbers and Sliding Window

We now return to the one simplification we introduced into the algorithm—our assumption that sequence numbers can grow infinitely large. In practice, of course, a frame's sequence number is specified in a header field of some finite size. For example, a 3-bit field means that there are eight possible sequence numbers, 0..7. This makes it necessary to reuse sequence numbers or, stated another way, sequence numbers wrap around. This introduces the problem of being able to distinguish between different incarnations of the same sequence numbers, which implies that the number of possible sequence numbers must be larger than the number of outstanding frames allowed. For example, stop-and-wait allowed one outstanding frame at a time and had two distinct sequence numbers.

Suppose we have one more number in our space of sequence numbers than we have potentially outstanding frames; that is, SWS <= MaxSeqNum - 1, where MaxSeqNum is the number of available sequence numbers. Is this sufficient? The answer depends on RWS. If RWS = 1, then MaxSeqNum >= SWS + 1 is sufficient. If RWS is equal to SWS, then having a MaxSeqNum just one greater than the sending window size is not good enough. To see this, consider the situation in which we have the eight sequence numbers 0 through 7, and SWS = RWS = 7. Suppose the sender transmits frames 0..6, they are successfully received, but the ACKs are lost. The receiver is now expecting frames 7, 0..5, but the sender times out and sends frames 0..6. Unfortunately, the receiver is expecting the second incarnation of frames 0..5 but gets the first incarnation of these frames. This is exactly the situation we wanted to avoid.

It turns out that the sending window size can be no more than half as big as the number of available sequence numbers when RWS = SWS, or stated more precisely,

SWS < (MaxSeqNum + 1)/ 2

Intuitively, what this is saying is that the sliding window protocol alternates between the two halves of the sequence number space, just as stop-and-wait alternates between sequence numbers 0 and 1. The only difference is that it continually slides between the two halves rather than discretely alternating between them.

Note that this rule is specific to the situation where RWS = SWS. We leave it as an exercise to determine the more general rule that works for arbitrary values of RWS and SWS. Also note that the relationship between the window size and the sequence number space depends on an assumption that is so obvious that it is easy to overlook, namely that frames are not reordered in transit. This cannot happen on a direct point-to-point link since there is no way for one frame to overtake another during transmission. However, we will see the sliding window algorithm used in a different environments, and we will need to devise another rule.

Implementation of Sliding Window

The following routines illustrate how we might implement the sending and receiving sides of the sliding window algorithm. The routines are taken from a working protocol named, appropriately enough, Sliding Window Protocol (SWP). So as not to concern ourselves with the adjacent protocols in the protocol graph, we denote the protocol sitting above SWP as the high-level protocol (HLP) and the protocol sitting below SWP as the link-level protocol (LLP).

We start by defining a pair of data structures. First, the frame header is very simple: It contains a sequence number (SeqNum) and an acknowledgment number (AckNum). It also contains a Flags field that indicates whether the frame is an ACK or carries data.

typedef u_char SwpSeqno;

typedef struct {
    SwpSeqno   SeqNum;   /* sequence number of this frame */
    SwpSeqno   AckNum;   /* ack of received frame */
    u_char     Flags;           /* up to 8 bits worth of flags */
} SwpHdr;

Next, the state of the sliding window algorithm has the following structure. For the sending side of the protocol, this state includes variables LAR and LFS, as described earlier in this section, as well as a queue that holds frames that have been transmitted but not yet acknowledged (sendQ). The sending state also includes a counting semaphore called sendWindowNotFull. We will see how this is used below, but generally a semaphore is a synchronization primitive that supports semWait and semSignal operations. Every invocation of semSignal increments the semaphore by 1, and every invocation of semWait decrements s by 1, with the calling process blocked (suspended) should decrementing the semaphore cause its value to become less than 0. A process that is blocked during its call to semWait will be allowed to resume as soon as enough semSignal operations have been performed to raise the value of the semaphore above 0.

For the receiving side of the protocol, the state includes the variable NFE. This is the next frame expected, the frame with a sequence number one more that the last frame received (LFR), described earlier in this section. There is also a queue that holds frames that have been received out of order (recvQ). Finally, although not shown, the sender and receiver sliding window sizes are defined by constants SWS and RWS, respectively.

typedef struct {
    /* sender side state: */
    SwpSeqno    LAR;        /* seqno of last ACK received */
    SwpSeqno    LFS;        /* last frame sent */
    Semaphore   sendWindowNotFull;
    SwpHdr      hdr;        /* pre-initialized header */
    struct sendQ_slot {
        Event   timeout;    /* event associated with send-timeout */
        Msg     msg;
    }   sendQ[SWS];

    /* receiver side state: */
    SwpSeqno    NFE;       /* seqno of next frame expected */
    struct recvQ_slot {
        int     received;  /* is msg valid? */
        Msg     msg;
    }   recvQ[RWS];
} SwpState;

The sending side of SWP is implemented by procedure sendSWP. This routine is rather simple. First, semWait causes this process to block on a semaphore until it is OK to send another frame. Once allowed to proceed, sendSWP sets the sequence number in the frame's header, saves a copy of the frame in the transmit queue (sendQ), schedules a timeout event to handle the case in which the frame is not acknowledged, and sends the frame to the next-lower-level protocol, which we denote as LINK.

One detail worth noting is the call to store_swp_hdr just before the call to msgAddHdr. This routine translates the C structure that holds the SWP header (state->hdr) into a byte string that can be safely attached to the front of the message (hbuf). This routine (not shown) must translate each integer field in the header into network byte order and remove any padding that the compiler has added to the C structure. The issue of byte order is a non-trivial issue, but for now it is enough to assume that this routine places the most significant bit of a multiword integer in the byte with the highest address.

Another piece of complexity in this routine is the use of semWait and the sendWindowNotFull semaphore. sendWindowNotFull is initialized to the size of the sender's sliding window, SWS (this initialization is not shown). Each time the sender transmits a frame, the semWait operation decrements this count and blocks the sender should the count go to 0. Each time an ACK is received, the semSignal operation invoked in deliverSWP (see below) increments this count, thus unblocking any waiting sender.

static int 
sendSWP(SwpState *state, Msg *frame) 
{
    struct sendQ_slot *slot;
    hbuf[HLEN];

    /* wait for send window to open */
    semWait(&state->sendWindowNotFull);
    state->hdr.SeqNum = ++state->LFS;
    slot = &state->sendQ[state->hdr.SeqNum % SWS];
    store_swp_hdr(state->hdr, hbuf);
    msgAddHdr(frame, hbuf, HLEN);
    msgSaveCopy(&slot->msg, frame);
    slot->timeout = evSchedule(swpTimeout, slot, SWP_SEND_TIMEOUT);
    return send(LINK, frame);
}

Before continuing to the receive side of SWP, we need to reconcile a seeming inconsistency. On the one hand, we have been saying that a high-level protocol invokes the services of a low-level protocol by calling the send operation, so we would expect that a protocol that wants to send a message via SWP would call send(SWP, packet). On the other hand, the procedure that implements SWP's send operation is called sendSWP, and its first argument is a state variable (SwpState). What gives? The answer is that the operating system provides glue code that translates the generic call to send into a protocol-specific call to sendSWP. This glue code maps the first argument to send (the magic protocol variable SWP) into both a function pointer to sendSWP and a pointer to the protocol state that SWP needs to do its job. The reason we have the high-level protocol indirectly invoke the protocol-specific function through the generic function call is that we want to limit how much information the high-level protocol has coded in it about the low-level protocol. This makes it easier to change the protocol graph configuration at some time in the future.

Now we move on to SWP's protocol-specific implementation of the deliver operation, which is given in procedure deliverSWP. This routine actually handles two different kinds of incoming messages: ACKs for frames sent earlier from this node and data frames arriving at this node. In a sense, the ACK half of this routine is the counterpart to the sender side of the algorithm given in sendSWP. A decision as to whether the incoming message is an ACK or a data frame is made by checking the Flags field in the header. Note that this particular implementation does not support piggybacking ACKs on data frames.

When the incoming frame is an ACK, deliverSWP simply finds the slot in the transmit queue (sendQ) that corresponds to the ACK, cancels the timeout event, and frees the frame saved in that slot. This work is actually done in a loop since the ACK may be cumulative. The only other thing to notice about this case is the call to subroutine swpInWindow. This subroutine, which is given below, ensures that the sequence number for the frame being acknowledged is within the range of ACKs that the sender currently expects to receive.

When the incoming frame contains data, deliverSWP first calls msgStripHdr and load_swp_hdr to extract the header from the frame. Routine load_swp_hdr is the counterpart to store_swp_hdr discussed earlier; it translates a byte string into the C data structure that holds the SWP header. deliverSWP then calls swpInWindow to make sure the sequence number of the frame is within the range of sequence numbers that it expects. If it is, the routine loops over the set of consecutive frames it has received and passes them up to the higher-level protocol by invoking the deliverHLP routine. It also sends a cumulative ACK back to the sender, but does so by looping over the receive queue (it does not use the SeqNumToAck variable used in the prose description given earlier in this section).

static int 
deliverSWP(SwpState state, Msg *frame) 
{
    SwpHdr   hdr;
    char     *hbuf;

    hbuf = msgStripHdr(frame, HLEN);
    load_swp_hdr(&hdr, hbuf) 
    if (hdr->Flags & FLAG_ACK_VALID) 
    {
        /* received an acknowledgment—do SENDER side */
        if (swpInWindow(hdr.AckNum, state->LAR + 1, state->LFS)) 
        {
            do 
            {
                struct sendQ_slot *slot;

                slot = &state->sendQ[++state->LAR % SWS];
                evCancel(slot->timeout);
                msgDestroy(&slot->msg);
                semSignal(&state->sendWindowNotFull);
            } while (state->LAR != hdr.AckNum);
        }
    }

    if (hdr.Flags & FLAG_HAS_DATA) 
    {
        struct recvQ_slot *slot;

        /* received data packet—do RECEIVER side */
        slot = &state->recvQ[hdr.SeqNum % RWS];
        if (!swpInWindow(hdr.SeqNum, state->NFE, state->NFE + RWS - 1)) 
        {
            /* drop the message */
            return SUCCESS;
        }
        msgSaveCopy(&slot->msg, frame);
        slot->received = TRUE;
        if (hdr.SeqNum == state->NFE) 
        {
            Msg m;

            while (slot->received) 
            {
                deliver(HLP, &slot->msg);
                msgDestroy(&slot->msg);
                slot->received = FALSE;
                slot = &state->recvQ[++state->NFE % RWS];
            }
            /* send ACK: */
            prepare_ack(&m, state->NFE - 1);
            send(LINK, &m);
            msgDestroy(&m);
        }
    }
    return SUCCESS;
}

Finally,swpInWindow is a simple subroutine that checks to see if a given sequence number falls between some minimum and maximum sequence number.

static bool 
swpInWindow(SwpSeqno seqno, SwpSeqno min, SwpSeqno max) 
{
    SwpSeqno pos, maxpos;

    pos    = seqno - min;       /* pos *should* be in range [0..MAX) */
    maxpos = max - min + 1;     /* maxpos is in range [0..MAX] */
    return pos < maxpos;
}

Frame Order and Flow Control

The sliding window protocol is perhaps the best known algorithm in computer networking. What is easily confused about the algorithm, however, is that it can be used to serve three different roles. The first role is the one we have been concentrating on in this section—to reliably deliver frames across an unreliable link. (In general, the algorithm can be used to reliably deliver messages across an unreliable network.) This is the core function of the algorithm.

The second role that the sliding window algorithm can serve is to preserve the order in which frames are transmitted. This is easy to do at the receiver—since each frame has a sequence number, the receiver just makes sure that it does not pass a frame up to the next-higher-level protocol until it has already passed up all frames with a smaller sequence number. That is, the receiver buffers (i.e., does not pass along) out-of-order frames. The version of the sliding window algorithm described in this section does preserve frame order, although we could imagine a variation in which the receiver passes frames to the next protocol without waiting for all earlier frames to be delivered. A question we should ask ourselves is whether we really need the sliding window protocol to keep the frames in order at the link level, or whether, instead, this functionality should be implemented by a protocol higher in the stack.

The third role that the sliding window algorithm sometimes plays is to support flow control—a feedback mechanism by which the receiver is able to throttle the sender. Such a mechanism is used to keep the sender from over-running the receiver—that is, from transmitting more data than the receiver is able to process. This is usually accomplished by augmenting the sliding window protocol so that the receiver not only acknowledges frames it has received but also informs the sender of how many frames it has room to receive. The number of frames that the receiver is capable of receiving corresponds to how much free buffer space it has. As in the case of ordered delivery, we need to make sure that flow control is necessary at the link level before incorporating it into the sliding window protocol.

Key Takeaway

One important concept to take away from this discussion is the system design principle we call separation of concerns. That is, you must be careful to distinguish between different functions that are sometimes rolled together in one mechanism, and you must make sure that each function is necessary and being supported in the most effective way. In this particular case, reliable delivery, ordered delivery, and flow control are sometimes combined in a single sliding window protocol, and we should ask ourselves if this is the right thing to do at the link level.

Concurrent Logical Channels

The data link protocol used in the original ARPANET provides an interesting alternative to the sliding window protocol, in that it is able to keep the pipe full while still using the simple stop-and-wait algorithm. One important consequence of this approach is that the frames sent over a given link are not kept in any particular order. The protocol also implies nothing about flow control.

The idea underlying the ARPANET protocol, which we refer to as concurrent logical channels, is to multiplex several logical channels onto a single point-to-point link and to run the stop-and-wait algorithm on each of these logical channels. There is no relationship maintained among the frames sent on any of the logical channels, yet because a different frame can be outstanding on each of the several logical channels the sender can keep the link full.

More precisely, the sender keeps 3 bits of state for each channel: a boolean, saying whether the channel is currently busy; the 1-bit sequence number to use the next time a frame is sent on this logical channel; and the next sequence number to expect on a frame that arrives on this channel. When the node has a frame to send, it uses the lowest idle channel, and otherwise it behaves just like stop-and-wait.

In practice, the ARPANET supported 8 logical channels over each ground link and 16 over each satellite link. In the ground-link case, the header for each frame included a 3-bit channel number and a 1-bit sequence number, for a total of 4 bits. This is exactly the number of bits the sliding window protocol requires to support up to 8 outstanding frames on the link when RWS = SWS.