6.2: Queuing Disciplines
- Page ID
- 13975
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.2 Queuing Disciplines
6.2 Queuing Disciplines
Regardless of how simple or how sophisticated the rest of the resource allocation mechanism is, each router must implement some queuing discipline that governs how packets are buffered while waiting to be transmitted. The queuing algorithm can be thought of as allocating both bandwidth (which packets get transmitted) and buffer space (which packets get discarded). It also directly affects the latency experienced by a packet by determining how long a packet waits to be transmitted. This section introduces two common queuing algorithms—first-in, first-out (FIFO) and fair queuing (FQ)—and identifies several variations that have been proposed.
FIFO
The idea of FIFO queuing, also called first-come, first-served (FCFS) queuing, is simple: The first packet that arrives at a router is the first packet to be transmitted. This is illustrated in Figure 1(a), which shows a FIFO with "slots" to hold up to eight packets. Given that the amount of buffer space at each router is finite, if a packet arrives and the queue (buffer space) is full, then the router discards that packet, as shown in Figure 1(b). This is done without regard to which flow the packet belongs to or how important the packet is. This is sometimes called tail drop, since packets that arrive at the tail end of the FIFO are dropped.
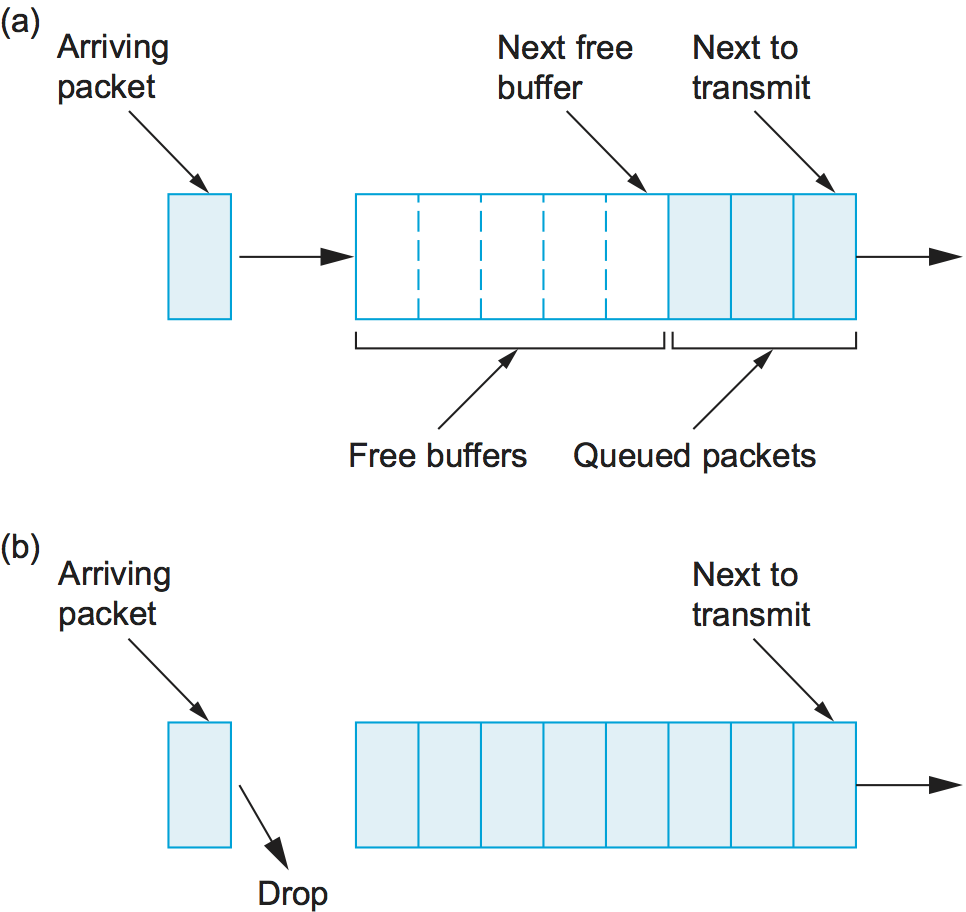
Note that tail drop and FIFO are two separable ideas. FIFO is a scheduling discipline—it determines the order in which packets are transmitted. Tail drop is a drop policy—it determines which packets get dropped. Because FIFO and tail drop are the simplest instances of scheduling discipline and drop policy, respectively, they are sometimes viewed as a bundle—the vanilla queuing implementation. Unfortunately, the bundle is often referred to simply as FIFO queuing, when it should more precisely be called FIFO with tail drop. A later section provides an example of another drop policy, which uses a more complex algorithm than "Is there a free buffer?" to decide when to drop packets. Such a drop policy may be used with FIFO, or with more complex scheduling disciplines.
FIFO with tail drop, as the simplest of all queuing algorithms, is the most widely used in Internet routers at the time of writing. This simple approach to queuing pushes all responsibility for congestion control and resource allocation out to the edges of the network. Thus, the prevalent form of congestion control in the Internet currently assumes no help from the routers: TCP takes responsibility for detecting and responding to congestion. We will see how this works in the next section.
A simple variation on basic FIFO queuing is priority queuing. The idea is to mark each packet with a priority; the mark could be carried, for example, in the IP header, as we'll discuss in a later section. The routers then implement multiple FIFO queues, one for each priority class. The router always transmits packets out of the highest-priority queue if that queue is nonempty before moving on to the next priority queue. Within each priority, packets are still managed in a FIFO manner. This idea is a small departure from the best-effort delivery model, but it does not go so far as to make guarantees to any particular priority class. It just allows high-priority packets to cut to the front of the line.
The problem with priority queuing, of course, is that the high-priority queue can starve out all the other queues; that is, as long as there is at least one high-priority packet in the high-priority queue, lower-priority queues do not get served. For this to be viable, there needs to be hard limits on how much high-priority traffic is inserted in the queue. It should be immediately clear that we can't allow users to set their own packets to high priority in an uncontrolled way; we must either prevent them from doing this altogether or provide some form of "pushback" on users. One obvious way to do this is to use economics—the network could charge more to deliver high-priority packets than low-priority packets. However, there are significant challenges to implementing such a scheme in a decentralized environment such as the Internet.
One situation in which priority queuing is used in the Internet is to protect the most important packets—typically, the routing updates that are necessary to stabilize the routing tables after a topology change. Often there is a special queue for such packets, which can be identified by the Differentiated Services Code Point (formerly the TOS field) in the IP header. This is in fact a simple case of the idea of "Differentiated Services."
Fair Queuing
The main problem with FIFO queuing is that it does not discriminate between different traffic sources, or, in the language introduced in the previous section, it does not separate packets according to the flow to which they belong. This is a problem at two different levels. At one level, it is not clear that any congestion-control algorithm implemented entirely at the source will be able to adequately control congestion with so little help from the routers. We will suspend judgment on this point until the next section when we discuss TCP congestion control. At another level, because the entire congestion-control mechanism is implemented at the sources and FIFO queuing does not provide a means to police how well the sources adhere to this mechanism, it is possible for an ill-behaved source (flow) to capture an arbitrarily large fraction of the network capacity. Considering the Internet again, it is certainly possible for a given application not to use TCP and, as a consequence, to bypass its end-to-end congestion-control mechanism. (Applications such as Internet telephony do this today.) Such an application is able to flood the Internet's routers with its own packets, thereby causing other applications' packets to be discarded.
Fair queuing (FQ) is an algorithm that has been designed to address this problem. The idea of FQ is to maintain a separate queue for each flow currently being handled by the router. The router then services these queues in a sort of round-robin, as illustrated in Figure 2. When a flow sends packets too quickly, then its queue fills up. When a queue reaches a particular length, additional packets belonging to that flow's queue are discarded. In this way, a given source cannot arbitrarily increase its share of the network's capacity at the expense of other flows.
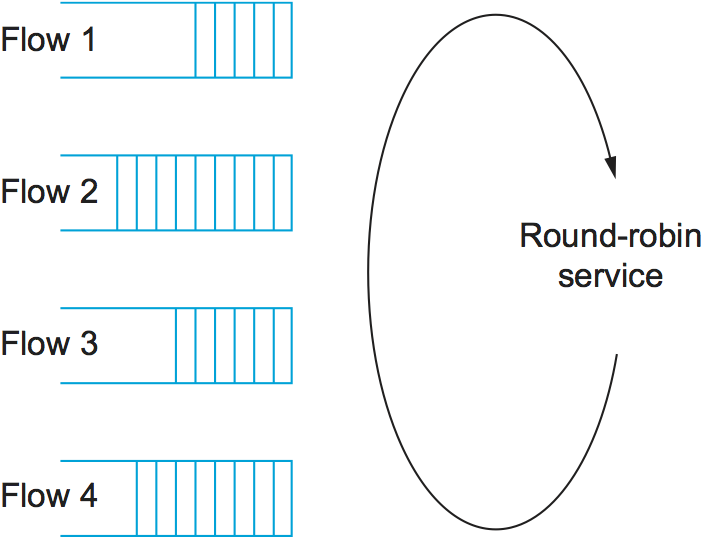
Note that FQ does not involve the router telling the traffic sources anything about the state of the router or in any way limiting how quickly a given source sends packets. In other words, FQ is still designed to be used in conjunction with an end-to-end congestion-control mechanism. It simply segregates traffic so that ill-behaved traffic sources do not interfere with those that are faithfully implementing the end-to-end algorithm. FQ also enforces fairness among a collection of flows managed by a well-behaved congestion-control algorithm.
As simple as the basic idea is, there are still a modest number of details that you have to get right. The main complication is that the packets being processed at a router are not necessarily the same length. To truly allocate the bandwidth of the outgoing link in a fair manner, it is necessary to take packet length into consideration. For example, if a router is managing two flows, one with 1000-byte packets and the other with 500-byte packets (perhaps because of fragmentation upstream from this router), then a simple round-robin servicing of packets from each flow's queue will give the first flow two-thirds of the link's bandwidth and the second flow only one-third of its bandwidth.
What we really want is bit-by-bit round-robin, where the router transmits a bit from flow 1, then a bit from flow 2, and so on. Clearly, it is not feasible to interleave the bits from different packets. The FQ mechanism therefore simulates this behavior by first determining when a given packet would finish being transmitted if it were being sent using bit-by-bit round-robin and then using this finishing time to sequence the packets for transmission.
To understand the algorithm for approximating bit-by-bit round-robin, consider the behavior of a single flow and imagine a clock that ticks once each time one bit is transmitted from all of the active flows. (A flow is active when it has data in the queue.) For this flow, let denote the length of packet , let denote the time when the router starts to transmit packet , and let denote the time when the router finishes transmitting packet . If is expressed in terms of how many clock ticks it takes to transmit packet (keeping in mind that time advances 1 tick each time this flow gets 1 bit's worth of service), then it is easy to see that .
When do we start transmitting packet ? The answer to this question depends on whether packet arrived before or after the router finished transmitting packet from this flow. If it was before, then logically the first bit of packet is transmitted immediately after the last bit of packet . On the other hand, it is possible that the router finished transmitting packet long before arrived, meaning that there was a period of time during which the queue for this flow was empty, so the round-robin mechanism could not transmit any packets from this flow. If we let denote the time that packet arrives at the router, then . Thus, we can compute
Now we move on to the situation in which there is more than one flow, and we find that there is a catch to determining . We can't just read the wall clock when the packet arrives. As noted above, we want time to advance by one tick each time all the active flows get one bit of service under bit-by-bit round-robin, so we need a clock that advances more slowly when there are more flows. Specifically, the clock must advance by one tick when bits are transmitted if there are active flows. This clock will be used to calculate .
Now, for every flow, we calculate for each packet that arrives using the above formula. We then treat all the as timestamps, and the next packet to transmit is always the packet that has the lowest timestamp—the packet that, based on the above reasoning, should finish transmission before all others.
Note that this means that a packet can arrive on a flow, and, because it is shorter than a packet from some other flow that is already in the queue waiting to be transmitted, it can be inserted into the queue in front of that longer packet. However, this does not mean that a newly arriving packet can preempt a packet that is currently being transmitted. It is this lack of preemption that keeps the implementation of FQ just described from exactly simulating the bit-by-bit round-robin scheme that we are attempting to approximate.
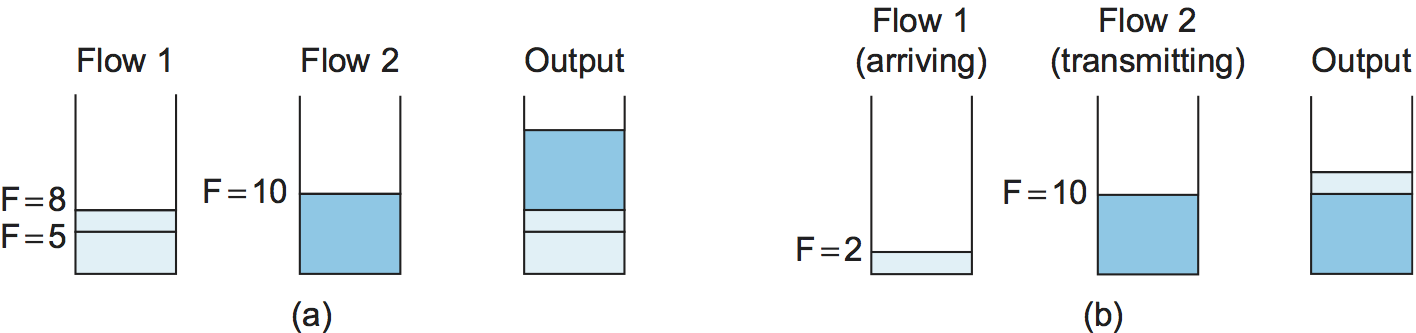
To better see how this implementation of fair queuing works, consider the example given in Figure 3. Part (a) shows the queues for two flows; the algorithm selects both packets from flow 1 to be transmitted before the packet in the flow 2 queue, because of their earlier finishing times. In (b), the router has already begun to send a packet from flow 2 when the packet from flow 1 arrives. Though the packet arriving on flow 1 would have finished before flow 2 if we had been using perfect bit-by-bit fair queuing, the implementation does not preempt the flow 2 packet.
There are two things to notice about fair queuing. First, the link is never left idle as long as there is at least one packet in the queue. Any queuing scheme with this characteristic is said to be work conserving. One effect of being work conserving is that if I am sharing a link with a lot of flows that are not sending any data then; I can use the full link capacity for my flow. As soon as the other flows start sending, however, they will start to use their share and the capacity available to my flow will drop.
The second thing to notice is that if the link is fully loaded and there are flows sending data, I cannot use more than of the link bandwidth. If I try to send more than that, my packets will be assigned increasingly large timestamps, causing them to sit in the queue longer awaiting transmission. Eventually, the queue will overflow—although whether it is my packets or someone else's that are dropped is a decision that is not determined by the fact that we are using fair queuing. This is determined by the drop policy; FQ is a scheduling algorithm, which, like FIFO, may be combined with various drop policies.
Because FQ is work conserving, any bandwidth that is not used by one flow is automatically available to other flows. For example, if we have four flows passing through a router, and all of them are sending packets, then each one will receive one-quarter of the bandwidth. But, if one of them is idle long enough that all its packets drain out of the router's queue, then the available bandwidth will be shared among the remaining three flows, which will each now receive one-third of the bandwidth. Thus, we can think of FQ as providing a guaranteed minimum share of bandwidth to each flow, with the possibility that it can get more than its guarantee if other flows are not using their shares.
It is possible to implement a variation of FQ, called weighted fair queuing (WFQ), that allows a weight to be assigned to each flow (queue). This weight logically specifies how many bits to transmit each time the router services that queue, which effectively controls the percentage of the link's bandwidth that that flow will get. Simple FQ gives each queue a weight of 1, which means that logically only 1 bit is transmitted from each queue each time around. This results in each flow getting of the bandwidth when there are flows. With WFQ, however, one queue might have a weight of 2, a second queue might have a weight of 1, and a third queue might have a weight of 3. Assuming that each queue always contains a packet waiting to be transmitted, the first flow will get one-third of the available bandwidth, the second will get one-sixth of the available bandwidth, and the third will get one-half of the available bandwidth.
While we have described WFQ in terms of flows, note that it could be implemented on classes of traffic, where classes are defined in some other way than the simple flows introduced at the start of this chapter. For example, we could use some bits in the IP header to identify classes and allocate a queue and a weight to each class. This is exactly what is proposed as part of the Differentiated Services architecture described in a later section.
Note that a router performing WFQ must learn what weights to assign to each queue from somewhere, either by manual configuration or by some sort of signalling from the sources. In the latter case, we are moving toward a reservation-based model. Just assigning a weight to a queue provides a rather weak form of reservation because these weights are only indirectly related to the bandwidth the flow receives. (The bandwidth available to a flow also depends, for example, on how many other flows are sharing the link.) We will see in a later section how WFQ can be used as a component of a reservation-based resource allocation mechanism.
Key Takeaway
Finally, we observe that this whole discussion of queue management illustrates an important system design principle known as separating policy and mechanism. The idea is to view each mechanism as a black box that provides a multifaceted service that can be controlled by a set of knobs. A policy specifies a particular setting of those knobs but does not know (or care) about how the black box is implemented. In this case, the mechanism in question is the queuing discipline, and the policy is a particular setting of which flow gets what level of service (e.g., priority or weight). We discuss some policies that can be used with the WFQ mechanism in a later section.

