14.6: Two’s Complement of a Number

Last updated
Save as PDF

Page ID: 43748

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Now we have all the pieces of the puzzle: we know how we can encode positive and negative numbers, we know how to use the complement to turn a subtraction into an addition. Let us see how the 2’s complement is used to negate numbers and perform subtraction.

The 2’s complement is a common method to represent signed integers. The advantages are that addition and subtraction are implemented without having to check the sign of the operands and 2’s complement has only one representation for zero (avoiding negative zero). Adding numbers of different sign encoded using 2’s complement does not require any special processing: the sign of the result is determined automatically. The 2’s complement of a positive number represents the negative form of that number.

What the 10’s complement shows us is that it is computed by taking the difference of each digit with the largest number available in the base system, 9 in decimal base and adding one. Now in the case of binary, the largest number is one. Due to the fact that \( 1 - 0 = 1 \) and \( 1 - 1 = 0 \), computing the 2’s complement of number is exactly the same as flipping 1’s to 0’s and vice versa and adding 1.

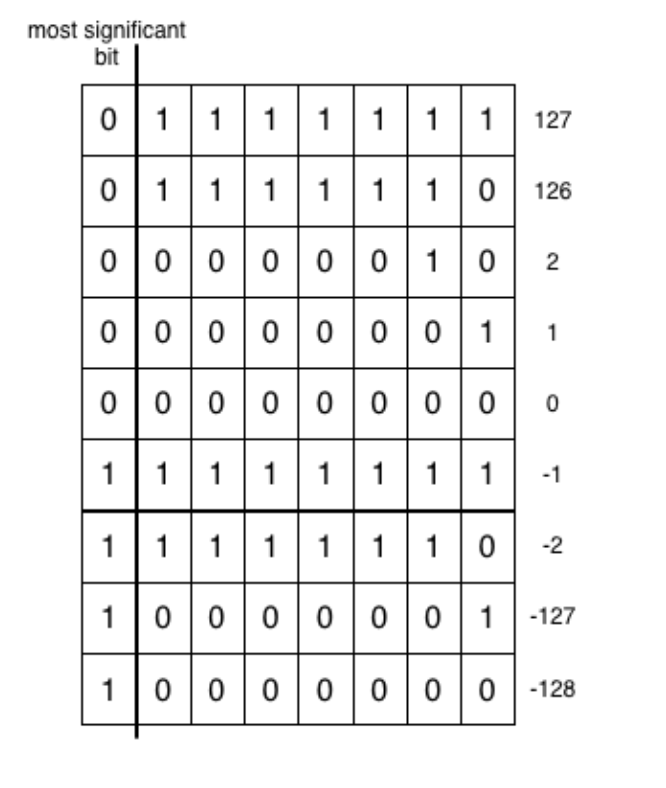
Let’s look at the number 2. It is encoded on 8 bits as 000000010 and −2 as 11111110 as shown in Figure \(\PageIndex{1}\). 000000010 flipped is: 11111101 and we add one: so we get 11111110. The difference between -2 (11111110) and 126 (01111110) is given by the most significant bit which conveys the integer sign.

Two's complement in 8 bits. — Figure \(\PageIndex{1}\): *Overview of two's complement on 8 bits.*

Try the following expressions in Pharo and experiment with them. We compute the direct inversion (bitwise NOT) and add one. Remember a bitwise NOT is turning any 1s into 0s and conversely. You can use the bitString message to obtain the bit representation of a number. If you check the length of the printed results, you will notice that they are 31 bits long instead of 32. This is because in Pharo and most Smalltalk implementations, small integers are specially encoded and this encoding requires one bit.

2 bitString
    '0000000000000000000000000000010'
2 bitInvert bitString
    '1111111111111111111111111111101'
(2 bitInvert + 1) bitString
    '1111111111111111111111111111110'
-2 bitString
    '1111111111111111111111111111110'

Note that the 2’s complement of a negative number is the corresponding positive value as shown by the following expressions: -2 two complement is 2. First we compute the direct inversion (bitwise NOT) and add one.

-2 bitString
    → '1111111111111111111111111111110'
-2 bitInvert bitString
    → '0000000000000000000000000000001'
(-2 bitInvert + 1) bitString
    → '0000000000000000000000000000010'
2 bitString
    → '0000000000000000000000000000010'

As you see negating a number and computing its two’s complement gives the same binary representation.

(2r101 bitInvert + 1) bitString
    returns '1111111111111111111111111111011'
2r101 negated bitString
    returns '1111111111111111111111111111011'

There is one exception. On a given number of bits, let’s say 8 bits as in Figure \(\PageIndex{1}\), we compute the negative of a number by computing its two’s complement (flipping all the bits and adding 1), except for the most negative number. On an 8 bits representation, the most negative number is -128 (1000 0000), inverting it is (0111 1111), and adding one results in itself (1000 0000). We cannot encode 128 on 8 bits signed convention. Here, the carry is "eaten" by the sign bit.

Subtracting. To subtract a number from another one, we just add the second number's 2's complement to the first one.

When we want to compute \( 110110 - 101 \), we compute the 2's complement of 101 and add it. We add 110110 and 111011, and get 110001. This is correct: \( 54 - 5 = 49 \).

110110 - 101
  110110
+ 111011
----------
  110001

Let us test this in Pharo.

(2r110110 - 2r101) bitString
    → '0000000000000000000000000110001'
(2r110110 bitString)
    → '0000000000000000000000000110110'
2r101 bitString
    → '0000000000000000000000000000101'
2r101 negated bitString
    → '1111111111111111111111111111011'

The case where the result is a negative number is also well handled. For example, if we want to compute \( 15 - 35 \), we should get \( -20 \) and this is what we get. Let us see that: 15 is encoded as 0000 1111 and 35 as 0010 0011. Now the two's complement of 35 is 1101 1101.

    0011111 (carry)
    0000 1111
    1101 1101
-----------------
1111111101100

We get well -20.