17.1: Writing Parsers with PetitParser
- Page ID
- 43764
PetitParser is a parsing framework different from many other popular parser generators. PetitParser makes it easy to define parsers with Smalltalk code and to dynamically reuse, compose, transform and extend grammars. We can reflect on the resulting grammars and modify them on-the-fly. As such PetitParser fits better the dynamic nature of Smalltalk.
Furthermore, PetitParser is not based on tables such as SmaCC and ANTLR. Instead it uses a combination of four alternative parser methodologies: scannerless parsers, parser combinators, parsing expression grammars and packrat parsers. As such PetitParser is more powerful in what it can parse. Let’s have a quick look at these four parser methodologies:
Scannerless Parsers combine what is usually done by two independent tools (scanner and parser) into one. This makes writing a grammar much simpler and avoids common problems when grammars are composed.
Parser Combinators are building blocks for parsers modeled as a graph of composable objects; they are modular and maintainable, and can be changed, recomposed, transformed and reflected upon.
Parsing Expression Grammars (PEGs) provide the notion of ordered choices. Unlike parser combinators, the ordered choice of PEGs always follows the first matching alternative and ignores other alternatives. Valid input always results in exactly one parse-tree, the result of a parse is never ambiguous.
Packrat Parsers give linear parse-time guarantees and avoid common problems with left-recursion in PEGs.
Loading PetitParser
Enough talking, let’s get started. PetitParser is developed in Pharo, and there are also versions for Java and Dart available. A ready made image can be downloaded1. To load PetitParser into an existing image evaluate the following Gofer expression:
Code \(\PageIndex{1}\) (Pharo): Installing PetitParser
Gofer new
smalltalkhubUser: 'Moose' project: 'PetitParser';
package: 'ConfigurationOfPetitParser';
load.
(Smalltalk at: #ConfigurationOfPetitParser) perform: #loadDefault.
More information on how to get PetitParser can be found on the chapter about petit parser in the Moose book.2
Writing a simple grammar
Writing grammars with PetitParser is as simple as writing Smalltalk code. For example, to define a grammar that parses identifiers starting with a letter followed by zero or more letters or digits is defined and used as follows:
Code \(\PageIndex{2}\) (Pharo): Creating our first parser to parse identifiers
|identifier| identifier := #letter asParser , #word asParser star. identifier parse: 'a987jlkj' −→ #($a #($9 $8 $7 $j $l $k $j))
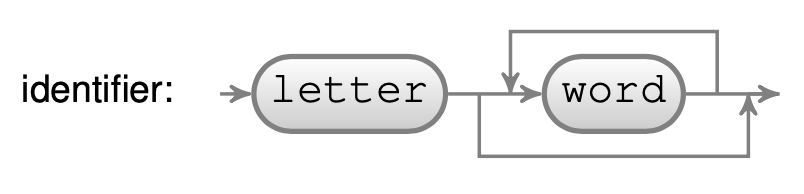
A graphical notation
Figure \(\PageIndex{1}\) presents a syntax diagram of the identifier parser. Each box represents a parser. The arrows between the boxes represent the flow in which input is consumed. The rounded boxes are elementary parsers (terminals). The squared boxes (not shown on this figure) are parsers composed of other parsers (non terminals).
If you inspect the object identifier of the previous script, you’ll notice that it is an instance of a PPSequenceParser. If you dive further into the object you will notice the following tree of different parser objects:
Code \(\PageIndex{3}\) (Pharo): Composition of parsers used for the identifier parser
PPSequenceParser (accepts a sequence of parsers)
PPPredicateObjectParser (accepts a single letter)
PPPossessiveRepeatingParser (accepts zero or more instances of another parser)
PPPredicateObjectParser (accepts a single word character)
The root parser is a sequence parser because the , (comma) operator creates a sequence of (1) a letter parser and (2) zero or more word character parser. The root parser first child is a predicate object parser created by the #letter asParser expression. This parser is capable of parsing a single letter as defined by the Character»isLetter method. The second child is a repeating parser created by the star call. This parser uses its child parser (another predicate object parser) as much as possible on the input (i.e., it is a greedy parser). Its child parser is a predicate object parser created by the #word asParser expression. This parser is capable of parsing a single digit or letter as defined by the Character»isDigit and Character»isLetter methods.
Parsing some input
To actually parse a string (or stream) we use the method PPParser»parse: as follows:
Code \(\PageIndex{4}\) (Pharo): Parsing some input strings with the identifier parser
identifier parse: 'yeah'. → #($y #($e $a $h)) identifier parse: 'f123'. → #($f #($1 $2 $3))
While it seems odd to get these nested arrays with characters as a return value, this is the default decomposition of the input into a parse tree. We’ll see in a while how that can be customized.
If we try to parse something invalid we get an instance of PPFailure as an answer:
Code \(\PageIndex{5}\) (Pharo): Parsing invalid input results in a failure
identifier parse: '123'. → letter expected at 0
This parsing results in a failure because the first character (1) is not a letter. Instances of PPFailure are the only objects in the system that answer with true when you send the message #isPetitFailure. Alternatively you can also use PPParser»parse:onError: to throw an exception in case of an error:
identifier
parse: '123'
onError: [ :msg :pos | self error: msg ].
If you are only interested if a given string (or stream) matches or not you can use the following constructs:
Code \(\PageIndex{6}\) (Pharo): Checking that some inputs are identifiers
identifier matches: 'foo'. → true identifier matches: '123'. → false identifier matches: 'foo()'. → true
The last result can be surprising: indeed, a parenthesis is neither a digit nor a letter as was specified by the #word asParser expression. In fact, the identifier parser matches “foo” and this is enough for the PPParser»matches: call to return true. The result would be similar with the use of parse: which would return #($f #($o $o)).
If you want to be sure that the complete input is matched, use the message PPParser»end as follows:
Code \(\PageIndex{7}\) (Pharo): Ensuring that the whole input is matched using PPParser»end
identifier end matches: 'foo()'. → false
The PPParser»end message creates a new parser that matches the end of input. To be able to compose parsers easily, it is important that parsers do not match the end of input by default. Because of this, you might be interested to find all the places that a parser can match using the message PPParser»matchesSkipIn: and PPParser»matchesIn:.
Code \(\PageIndex{8}\) (Pharo): Finding all matches in an input
identifier matchesSkipIn: 'foo 123 bar12'.
→ an OrderedCollection(#($f #($o $o)) #($b #($a $r $1 $2)))
identifier matchesIn: 'foo 123 bar12'.
→ an OrderedCollection(#($f #($o $o)) #($o #($o)) #($o #()) #($b #($a $r $1 $2))
#($a #($r $1 $2)) #($r #($1 $2)))
The PPParser»matchesSkipIn: method returns a collection of arrays containing what has been matched. This function avoids parsing the same character twice. The method PPParser»matchesIn: does a similar job but returns a collection with all possible sub-parsed elements: e.g., evaluating identifier matchesIn: 'foo 123 bar12' returns a collection of 6 elements.
Similarly, to find all the matching ranges (index of first character and index of last character) in the given input one can use either PPParser»matchingSkipRangesIn: or PPParser»matchingRangesIn: as shown by the script below:
Code \(\PageIndex{9}\) (Pharo): Finding all matched ranges in an input
identifier matchingSkipRangesIn: 'foo 123 bar12'.
→ an OrderedCollection((1 to: 3) (9 to: 13))
identifier matchingRangesIn: 'foo 123 bar12'.
→ an OrderedCollection((1 to: 3) (2 to: 3) (3 to: 3) (9 to: 13) (10 to: 13) (11 to: 13))
Different kinds of parsers
PetitParser provide a large set of ready-made parser that you can compose to consume and transform arbitrarily complex languages. The terminal parsers are the most simple ones. We’ve already seen a few of those, some more are defined in the protocol Table \(\PageIndex{1}\).
| Terminal Parsers | Description |
|---|---|
| $a asParser | Parses the character $a. |
| ’abc’ asParser | Parses the string ’abc’. |
| #any asParser | Parses any character. |
| #digit asParser | Parses one digit (0..9). |
| #letter asParser | Parses one letter (a..z and A..Z). |
| #word asParser | Parses a digit or letter. |
| #blank asParser | Parses a space or a tabulation. |
| #newline asParser | Parses the carriage return or line feed characters. |
| #space asParser | Parses any white space character including new line. |
| #tab asParser | Parses a tab character. |
| #lowercase asParser | Parses a lowercase character. |
| #uppercase asParser | Parses an uppercase character. |
| nil asParser | Parses nothing. |
The class side of PPPredicateObjectParser provides a lot of other factory methods that can be used to build more complex terminal parsers. To use them, send the message PPParser»asParser to a symbol containing the name of the factory method (such as #punctuation asParser).
The next set of parsers are used to combine other parsers together and is defined in the protocol Table \(\PageIndex{2}\).
| Parser Combination | Description |
|---|---|
| p1 , p2 | Parses p1 followed by p2 (sequence). |
| p1 / p2 | Parses p1, if that doesn’t work parses p2. |
| p star | Parses zero or more p. |
| p plus | Parses one or more p. |
| p optional | Parses p if possible. |
| p and | Parses p but does not consume its input. |
| p negate | Parses p and succeeds when p fails. |
| p not | Parses p and succeeds when p fails, but does not consume its input. |
| p end | Parses p and succeeds only at the end of the input. |
| p times: n | Parses p exactly n times. |
| p min: n max: m | Parses p at least n times up to m times |
| p starLazy: q | Like star but stop consuming when q succeeds |
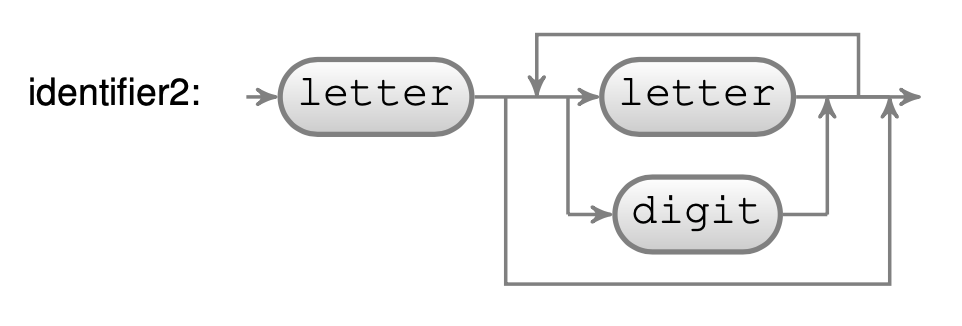
As a simple example of parser combination, the following definition of the identifier2 parser is equivalent to our previous definition of identifier:
Code \(\PageIndex{10}\) (Pharo): A different way to express the identifier parser
identifier2 := #letter asParser , (#letter asParser / #digit asParser) star.
Parser action
To define an action or transformation on a parser we can use one of the messages PPParser»==>, PPParser»flatten, PPParser»token and PPParser»trim defined in the protocol Table \(\PageIndex{3}\).
| Action Parsers | Description |
|---|---|
| p flatten | Creates a string from the result of p. |
| p token | Similar to flatten but returns a PPToken with details. |
| p trim | Trims white spaces before and after p. |
| p trim: trimParser | Trims whatever trimParser can parse (e.g., comments). |
| p ==> aBlock | Performs the transformation given in aBlock. |
To return a string of the parsed identifier instead of getting an array of matched elements, configure the parser by sending it the message PPParser»flatten.
Code \(\PageIndex{11}\) (Pharo): Using flatten so that the parsing result is a string
|identifier| identifier := (#letter asParser , (#letter asParser / #digit asParser) star). identifier parse: 'ajka0' → #($a #($j $k $a $0)) identifier flatten parse: 'ajka0' → 'ajka0'
The message PPParser»token is similar to flatten but returns a PPToken that provide much more contextual information like the collection where the token was located and its position in the collection.
Sending the message PPParser»trim configures the parser to ignore white spaces at the beginning and end of the parsed result. In the following, using the first parser on the input leads to an error because the parser does not accept the spaces. With the second parser, spaces are ignored and removed from the result.

Code \(\PageIndex{12}\) (Pharo): Using PPParser»trim to ignore spaces
|identifier| identifier := (#letter asParser , #word asParser star) flatten. identifier parse: ' ajka ' → letter expected at 0 identifier trim parse: ' ajka ' → 'ajka'
Sending the message trim is equivalent to calling PPParser»trim: with #space asParser as a parameter. That means trim: can be useful to ignore other data from the input, source code comments for example:
Code \(\PageIndex{13}\) (Pharo): Using PPParser»trim: to ignore comments
| identifier comment ignorable line | identifier := (#letter asParser , #word asParser star) flatten. comment := '//' asParser, #newline asParser negate star. ignorable := comment / #space asParser. line := identifier trim: ignorable. line parse: '// This is a comment oneIdentifier // another comment' → 'oneIdentifier'
The message PPParser»==> lets you specify a block to be executed when the parser matches an input. The next section presents several examples. Here is a simple way to get a number from its string representation.
Code \(\PageIndex{14}\) (Pharo): Parsing integers
number := #digit asParser plus flatten ==> [ :str | str asNumber ]. number parse: '123' → 123
The Table \(\PageIndex{3}\) shows the basic elements to build parsers. There are a few more well documented and tested factory methods in the operators protocols of PPParser. If you want to know more about these factory methods, browse these protocols. An interesting one is separatedBy: which answers a new parser that parses the input one or more times, with separations specified by another parser.
Writing a more complicated grammar
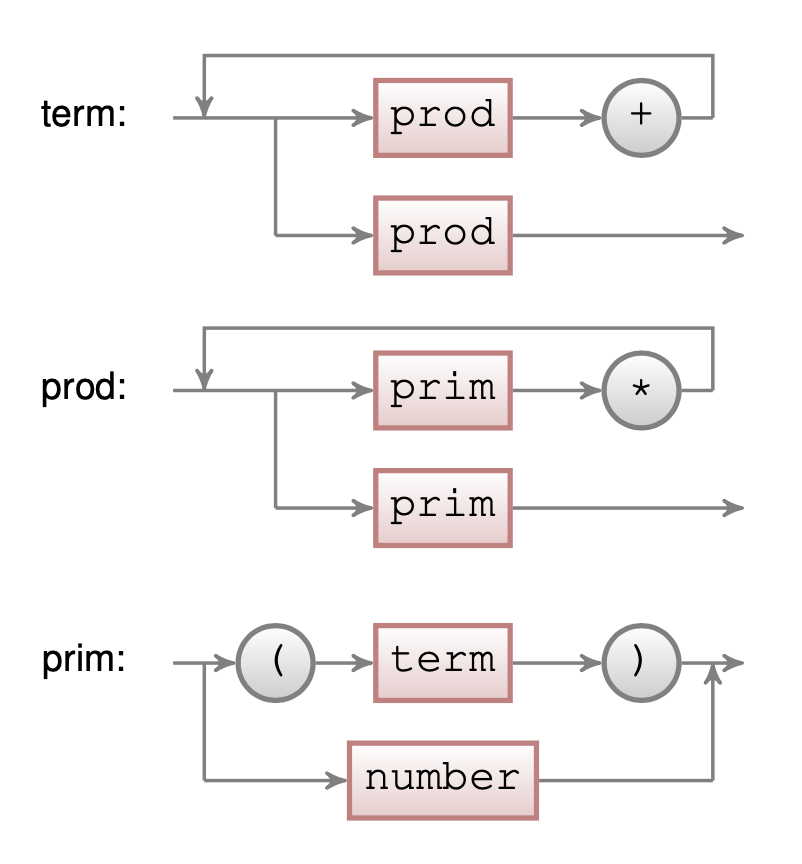
We now write a more complicated grammar for evaluating simple arithmetic expressions. With the grammar for a number (actually an integer) defined above, the next step is to define the productions for addition and multiplication in order of precedence. Note that we instantiate the productions as PPDelegateParser upfront, because they recursively refer to each other. The method #setParser: then resolves this recursion. The following script defines three parsers for the addition, multiplication and parenthesis (see Figure \(\PageIndex{4}\) for the related syntax diagram):
Code \(\PageIndex{15}\) (Pharo): Parsing arithmetic expressions
term := PPDelegateParser new.
prod := PPDelegateParser new.
prim := PPDelegateParser new.
term setParser: (prod , $+ asParser trim , term ==> [ :nodes | nodes first + nodes last ])
/ prod.
prod setParser: (prim , $* asParser trim , prod ==> [ :nodes | nodes first * nodes last ])
/ prim.
prim setParser: ($( asParser trim , term , $) asParser trim ==> [ :nodes | nodes second ])
/ number.
The term parser is defined as being either (1) a prod followed by ‘+’, followed by another term or (2) a prod. In case (1), an action block asks the parser to compute the arithmetic addition of the value of the first node (a prod) and the last node (a term). The prod parser is similar to the term parser. The prim parser is interesting in that it accepts left and right parenthesis before and after a term and has an action block that simply ignores them.
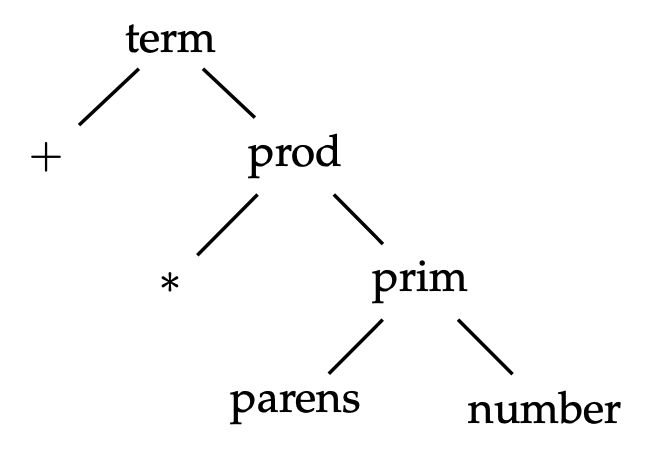
To understand the precedence of productions, see Figure \(\PageIndex{5}\). The root of the tree in this figure (term), is the production that is tried first. A term is either a + or a prod. The term production comes first because + as the lowest priority in mathematics.
To make sure that our parser consumes all input we wrap it with the end parser into the start production:
start := term end.
That’s it, we can now test our parser:
Code \(\PageIndex{16}\) (Pharo): Trying our arithmetic expressions evaluator
start parse: '1 + 2 * 3'. → 7 start parse: '(1 + 2) * 3'. → 9