16.1: The Linked List Data Structure
- Page ID
- 15161
As we said, a static data structure is one whose size is fixed during a program’s execution—a static structure’s memory is allocated at compile time. By contrast, a dynamic structure is one that can grow and shrink as needed. In this section, we will develop a dynamic list, which is a data structure whose elements are arranged in a linear sequence. There is a first element in the list, a second element, and so on. Lists are quite general and, as we will discuss later, lists have a broad range of applications. Depending on how elements are inserted and removed from a list, they can be used for a range of specialized purposes.
16.1.1 Using References to Link Objects
As you know from earlier chapters, when you create an object using the Referring to objects new operator you get back a reference to the object that you then can assign to a reference variable. In the following example, b is a reference to a JButton:
JBu t ton b = new JBu t t on ( ) ;
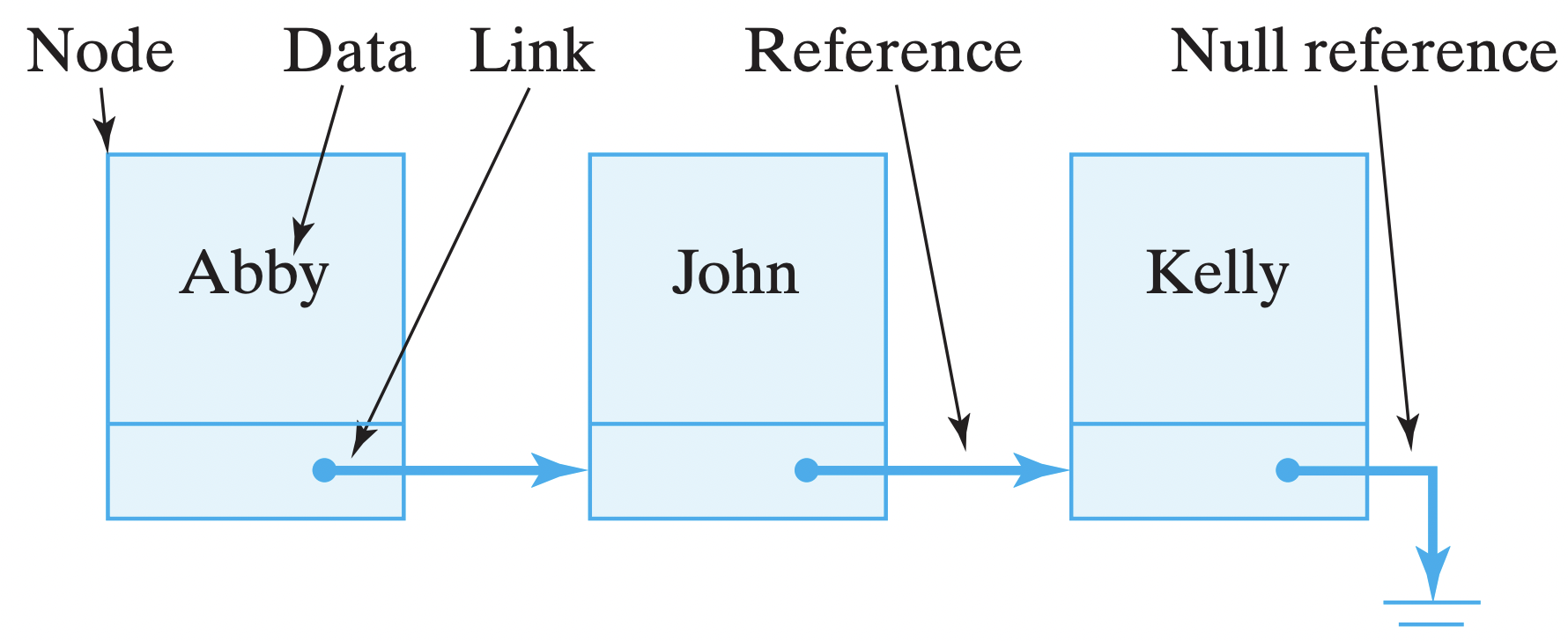
Figure 16.1: A linked list of Nodes terminated by a null link.
We have defined many classes that contained references to other objects:
public class Student {
private String name;
}
In this example, name is a reference to a String object.
A linked list is a list in which a collection of nodes are linked together by references from one node to the next. To make a linked list, we will define a class of self-referential objects. A self-referential object is an object that contains a reference to an object of the same class. The convention is to name these objects Nodes:
public class Node {
private String name;
private Node next;
}
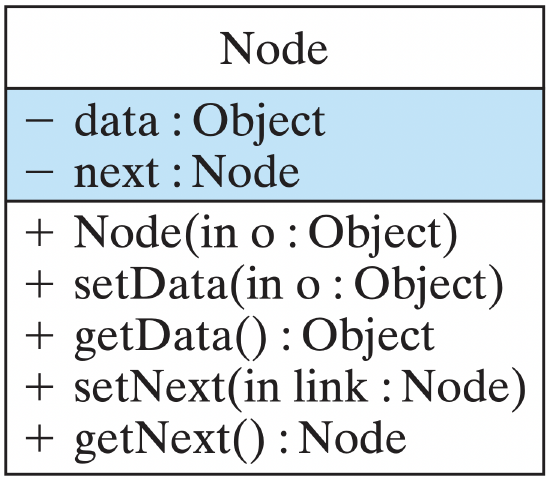
FIGURE 16.2 The Node class.
fig-nodeuml In addition to the reference to a String object, each Node object. The next variable is often called a link because it is used to link together two Node objects. For example, Figure 16.1 provides an illustration of a linked list of Nodes.
By assigning references to the next variables in each Node, we can chain together arbitrarily long lists of objects. Therefore, we will want to add methods to our Node class that enable us to manipulate a Node’s next variable (Fig. 16–2). By assigning it a reference to another Node, we can link two Nodes together. By retrieving the link’s value, we can find the next Node in the list.
JAVA LANGUAGE RULE
Self-Referential Object.
A self-referential object is one that contains an instance variable that refers to an object of the same class.
In addition to the link variable, each Node stores some data. In this example, the data is a single String. But there’s no real limit to the amount and type of data that can be stored in a linked list. Therefore, in addition to methods that manipulate a Node’s link, we will also want methods to manipulate its data. These points suggest the following basic design for a Node:
public class Node {
private Object data;
private Node next;
public Node (Object obj); // Constructor
public void setData (Object obj); // Data access
public Object getData();
public void setNext(Node link); // Link access
public Node getNext();
} // Node
Note that we have defined the Node’s data in the most general possible way: As a reference to an Object. Because the Object class is the root of Java’s entire class hierarchy, an Object can encompass any kind of data. By using Java’s wrapper classes, such as Integer and Double, a Node’s data can even include primitive data.
The important point is that regardless of its type of data, a Node will have data access methods and link access methods. The data access methods differ, depending on the type of data, but the link access methods will generally be the same.
JAVA EFFECTIVE DESIGN
Link Versus Data.
Making a clear distinction between an object’s data and those elements used to manipulate the object is an example of the divide-and-conquer principle.
Exercise 16.1
Write a statement to create a new Node whose data consist of the String “Hello.”
Exercise 16.2
Write a statement to create a new Node whose data consist of the Student named “William.” Assume that the Student class has a constructor with a String parameter for the student’s name.
16.1.2 Example: The Dynamic Phone List
Let’s define a PhoneListNode class that can be used to implement a phone list (Fig. 16.3). This definition will be a straightforward specialization of the generic Node list defined in the previous section. Each element of the phone list will consist of a person’s name and phone number. These will be the node’s data and can be stored in two String variables. To access these data, we will provide a constructor and a basic set of access methods. Thus, we have the definition shown in Figure 16.4.

Figure 16.3: Design of the PhoneListNode class.

Figure 16.4: The PhoneListNode class.
The constructor and data access methods should be familiar to you. Note that the constructor sets the initial value of next to null, which means that it refers to no object.
JAVA DEBUGGING TIP
Null Reference.
A common programming error is the attempt to use a null reference to refer to an object. This usually means the reference has not been successfully initialized.
Manipulating a list’s nodes
Let’s discuss the details of the link access methods—the setNext() and getNext() methods—which are also simple to implement. Because this is a PhoneListNode, these methods take PhoneListNode as a parameter and return type, respectively. Given a reference to a PhoneListNode, the setNext() method assigns it to next. The getNext() method simply returns the value of its next link.
Let’s now see how we would use these methods to construct a list. The following statements create three nodes:

Figure 16.5: The phone list: a linked list of nodes, each of which contains a person’s name and phone number.
PhoneListNode node1 =
new PhoneListNode ( ”Roger M” , ”090−997−2918” ) ;
PhoneListNode node2 =
new PhoneListNode ( ” Jane M” , ”090−997−1987” ) ;
PhoneListNode node3 =
new PhoneListNode ( ” Stacy K” , ”090−997−9188” ) ;
The next two statements chain the nodes together into the list shown in Figure 16.5:
node1 . se tNex t ( node2 ) ;
node2 . se tNex t ( node3 ) ;
If we wanted to add a fourth node to the end of this list, we could use the following statements:
PhoneListNode node4 =
new PhoneListNode ( ”gary g” , ”201−119−8765” );
node3 . se tNex t ( node4 ) ;
Although this example illustrates the basic technique for inserting nodes at the end of the list, it depends too much on our knowledge of the list. In order to be truly useful we will have to develop a more general set of methods to create and manipulate a list of nodes. As we will see, a better design would be able to find the end of the list without knowing anything about the list’s data.
JAVA EFFECTIVE DESIGN
Generality
In a well-designed list data structure, you should be able to manipulate its elements without knowing anything about its data.
SELF-STUDY EXERCISE
Exercise 16.3
Suppose you know that nodeptr is a reference to the last element of a linked list of PhoneListNodes. Create a new element for “Bill C” with phone number “111-202-3331” and link it into the end of the list.
16.1.3 Manipulating the Phone List

FIGURE 16.6 The PhoneList class has a reference to the first node of the list (head) and methods to insert, remove, and look up information.
In addition to the Nodes that make a list, we must define a class containing methods to manipulate the list. This class will include the insert, access, and remove methods. It must also contain a reference to the list itself. This leads to the basic design shown in Figure 16.6. Because this is a list of PhoneListNodes, we need a PhoneListNode reference to point to fig-phonelistclass the list, which is the purpose of the head variable.
A preliminary coding of the PhoneList class is shown in Figure 16.7. As you can see there, when a new PhoneList instance is constructed, head is initialized to null, meaning the list is initially empty. Since we will frequently want to test whether the list is empty, we define the boolean isEmpty() method for that purpose. As you can see, its definition says that a list is empty when the reference to the head of this list is null.
JAVA PROGRAMMING TIP
The null Reference.
A null reference is useful for defining limit cases, such as an empty list or an uninstantiated object.

Figure 16.7: A preliminary version of the PhoneList class.
Inserting Nodes into a List
The insert() method will have the task of inserting new PhoneListNodes into the list. There are a number of ways to do this. The node could be inserted at the beginning or at the end of the list, or in alphabetical order, or possibly in other ways. As we’ll see, it is easiest to insert a new node at the head of the list. But for this example, let’s develop a method that inserts the node at the end of the list.
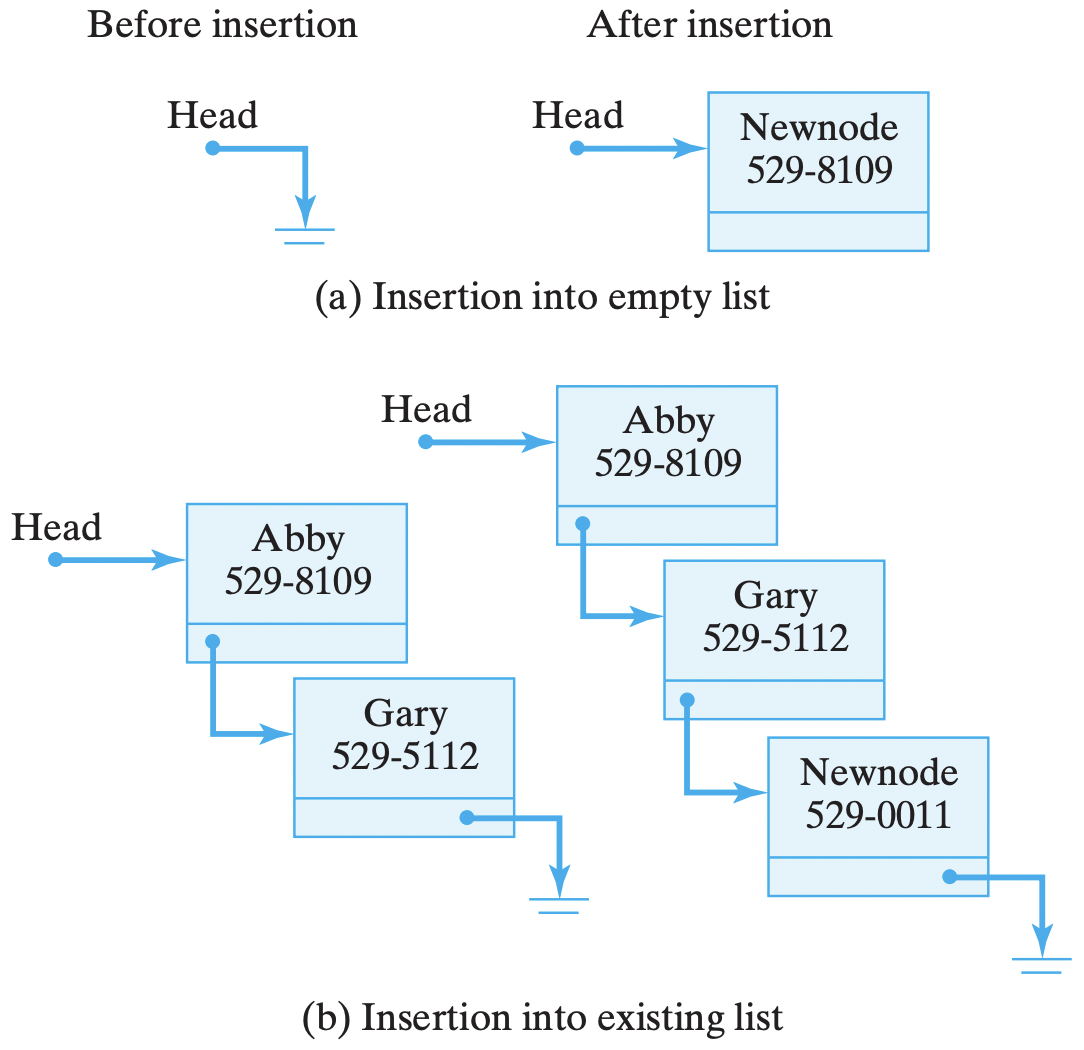
Figure 16.8: Two cases. (a) The list is empty before the insertion, which takes place at head. (b) The list is not empty, so the insertion takes place at the end of the list.
There are two cases we need to worry about for this algorithm. First, if the list is empty, we can insert the node by simply setting head to point to the node [Figure 16.8(a)]. Second, if the list is not empty, we must move through, or traverse, the links of the list until we find the last node and insert the new node after it [Figure 16.8(b)]. In this case, we want to set the next variable of the last node to point to the new node. This gives us the following algorithm:
public void insert ( PhoneListNode newNode ) {
if (isEmpty ( ))
head = newNode; //Insert at head of list
else {
PhoneListNode current = head ; //Start traversal at head
while (current.getNext( )! = null) //While not last node
current = current.getNext( ); //go to next node
current.setNext(newNode); //Do the insertion
}
} //insert( )
Recall that when nodes are linked, their next variables are non-null. So when a node’s next variable is null, that indicates the end of the list—there’s no next node. Thus, our algorithm begins by checking if the list is empty. If so, we assign head the reference to newNode, the PhoneListNode that’s being inserted.
Traversing a list
If the list is not empty, then we need to find the last node. In order to traverse the list, we will need a temporary variable, current, which will always point to the current node. It’s important to understand the while loop used here:
PhoneListNode current = head ; //Initializer
while (current.getNext( ) ! = null) //Entry condition
current = current.getNext( ); // Up dater
Loop-exit condition
The loop variable, current, is initialized by setting it to point to the head of the list. The entry condition tests whether the next link, leading out of current, is null (Fig. 16.9). That is, when the link coming out of a node is null, then that node is the last node in the list [Figure 16.9(c)]. Inside the while loop, the update expression simply assigns the next node to current. In that way, current will point to each successive node until the last node is found. It’s very important that the loop exits when current.getNext() is null—that is, when the next pointer of the current node is null. That way current is pointing to the last node and can be used to set its next variable to the node being inserted [Figure 16.9(d)]. Thus, after the loop is exited, current still points to the last node. At that point, the setNext() method is used to link newNode into the list as the new last node.
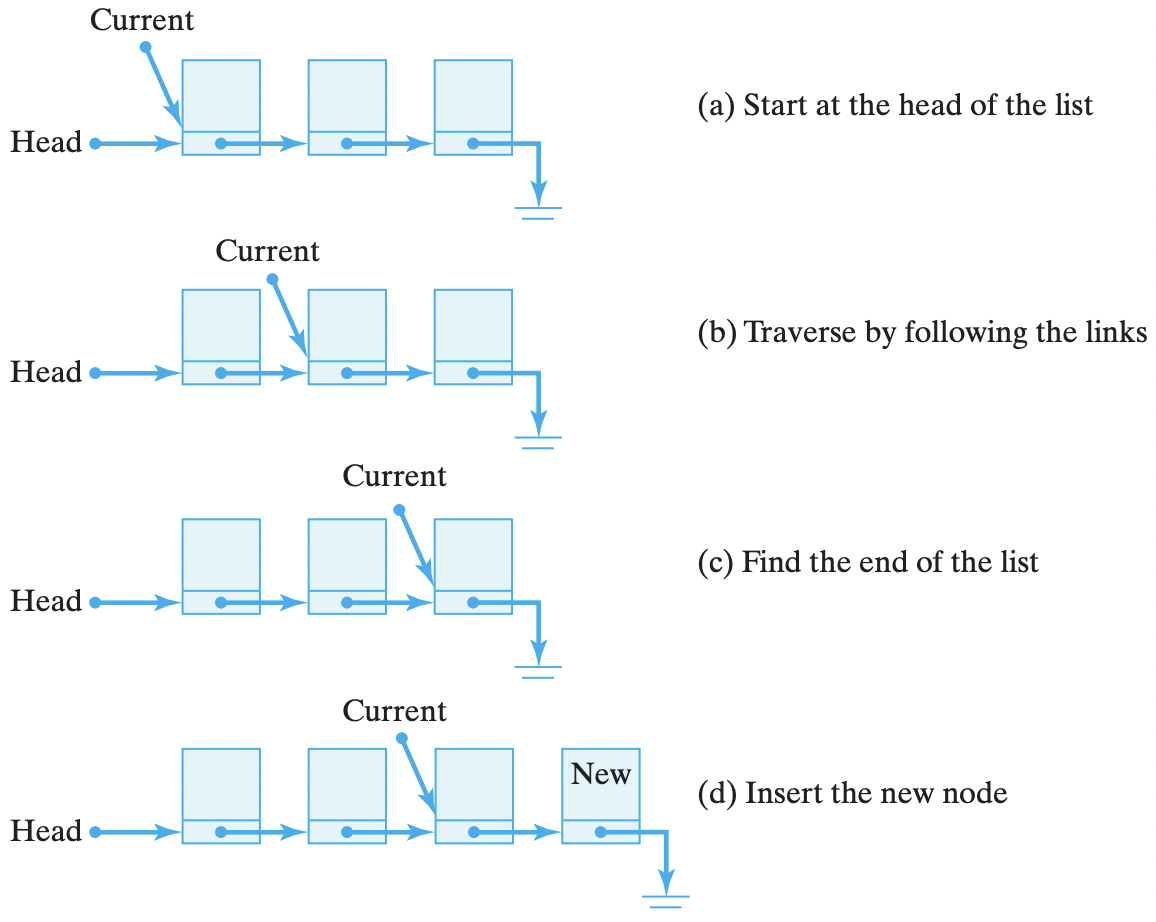
Figure 16.9: The temporary variable current is used to traverse the list to find its end.
JAVA DEBUGGING TIP
List Traversal
A common error in designing list-traversal algorithms is an erroneous loop-entry or loop-exit condition. One way to avoid this error is to hand trace your algorithm to make sure your code is correct.
Printing the Nodes of a List
The print() method also uses a traversal strategy to print the data from each node of the list. Here again it is necessary to test whether the list is empty. If so, we must print an error message. (This would be a good place to throw a programmer-defined exception, such as an EmptyListException.) If the list is not empty, then we use a temporary variable to traverse the list, printing each node’s data along the way:
public void print(){
if (isEmpty())
System.out.println(”Phone list is empty” );
PhoneListNode current = head ; //Start traversal at head
while (current!=null){ //While not end of list
System.out.println(current.toString()); //print data
current=current.getNext(); //go to next node
}
} //print()
Note the differences between this while loop and the one used in the insert() method. In this case, we exit the loop when current becomes null; there’s no action to be taken after the loop is exited. The printing takes place within the loop. Thus, in this case, the entry condition, (current != null), signifies that the task has been completed.
JAVA PROGRAMMING TIP
Terminating a Traversal.
In designing list-traversal algorithms where the reference, \(\ p\), points to the nodes in the list, if you need to refer to the last node in the list after the traversal loop exits, then your exit condition should be p.getNext()==null. If you have finished processing the nodes when the loop exits, your exit condition should be p == null.
Looking up a Node in a List
List traversal
Because the record associated with a person can be located anywhere in List traversal the list, the traversal strategy must also be used to look up someone’s phone number in the PhoneList. Here again we start at the head of the list and traverse through the next links until we find the node containing the desired phone number. This method takes the name of the person as a parameter. There are three cases to worry about: (1) The list is empty; (2) the normal case where the person named is found in the list; and (3) the person named is not in the list. Because the method returns a String, we can return error messages in the first and third cases:
public String getPhone (String name) {
if (isEmpty()) //Case 1 : Empty list
return ”Phone list is empty”;
else {
PhoneListNode current = head;
while ((current.getNext() != null) &&
(!current.getName().equals(name)))
current = current.getNext();
if (current.getName().equals(name))
return current.getData(); //Case2: Found name
else
//Case 3: No such person
return (”Sorry. No entry for” + name);
}
} // getPhone()
Compound exit condition
Note the while loop in this case. As in the insert() method, when the loop exits, we need a reference to the current node so that we can print its phone number [current.getData()]. But here there are three ways to exit the loop: (1) We reach the end of the list without finding the named person; (2) we find the named person in the interior of the list; or (3) we find the named person in the last node of the list. In any case, it is necessary to test whether the name was found or not after the loop is exited. Then appropriate action can be taken.
SELF-STUDY EXERCISE
Exercise 16.4
What if the exit condition for the while loop in getPhone() were stated as
((current.getNext() != null) ||
(!current.getName().equals(name)))
Removing a Node from a List
Node-removal algorithm
By far the most difficult task is that of removing a node from a list. In the PhoneList we use the person’s name to identify the node, and we return a String that can be used to report either success or failure. There are four cases to worry about in designing this algorithm: (1) The list is empty, (2) the first node is being removed, (3) some other node is being removed, and (4) the named person is not in the list. The same traversal strategy we used in getPhone() is used here, with the same basic while loop for cases 3 and 4.
As Figure 16.10 shows, the first two cases are easily handled. If the list is empty, we just return an error message. We use current as the traversal variable. If the named node is the first node, we simply need to set head to current.getNext(), which has the effect of making head point to the second node in the list [Figure 16.11(a)]. Once the node is cut out from the chain of links, there will be no further reference to it. In this case, Java will recapture the memory it uses when it does garbage collection.
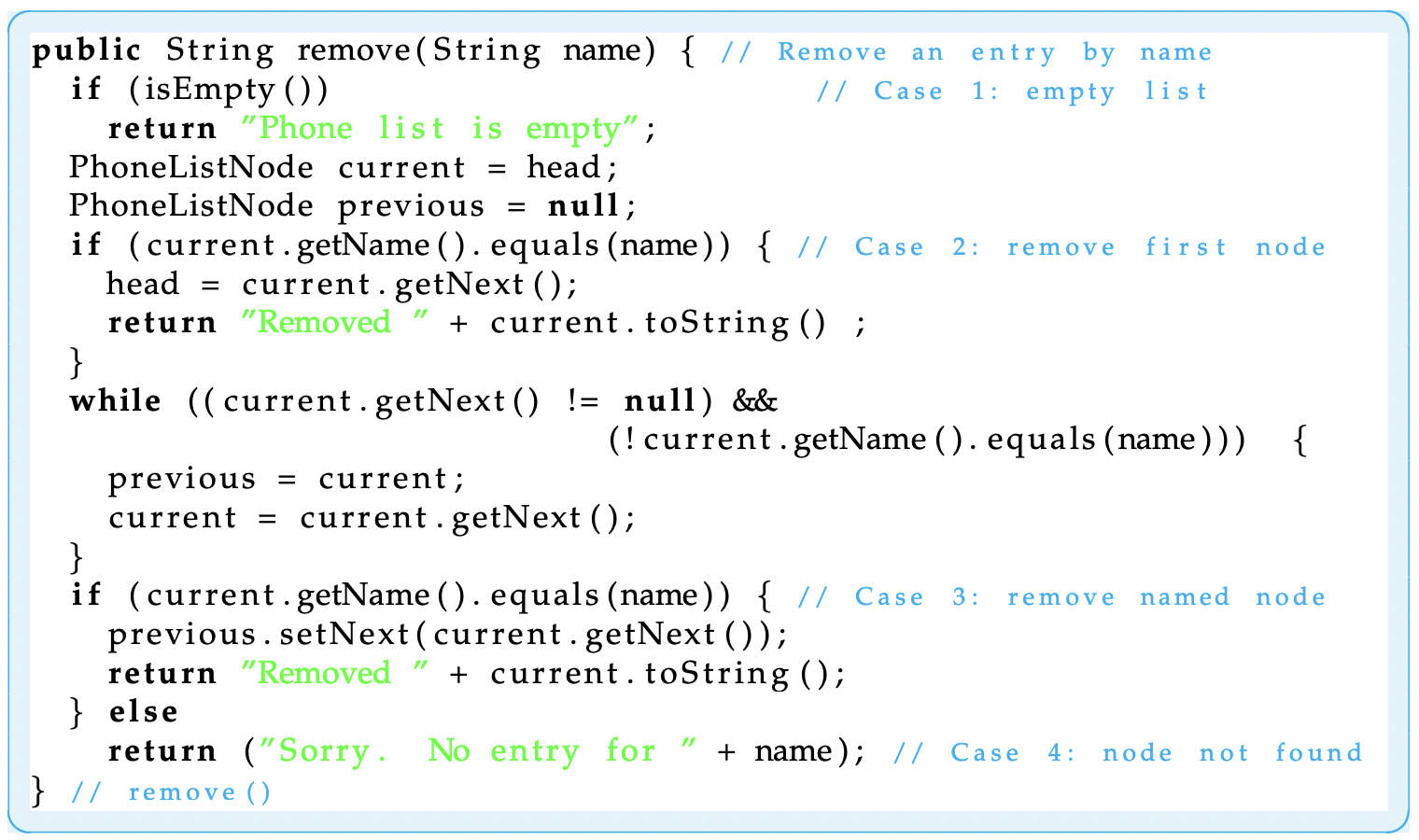
Figure 16.10: The remove() method.
JAVA LANGUAGE RULE
Garbage Collection.
Java’s garbage collector handles the disposal of unused objects automatically. This helps to simplify linked-list applications. In languages such as C++, the programmer would have to dispose of the memory occupied by the deleted node.
Tandem traversal
In order to remove some other node besides the first, two traversal variables are needed: previous and current. They proceed together down the list, with previous always pointing to the node just before the current node. The reason, of course, is that to remove the current node, you need to adjust the link pointing to it contained in the previous node [Figure 16.11(b)]. That is, the new value of previous.next will be the current value of current.next. We use the getNext() and setNext() methods to effect this change:
previous.setNext(current.getNext());
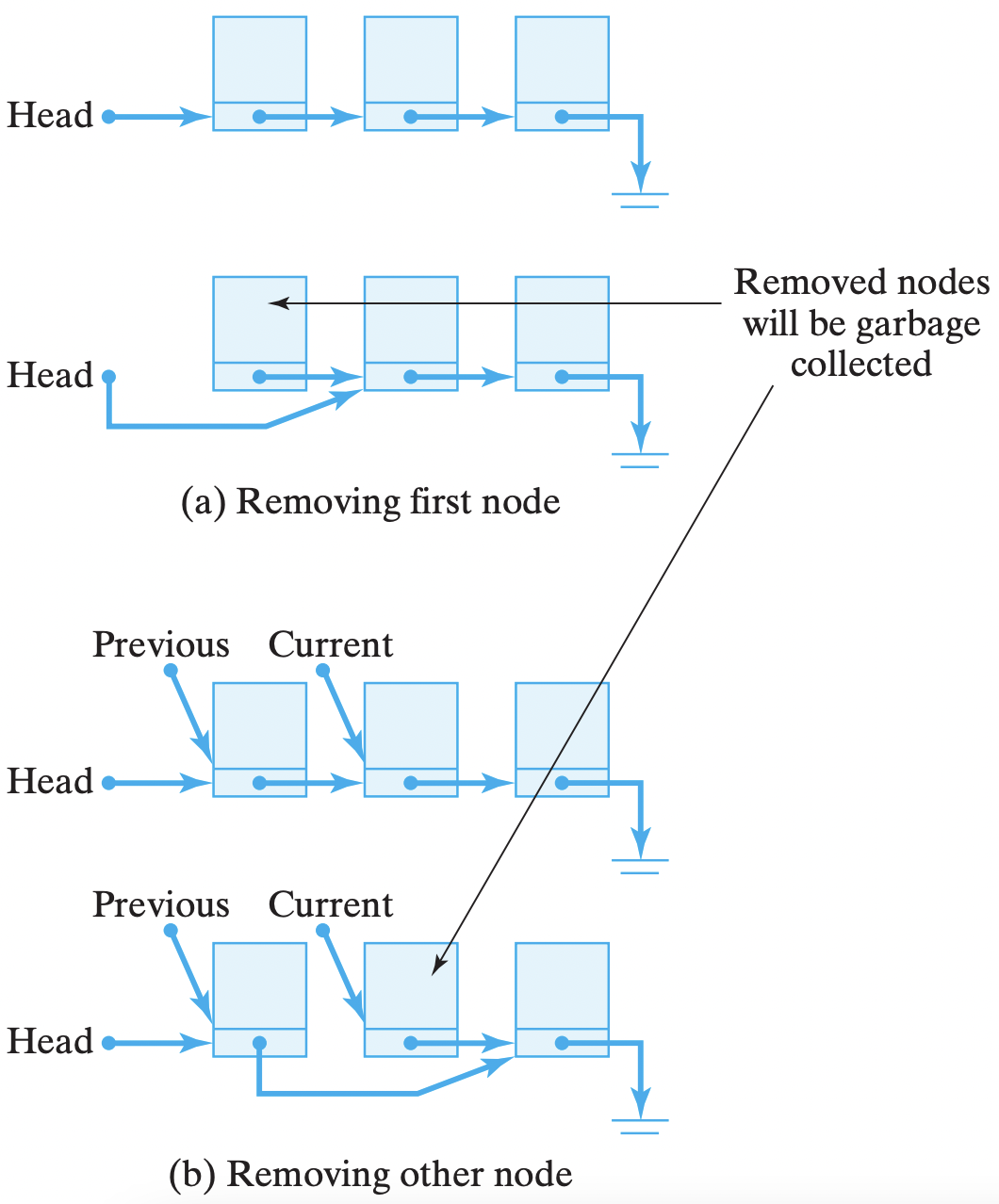 Figure 16.11: Removing different nodes from a linked list.
Figure 16.11: Removing different nodes from a linked list.Testing the List
Designing test data
In developing list-processing programs, it is important to design good test data. As we have seen, both the insertion and removal operations involve several distinct cases. Proper testing of these methods ideally would test every possible case. The main() program in Figure 16.12 illustrates the kinds of tests that should be performed. This method could be incorporated directly into the PhoneList class, or it could be made part of a separate class.
Of course, there are often so many combinations of list operations that exhaustive testing might not be feasible. At the very least you should design test data that test each of the different conditions identified in your algorithms. For example, in testing removals from a list, you should test all four cases that we discussed. In testing insertions or lookups, you should test all three cases that we identified.
JAVA EFFECTIVE DESIGN
Test Data.
Test data for validating list-processing algorithms should (at least) test each of the cases identified in each of the removal and insertion methods.
SELF-STUDY EXERCISES
Exercise 16.5
Trace through the main() method line by line and predict its output.
Exercise 16.6
Design a test of PhoneList that shows that new elements can be inserted into a list after some or all of its previous nodes have been removed.
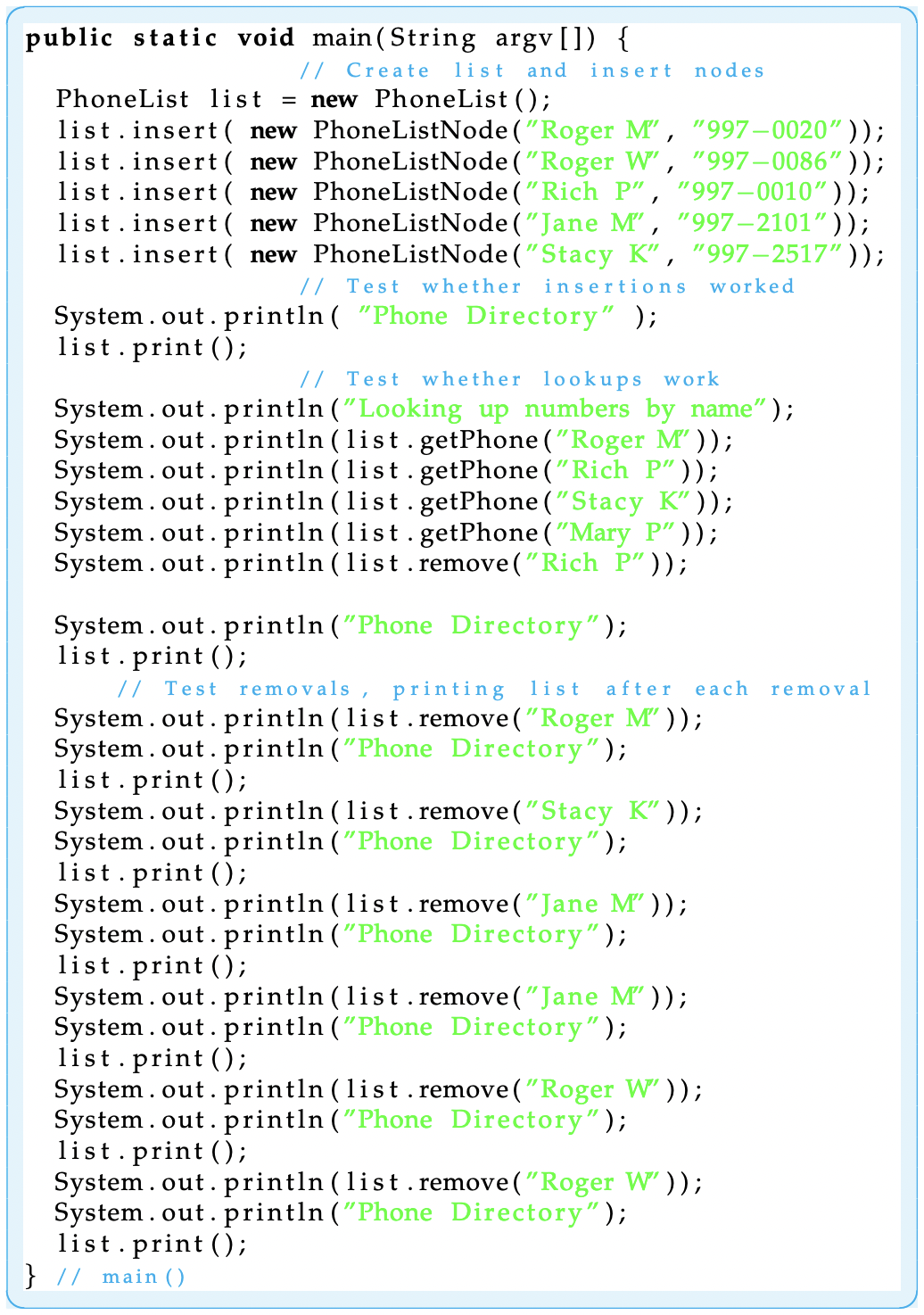
Figure 16.12: A main() method containing a set of tests for the PhoneList class.


