21.4: Hashtables
- Page ID
- 42810
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)To explain how hashtables work and why their performance is so good, I start with a simple implementation of a map and gradually improve it until it’s a hashtable.
I use Python to demonstrate these implementations, but in real life you wouldn’t write code like this in Python; you would just use a dictionary! So for the rest of this chapter, you have to imagine that dictionaries don’t exist and you want to implement a data structure that maps from keys to values. The operations you have to implement are:
- add(k, v):
- Add a new item that maps from key
kto valuev. With a Python dictionary,d, this operation is writtend[k] = v. - get(k):
- Look up and return the value that corresponds to key
k. With a Python dictionary,d, this operation is writtend[k]ord.get(k).
For now, I assume that each key only appears once. The simplest implementation of this interface uses a list of tuples, where each tuple is a key-value pair.
class LinearMap:
def __init__(self):
self.items = []
def add(self, k, v):
self.items.append((k, v))
def get(self, k):
for key, val in self.items:
if key == k:
return val
raise KeyError
add appends a key-value tuple to the list of items, which takes constant time.
get uses a for loop to search the list: if it finds the target key it returns the corresponding value; otherwise it raises a KeyError. So get is linear.
An alternative is to keep the list sorted by key. Then get could use a bisection search, which is \( O(\log{n}) \). But inserting a new item in the middle of a list is linear, so this might not be the best option. There are other data structures that can implement add and get in log time, but that’s still not as good as constant time, so let’s move on.
One way to improve LinearMap is to break the list of key-value pairs into smaller lists. Here’s an implementation called BetterMap, which is a list of 100 LinearMaps. As we’ll see in a second, the order of growth for get is still linear, but BetterMap is a step on the path toward hashtables:
class BetterMap:
def __init__(self, n=100):
self.maps = []
for i in range(n):
self.maps.append(LinearMap())
def find_map(self, k):
index = hash(k) % len(self.maps)
return self.maps[index]
def add(self, k, v):
m = self.find_map(k)
m.add(k, v)
def get(self, k):
m = self.find_map(k)
return m.get(k)
__init__ makes a list of \( n \) LinearMaps.
find_map is used by add and get to figure out which map to put the new item in, or which map to search.
find_map uses the built-in function hash, which takes almost any Python object and returns an integer. A limitation of this implementation is that it only works with hashable keys. Mutable types like lists and dictionaries are unhashable.
Hashable objects that are considered equivalent return the same hash value, but the converse is not necessarily true: two objects with different values can return the same hash value.
find_map uses the modulus operator to wrap the hash values into the range from 0 to len(self.maps), so the result is a legal index into the list. Of course, this means that many different hash values will wrap onto the same index. But if the hash function spreads things out pretty evenly (which is what hash functions are designed to do), then we expect \( n/100 \) items per LinearMap.
Since the run time of LinearMap.get is proportional to the number of items, we expect BetterMap to be about 100 times faster than LinearMap. The order of growth is still linear, but the leading coefficient is smaller. That’s nice, but still not as good as a hashtable.
Here (finally) is the crucial idea that makes hashtables fast: if you can keep the maximum length of the LinearMaps bounded, LinearMap.get is constant time. All you have to do is keep track of the number of items and when the number of items per LinearMap exceeds a threshold, resize the hashtable by adding more LinearMaps.
Here is an implementation of a hashtable:
class HashMap:
def __init__(self):
self.maps = BetterMap(2)
self.num = 0
def get(self, k):
return self.maps.get(k)
def add(self, k, v):
if self.num == len(self.maps.maps):
self.resize()
self.maps.add(k, v)
self.num += 1
def resize(self):
new_maps = BetterMap(self.num * 2)
for m in self.maps.maps:
for k, v in m.items:
new_maps.add(k, v)
self.maps = new_maps
__init__ creates a BetterMap and initializes num, which keeps track of the number of items.
get just dispatches to BetterMap. The real work happens in add, which checks the number of items and the size of the BetterMap: if they are equal, the average number of items per LinearMap is 1, so it calls resize.
resize make a new BetterMap, twice as big as the previous one, and then “rehashes” the items from the old map to the new.
Rehashing is necessary because changing the number of LinearMaps changes the denominator of the modulus operator in find_map. That means that some objects that used to hash into the same LinearMap will get split up (which is what we wanted, right?).
Rehashing is linear, so resize is linear, which might seem bad, since I promised that add would be constant time. But remember that we don’t have to resize every time, so add is usually constant time and only occasionally linear. The total amount of work to run add \( n \) times is proportional to \( n \), so the average time of each add is constant time!
To see how this works, think about starting with an empty HashTable and adding a sequence of items. We start with 2 LinearMaps, so the first 2 adds are fast (no resizing required). Let’s say that they take one unit of work each. The next add requires a resize, so we have to rehash the first two items (let’s call that 2 more units of work) and then add the third item (one more unit). Adding the next item costs 1 unit, so the total so far is 6 units of work for 4 items.
The next add costs 5 units, but the next three are only one unit each, so the total is 14 units for the first 8 adds.
The next add costs 9 units, but then we can add 7 more before the next resize, so the total is 30 units for the first 16 adds.
After 32 adds, the total cost is 62 units, and I hope you are starting to see a pattern. After \( n \) adds, where \( n \) is a power of two, the total cost is \( 2n-2 \) units, so the average work per add is a little less than 2 units. When \( n \) is a power of two, that’s the best case; for other values of \( n \) the average work is a little higher, but that’s not important. The important thing is that it is \( O(1) \).
Figure \(\PageIndex{1}\) shows how this works graphically. Each block represents a unit of work. The columns show the total work for each add in order from left to right: the first two adds cost 1 unit each, the third costs 3 units, etc.
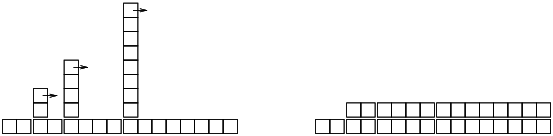
The extra work of rehashing appears as a sequence of increasingly tall towers with increasing space between them. Now if you knock over the towers, spreading the cost of resizing over all adds, you can see graphically that the total cost after \( n \) adds is \( 2n - 2 \).
An important feature of this algorithm is that when we resize the HashTable it grows geometrically; that is, we multiply the size by a constant. If you increase the size arithmetically—adding a fixed number each time—the average time per add is linear.
You can download my implementation of HashMap from http://thinkpython2.com/code/Map.py, but remember that there is no reason to use it; if you want a map, just use a Python dictionary.


