6.3: Exercises
- Page ID
- 6431
Exercise \(\PageIndex{1}\)
List the main high-level tasks in a ‘waterfall’ ontology development methodology.
Exercise \(\PageIndex{2}\)
Explain the difference between macro and micro level development.
Exercise \(\PageIndex{3}\)
What is meant by ‘encoding peculiarities’ of an ontology?
Exercise \(\PageIndex{4}\)
Methods were grouped into four categories. Name them and describe their differences.
Exercise \(\PageIndex{5}\)
Give two examples of types of modelling flaws, i.e., that are possible causes of undesirable deductions.
Exercise \(\PageIndex{6}\)
Ontology development methodologies have evolved over the past 20 years. Compare the older Methontology with the newer NeON methodology.
Exercise \(\PageIndex{7}\)
Consider the following CQs and evaluate the AfricanWildlifeOntology1.owl against them. If these were the requirements for the content, is it a ‘good’ ontology?
- Which animal eats which other animal?
- Is a rockdassie a herbivore?
- Which plant parts does a giraffe eat?
- Does a lion eat plants or plant parts?
- Is there an animal that does not drink water?
- Which plants eat animals?
- Which animals eat impalas?
- Which animal(s) is(are) the predators of rockdassies?
- Are there monkeys in South Africa?
- Which country do I have to visit to see elephants?
- Do giraffes and zebras live in the same habitat?
- Answer
-
No, in that case, it is definitely not a good ontology. First, there are several CQs for which the ontology does not have an answer, such as not having any knowledge of monkeys represented. Second, it does contain knowledge that is not mentioned in any of the CQs, such as the carnivorous plant.
Exercise \(\PageIndex{8}\)
Carry out at least subquestion a) and if you have started with, or already completed, the practical assignment at the end of Block I, do also subquestion b).
a. Take the Pizza ontology pizza.owl, and submit it to the OOPS! portal. Based on its output, what would you change in the ontology, if anything?
b. Submit your ontology to OOPS! How does it fare? Do you agree with the critical/non-critical categorisation by OOPS!? Would you change anything based on the output, i.e.: does it assist you in the development of your ontology toward a better quality ontology?
- Answer
-
Note \(\PageIndex{1}\)
Double-checking this answer, it turns out there are various versions of the pizza ontology. The answer given here is based on the output from the version I submitted in 2015; the output is available as “OOPS! - OntOlogy Pitfall Scanner! - Results pizza.pdf” in the PizzaOOPS.zip file from the book’s website. The other two are: “OOPS! - OntOlogy Pitfall Scanner! - ResultsPizzaLocal.pdf” based on pizza.owl from Oct 2005 that was distributed with an old Prot´eg´e version and “OOPS! - OntOlogy Pitfall Scanner! - ResultsPizzaProtegeSite.pdf”, who’s output is based on having given OOPS! the URI protege.stanford.edu/ontolog...izza/pizza.owl in July 2018.
There are 39 pitfalls detected and categorised as ‘minor’, and 4 as ‘important’. (explore the other pitfalls to see which ones are minor, important, and critical).
The three “unconnected ontology elements” are used as a way to group things, so are not really unconnected, so that can stay.
ThinAndCripsyBaseis detected as a “Merging different concepts in the same class” pitfall. Aside from the typo, one has to inspect the ontology to determine whether it can do with an improvement: what are its sibling, parent and child classes, what is its annotation? It is disjoint withDeepPanBase, but there is no other knowledge. It could just as well have been namedThinBase, but the original class was likely not intended as a real merging of classes, at least not like a class called, say,UndergradsAndPostgrads.Then there are 31 missing annotations. Descriptions can be added to say what a
DeepPanBaseis, but for the toppings this seems less obvious to add.The four object properties missing domain and range axioms was a choice by the modellers (see the tutorial) to not ‘overcomplicate’ the tutorial for novice modellers as they can have ‘surprising’ deductions, but it would be better to add them where possible.
Last, OOPS detected that the same four properties are missing inverses. This certainly can be added for
isIngredientOfandhasIngredient. That said, in OWL 2, one also can usehasIngredient−to stand in for the notion of “isIngredientOf”, so missing inverses is not necessarily a problem. (Ontologically, one easily could argue for ’non-directionality’, but that is a separate line of debate; see e.g., [Fin00, KC16]).
Exercise \(\PageIndex{9}\)
There is some ontology \(O\) that contains the following expressions:
\(\texttt{R}\sqsubseteq\texttt{PD}\times\texttt{PD}\), \(\texttt{PD}\sqsubseteq\texttt{PT}\), \(\texttt{A}\sqsubseteq\texttt{ED}\), \(\texttt{A}\sqsubseteq\exists\texttt{R.B}\),
\(\texttt{S}\sqsubseteq\texttt{PT}\times\texttt{PT}\), \(\texttt{ED}\sqsubseteq\texttt{PT}\), \(\texttt{B}\sqsubseteq\texttt{ED}\), \(\texttt{D}\sqsubseteq\exists\texttt{S.C}\).
\(\texttt{S}\sqsubseteq\texttt{R}\), \(\texttt{ED}\sqsubseteq\neg\texttt{PD}\), \(\texttt{C}\sqsubseteq\texttt{PD}\),
\(\texttt{Trans(R)}\), \(\texttt{D}\sqsubseteq\texttt{PD}\),
Answer the following questions:
a. Is \(\texttt{A}\) consistent? Verify this with the reasoner and explain why.
b. What would the output be when applying the RBox Compatibility service? Is the knowledge represented ontologically flawed?
- Answer
-
No, \(\texttt{A}\) is unsatisfiable. Reason: \(\texttt{A}\sqsubseteq\texttt{ED}\) (EnDurant), it has a property \(\texttt{R}\) (to \(\texttt{B}\)), which has declared as domain \(\texttt{PD}\) (PerDurant), but \(\texttt{ED}\sqsubseteq\neg\texttt{PD}\) (endurant and perdurant are disjoint), hence, \(\texttt{A}\) cannot have any instances.
Exercise \(\PageIndex{10}\)
Apply the OntoClean rules to the flawed ontology depicted in Figure 5.3.1, i.e., try to arrive at a ‘cleaned up’ version of the taxonomy by using the rules. The other properties are, in short:
- Identity: being able to recognise individual entities in the world as being the same (or different); Any property carrying an IC: \(+\)I (\(-\) I otherwise); Any property supplying an IC: \(+\)O (\(-\)O otherwise) (“O” is a mnemonic for “own identity”); \(+\)O implies \(+\)I and \(+\)R.
- Unity: being able to recognise all the parts that form an individual entity; e.g., ocean carries unity (\(+\)U), legal agent carries no unity (\(-\)U), and amount of water carries anti-unity (“not necessarily wholes”, ∼U)
- Identity criteria are the criteria we use to answer questions like, “is that my dog?”
- Identity criteria are conditions used to determine equality (sufficient conditions) and that are entailed by equality (necessary conditions)
With the rules:
- Given two properties, \(p\) and q, when \(q\) subsumes \(p\) the following constraints hold:
– If \(q\) is anti-rigid, then \(p\) must be anti-rigid
– If \(q\) carries an IC, then \(p\) must carry the same IC
– If \(q\) carries a UC, then \(p\) must carry the same UC
– If \(q\) has anti-unity, then \(p\) must also have anti-unity
- Incompatible IC’s are disjoint, and Incompatible UC’s are disjoint
- And, in shorthand:
– \(+R\not\subset ~R\)
– \(−I\not\subset +I\)
– \(−U\not\subset +U\)
– \(+U\not\subset ∼ U\)
– \(−D\not\subset +D\)
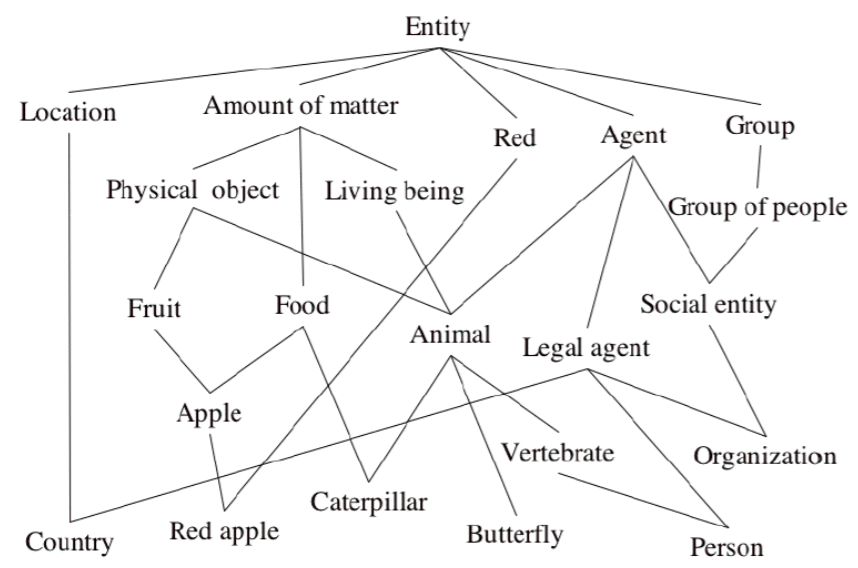.png?revision=1)
Figure 5.4.1: An ‘unclean’ taxonomy. (Source: OntoClean teaching material by Guarino)
- Answer
-
There are several slides with the same ‘cleaning procedure’ and one of them is uploaded on the book’s webpage, which was from the Doctorate course on Formal Ontology for Knowledge Representation and Natural Language Processing 2004-2005, slide deck “Lesson3-OntoClean”. Meanwhile, there is also a related paper that describes the steps in more detail, which appeared in the Handbook on Ontologies [GW09].
Exercise \(\PageIndex{11}\)
Pick a topic—such as pets, buildings, government—and step through one of the methodologies to create an ontology. The point here is to try to apply a methodology, not to develop an ontology, so even one or two CQs and one or two axioms in the ontology will do.


