3.2.2: Link between logic and set theory
- Page ID
- 10722
Just as the laws of logic allow us to do algebra with logical formulas, the laws of set theory allow us to do algebra with sets. Because of the close relationship between logic and set theory, their algebras are very similar. The algebra of sets, like the algebra of logic, is Boolean algebra. When George Boole wrote his 1854 book about logic, it was really as much about set theory as logic. In fact, Boole did not make a clear distinction between a predicate and the set of objects for which that predicate is true. His algebraic laws and formulas apply equally to both cases. More exactly, if we consider only subsets of some given universal set U, then there is a direct correspondence between the basic symbols and operations of propositional logic and certain symbols and operations in set theory, as shown in this table:
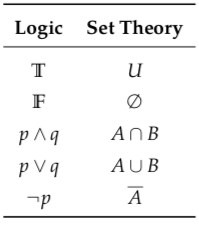
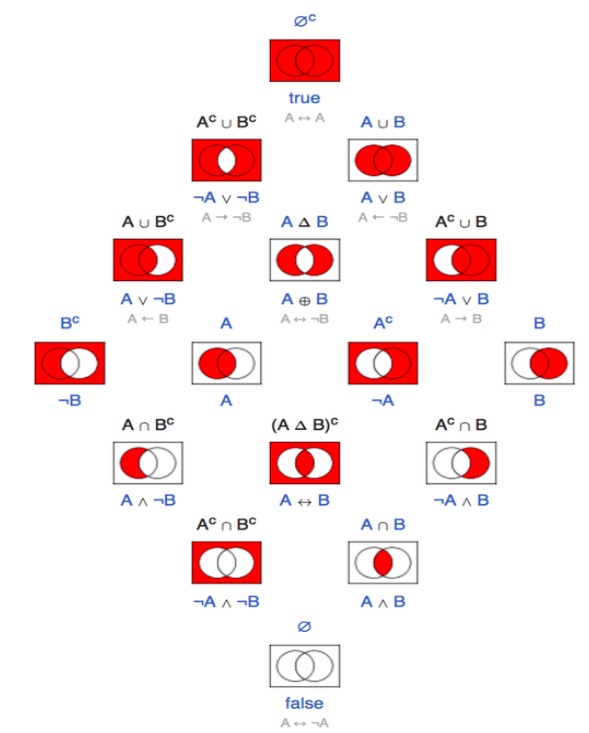
Figure 4.5: The correspondence between set operators and propositional operators. Source: commons.wikimedia.org/wiki/Template:Operations_and_ relations_in_set_theory_and_logic
Any valid logical formula or computation involving propositional variables and the symbols T, F, ∧, ∨, and ¬ can be transformed into a valid formula or computation in set theory by replacing the propositions in the formula with subsets of U and replacing the logical symbols with U, ∅, ∩, ∪, and the complement operator. Figure 4.5 illustrates.
Just as in logic, the operations of set theory can be combined to form complex expressions such as \((A \cup C) \cap(B \cup \overline{C} \cup D) .\) Parentheses can always be used in such expressions to specify the order in which the operations are to be performed. In the absence of paren- theses, we need precedence rules to determine the order of operation. The precedence rules for the Boolean algebra of sets are carried over directly from the Boolean algebra of propositions. When union and intersection are used together without parentheses, in- tersection has precedence over union. Furthermore, when several operators of the same type are used without parentheses, then they are evaluated in order from left to right. (Of course, since ∪ and ∩ are both associative operations, it really doesn’t matter whether the order of evaluation is left-to-right or right-to-left.) For example, A ∪ B ∩ C ∪ D is evaluated as (A ∪ (B ∩ C)) ∪ D. The complement operation is a special case. Since it is denoted by drawing a line over its operand, there is never any ambiguity about which part of a formula it applies to.
Unfortunately in hand-written work this is not always true. Make sure to write neatly and unambiguously when working with complements. Also note that, similarly to parentheses in propositional logic, although paren- theses may not be necessary we strongly encourage you to add them them to improve readability of the order of operations.
The laws of set theory can be used to simplify complex expressions involving sets. (As usual, of course, the meaning of ‘simplification’ is partly in the eye of the beholder.) For example, for any sets X and Y,
\((X \cup Y) \cap(Y \cup X)=(X \cup Y) \cap(X \cup Y) \quad\) (Commutative Law)
\(=(X \cup Y) \quad\) (Idempotent Law)
where in the second step, the Idempotent Law, which says that A ∩ A = A, is applied with A = X ∪ Y. For expressions that use the complement operation, it is usually considered to be simpler to apply the operation to an individual set, as in \(\overline{A},\) rather than to a formula, as in \(\overline{A \cap B} .\) DeMorgan's Laws can always be used to simplify an expression in which the complement operation is applied to a formula. For example,
\(A \cap \overline{B \cup \overline{A}}=A \cap(\overline{B} \cap \overline{A}) \quad\) (DeMorgan's Law)
\(=A \cap(\overline{B} \cap A) \quad\) (Double Complement)
\(=A \cap(A \cap \overline{B}) \quad\) (Commutative Law)
\(=(A \cap A) \cap \overline{B} ) \quad\) (Associative Law)
\(=A \cap \overline{B} \quad\) (Idempotent Law)
As a final example of the relationship between set theory and logic, consider the set-theoretical expression A ∩ (A ∪ B) and the corresponding compound proposition \(p \wedge(p \vee q) .\) (These correspond since for any \(x, x \in A \cap(A \cup B) \equiv(x \in A) \wedge((x \in\) A) \(\vee(x \in B) ) . )\) You might find it intuitively clear that \(A \cap(A \cup B)=A .\) Formally, this follows from the fact that p ∧ (p ∨ q) ≡ p, which might be less intuitively clear and is surprising difficult to prove algebraically from the laws of logic. However, there is another way to check that a logical equivalence is valid: Make a truth table. Consider a truth table for p ∧ (p ∨ q):
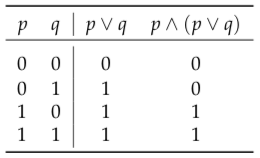
The fact that the first column and the last column of this table are identical shows that \(p \wedge(p \vee q) \equiv p .\) Taking \(p\) to be the proposition \(x \in A\) and \(q\) to be the proposition \(x \in B,\) it follows that the sets A and A ∩ (A ∪ B) have the same members and therefore are equal.
In one of the pencasts of the course, we describe how Venn diagrams can also be used as alternatives to truth tables based on an old exam question. You can find that pencast here: youtu.be/5xle5qfrh0k.
Exercises
- Use the laws of logic to verify the associative laws for union and intersection. That is, show
that if A, B, and C are sets, then A ∪ (B ∪ C) = (A ∪ B) ∪ C and A ∩ (B ∩ C) = (A ∩ B) ∩ C.
- Show that for any sets A and B, A ⊆ A ∪ B and A ∩ B ⊆ A.
- Recall that the symbol ⊕ denotes the logical exclusive or operation. If A and B sets, define the set A △ B by A △ B = {x | (x ∈ A) ⊕ (x ∈ B)}. Show that A △ B = (A ∖ B) ∪ (B ∖ A). (A △ B is known as the symmetric difference of A and B.)
- Choose three non-empty sets A, B, C. Draw a Venn diagram of A △ B △ C.
- Let \(A\) be a subset of some given universal set \(U .\) Verify that \(\overline{\overline{A}}=A\) and that \(A \cup \overline{A}=U\)
- Verify the second of DeMorgan's Laws for sets, \(\overline{A \cap B}=\overline{A} \cup \overline{B} .\) For each step in your verification, state why that step is valid.
- The subset operator, ⊆, is defined in terms of the logical implication operator, →. However, ⊆differs from the ∩ and ∪ operators in that A ∩ B and A ∪ B are sets, while A ⊆ B is a statement. So the relationship between ⊆ and → isn’t quite the same as the relationship between ∪ and ∨or between ∩ and ∧. Nevertheless, ⊆ and → do share some similar properties. This problem shows one example.
- Show that the following three compound propositions are logically equivalent: p → q,(p ∧ q) ↔ p, and (p ∨ q) ↔ q.
- Show that for any sets A and B, the following three statements are equivalent: A ⊆ B,A ∩ B = A, and A ∪ B = B.
- DeMorgan’s Laws apply to subsets of some given universal set U. Show that for a subset X of U,\(\overline{X}\) = U∖X. It follows that DeMorgan’s Laws can be written as U∖(A∪B) = (U∖A)∩(U∖B) and U ∖ (A ∩ B) = (U ∖ A) ∪ (U ∖ B). Show that these laws hold whether or not A and Bare subsets of U. That is, show that for any sets A, B, and C, C ∖ (A ∪ B) = (C ∖ A) ∩ (C ∖ B)and C ∖ (A ∩ B) = (C ∖ A) ∪ (C ∖ B).
- Show that A ∪ (A ∩ B) = A for any sets A and B.
- Let X and Y be sets. Simplify each of the following expressions. Justify each step in the simplification with one of the rules of set theory.
- a. X ∪ (Y ∪ X) b. \((X \cap Y) \cap \overline{X}\)
- c. \((X \cup Y) \cap \overline{Y}\) d. (X ∪ Y) ∪ (X ∩ Y)
- Let A, B, and C be sets. Simplify each of the following expressions. In your answer, the com- plement operator should only be applied to the individual sets A, B, and C
- a. \(\overline{A \cup B \cup C}\) b. \(\overline{A \cup B \cap C}\) c. \(\overline{\overline{A \cup B}}\) d. \(\overline{B \cap \overline{C}}\) e. \(\overline{A \cap \overline{B \cap \overline{C}}}\) f. \(A \cap \overline{A \cup B}\)
- Use induction to prove the following generalized DeMorgan’s Law for set theory: For any natural number \(n \geq 2\) and for any sets \(X_{1}, X_{2}, \ldots, X_{n}\), \(\overline{X_{1} \cap X_{2} \cap \cdots \cap X_{n}}=\overline{X_{1}} \cup \overline{X_{2}} \cup \cdots \cup \overline{X_{n}}\)
- State and prove generalized distributive laws for set theory.

