2.2: The Boolean Algebra of Sets
- Page ID
- 6716
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is clear that set theory is closely related to logic. The intersection and union of sets can be defined in terms of the logical “and” and logical “or” operators. The notation \(\{x|P(x)\}\) makes it possible to use predicates to specify sets. And if \(A\) is any set, then the formula \(x ∈ A\) defines a one place predicate that is true for an entity \(x\) if and only if \(x\) is a member of \(A\). So it should not be a surprise that many of the rules of logic have analogs in set theory.
For example, we have already noted that \(\cup\) and \(\cap\) are commutative operations. This fact can be verified using the rules of logic. Let \(A\) and \(B\) be sets. According to the definition of equality of sets, we can show that \(A \cup B=B \cup A\) by showing that \(∀x((x∈A∪B)↔(x∈B∪A))\). But for any \(x\),
\[ \begin{align*} x \in A \cup B &↔ x \in A \lor x \in B \text{ (definition of ∪)} \\[4pt]& ↔ x \in B \lor x \in A \text{ (commutativity of ∨) } \\[4pt]&↔ x \in B \cup A \text{ (definition of ∪)} \end{align*}\]
The commutativity of ∩ follows in the same way from the definition of ∩ in terms of ∧ and the commutativity of ∧, and a similar argument shows that union and intersection are associative operations.
The distributive laws for propositional logic give rise to two similar rules in set theory. Let \(A, B,\) and \(C\) be any sets. Then
\[A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) \nonumber\]
and
\[A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) \nonumber\]
These rules are called the distributive laws for set theory. To verify the first of these laws, we just have to note that for any \(x\),
\[ \begin{align*} x ∈ A ∪ (B ∩ C) &↔ (x ∈ A) ∨ ((x ∈ B) ∧ (x ∈ C)) \text{ (definition of ∪, ∩) } \\[4pt]& ↔((x∈A)∨(x∈B))∧((x∈A)∨(x∈C)) \text{ (distributivity of ∨) } \\[4pt]&↔ (x ∈ A ∪ B) ∧ (x ∈ A ∪ C) \text{ (definition of ∪) } \\[4pt]&↔ x ∈ ((A ∪ B) ∩ (A ∪ C)) \text{ (definition of ∩) } \end{align*}\]
The second distributive law for sets follows in exactly the same way.
While \(\cup\) is analogous to ∨ and \(cap\) is analogous to ∧, we have not yet seen any operation is set theory that is analogous to the logical “not” operator, \(\neg\). Given a set \(A\), it is tempting to try to define \({x | ¬(x ∈ A)}\), the set that contains everything that does not belong to \(A\). Unfortunately, the rules of set theory do not allow us to define such a set. The notation \({x | P (x)}\) can only be used when the domain of discourse of \(P\) is a set, so there must be an underlying set from which the elements that are/are not in \(A\) are chosen, i.e. some underlying set of which \(A\) is a subset. We can get around this problem by restricting the discussion to subsets of some fixed set. This set will be known as the universal set. Keep in mind that the universal set is only universal for some particular discussion. It is simply some set that is large enough to contain all the sets under discussion as subsets. Given a universal set \(U\) and any subset \(A\) of \(U\), we can define the set \(\{x ∈ U | ¬(x ∈ A)\}\).
Definition 2.1: complement
Let \(U\) be a given universal set, and let \(A\) be any subset of \(U\). We define the complement of \(A\) in \(U\) to be the set \(A\) that is defined by \(\complement{A} = \{x ∈ U | x \notin A\}.\)
Usually, we will refer to the complement of \(A\) in \(U\) simply as the complement of \(A\), but you should remember that whenever complements of sets are used, there must be some universal set in the background.
Given the complement operation on sets, we can look for analogs to the rules of logic that involve negation. For example, we know that \(p ∧ ¬p = \mathbb{F}\) for any proposition \(p\). It follows that for any subset \(A \) of \(U\),
\[\begin{align*} A \cap \complement{A} &= \{x \in U | (x \in A) \land (x \in \complement(A)\} \text{ (definition of ∩) } \\[4pt]&= \{x \in U | ( \in A) \land (x \notin A)\} \text{ (definition of complement) } \\[4pt]&= \{x \in U | (x \in A) \land \neg(x \in A)\} \text{ (definition of } \notin \text{ ) } )\\[4pt]&= \emptyset \end{align*}\]
the last equality following because the proposition \((x ∈ A) ∧ ¬(x ∈ A)\) is false for any \(x\). Similarly, we can show that \(A∪ \bar{A} = U\) and that \(\bar{\bar{A}} =A\) (where \(\bar{\bar{A}}\) is the complement of the complement of \(A\), that is, the set obtained by taking the complement of \(\bar{A}\).)
The most important laws for working with complements of sets are DeMorgan’s Laws for sets. These laws, which follow directly from DeMorgan’s Laws for logic, state that for any subsets \(A\) and \(B\) of a universal set \(U\),
\[\bar{A∪B} = \bar{A} \cap \bar{B} \nonumber \]
and
\[\bar{A∩B} = \bar{A} \cup \bar{B} \nonumber\]
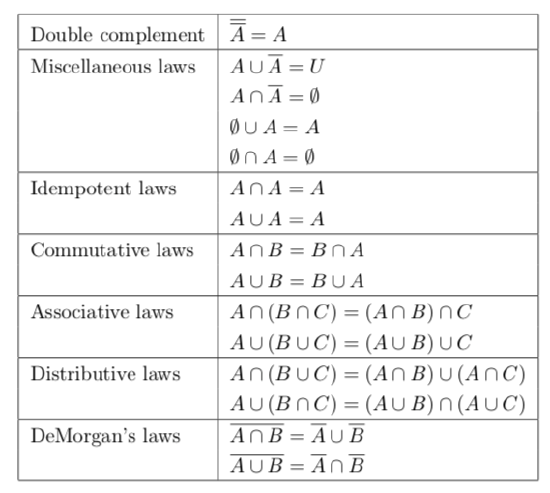
Figure 2.2: Some Laws of Boolean Algebra for sets. \(A, B,\) and \(C\) are sets. For the laws that involve the complement operator, they are assumed to be subsets of some universal set, \(U\). For the most part, these laws correspond directly to laws of Boolean Algebra for propositional logic as given in Figure 1.2.
For example, we can verify the first of these laws with the calculation
\[ \begin{align*} \overline{A \cup B} &= \{x \in U | x \notin (A \cup B)\} \text{ (definition of complement) } \\[4pt] &= \{ x \in U | \neg(x \in A \cup B)\} \text{ (definiton of } \notin \text{) } \\[4pt] &= \{x \in U | \neg(x \in A \lor x \in B)\} \text{ (definition of } \cup \text{) } \\[4pt] &= \{x \in U | (\neg(x \in A)) \land (\neg(x \in B))\} \text{ (DeMorgan's Law for logic) } \\[4pt] &= \{x \in U | (x \notin A) \land (x \notin B)\} \text{ (definition of } \notin \text{) } \\[4pt] &= \{x \in U | (x \in \bar{A}) \land (x \in \bar{B})\} \text{ (definiton of complement) } \\[4pt] &= \bar{A} \cap \bar{B} \text{ ( definition of } \cap \text{) } \end{align*} \]
An easy inductive proof can be used to verify generalized versions of DeMorgan’s Laws for set theory. (In this context, all sets are assumed to be subsets of some unnamed universal set.) A simple calculation verifies DeMorgan’s Law for three sets:
\[ \begin{align*} \overline{A \cup B \cup C} &= \overline{(A \cup B) \cup C} \\[4pt] &= \overline{(A \cup B)} \cap \overline{C} \text{ (by DeMorgan's Law for two sets) } \\[4pt] &= (\overline{A} \cap \overline{B}) \cap \overline{C} \text{ (by DeMorgan's Law for two sets) } \\[4pt] &= \overline{A} \cap \overline{B} \cap \overline{C} \end{align*} \]
From there, we can derive similar laws for four sets, five sets, and so on. However, just saying “and so on” is not a rigorous proof of this fact. Here is a rigorous inductive proof of a generalized De Morgan’s Law:
Theorem 2.5: generalized De Morgan’s Law
For any natural number \(n ≥ 2\) and for any sets \(X_{1}, X_{2}, ..., X_{n}\),
\[\overline{X_{1} \cup X_{2} \cup ...\cup X_{n}} = \overline{X_{1}} \cap \overline{X_{2}} \cap ... \cap \overline{X_{n}}\]
Proof
We give a proof by induction. In the base case, \(n = 2\), the statement is that \(X_{1} ∪ X_{2} = X_{1} ∩ X_{n}\). This is true since it is just an application of DeMorgan’s law for two sets.
For the inductive case, suppose that the statement is true for \(n = k\). We want to show that it is true for \(n=k+1\). Let \(X_{1},X_{2},...,X_{k+1}\) be any \(k\) sets. Then we have:
\[ \begin{align*} \overline{X_{1} \cup X_{2} \cup ... \cup X_{k+1}} &= \overline{(X_{1} \cup X_{2} \cup ... \cup X_{k}) \cup X_{x+1}} \\[4pt] &= \overline{(X_{1} \cup X_{2} \cup ... \cup X_{k})} \cap \overline{X_{k+1}} \\[4pt] &= (\overline{X_{1}} \cap \overline{X_{2}} \cap ... \cap \overline{X_{k}}) \cap \overline{X_{k+1}} \\[4pt] &= \overline{X_{1}} \cap \overline{X_{2}} \cap ... \cap \overline{X_{k+1}} \end{align*} \]
In this computation, the second step follows by DeMorgan’s Law for two sets, while the third step follows from the induction hypothesis.
Just as the laws of logic allow us to do algebra with logical formulas, the laws of set theory allow us to do algebra with sets. Because of the close relationship between logic and set theory, their algebras are very similar. The algebra of sets, like the algebra of logic, is Boolean algebra. When George Boole wrote his 1854 book about logic, it was really as much about set theory as logic. In fact, Boole did not make a clear distinction between a predicate and the set of objects for which that predicate is true. His algebraic laws and formulas apply equally to both cases. More exactly, if we consider only subsets of some given universal set U , then there is a direct correspondence between the basic symbols and operations of propositional logic and certain symbols and operations in set theory, as shown in this table:
| Logic | Set Theory |
|---|---|
| \(\mathbb{T}\) | \(U\) |
| \(\mathbb{F}\) | \(\emptyset\) |
| \(p \land q\) | \(A \cap B\) |
| \(p \lor q\) | \(A \cup B\) |
| \(\neg p\) | \(\overline{A}\) |
Any valid logical formula or computation involving propositional variables and the symbols \(\mathbb{T}, \mathbb{F}, ∧, ∨,\) and \(¬\) can be transformed into a valid formula or computation in set theory by replacing the propositions in the formula with subsets of \(U\) and replacing the logical symbols with \(U, ∅, ∩, ∪,\) and the complement operator.
Just as in logic, the operations of set theory can be combined to form complex expressions such as \((A∪C)∩ \overline{(B ∪ \overline{C} ∪ D)}\). Parentheses can always be used in such expressions to specify the order in which the operations are to be performed. In the absence of parentheses, we need precedence rules to determine the order of operation. The precedence rules for the Boolean algebra of sets are carried over directly from the Boolean algebra of propositions. When union and intersection are used together without parentheses, intersection has precedence over union. Furthermore, when several operators of the same type are used without parentheses, then they are evaluated in order from left to right. (Of course, since \(∪\) and \(∩\) are both associative operations, it really doesn’t matter whether the order of evaluation is left-to-right or right-to-left.) For example, \(A ∪ B ∩ C ∪ D\) is evaluated as \((A ∪ ((B ∩ C)) ∪ D\). The complement operation is a special case. Since it is denoted by drawing a line over its operand, there is never any ambiguity about which part of a formula it applies to.
The laws of set theory can be used to simplify complex expressions involving sets. (As usual, of course, the meaning of “simplification” is partly in the eye of the beholder.) For example, for any sets \(X\) and \(Y\),
\[ \begin{align*} (X∪Y)∩(Y ∪X)&=(X∪Y)∩(X∪Y) \text{ (CommutativeLaw) } \\[4pt] &= (X ∪ Y ) \text{ (Idempotent Law) } \end{align*} \]
where in the second step, the Idempotent Law, which says that \(A ∩ A = A\), is applied with \(A = X ∪ Y\) . For expressions that use the complement operation, it is usually considered to be simpler to apply the operation to an individual set, as in \(A\), rather than to a formula, as in \(A ∩ B\). DeMorgan’s Laws can always be used to simplify an expression in which the complement operation is applied to a formula. For example,
\[A \cap \overline{B \cup \overline{A}} = A \cap (\overline{B} \cap \overline{\overline{A}}) \text{ (DeMorgan’s Law) } \nonumber\]
\[= A ∩ (\overline{B} ∩ A) \text{ (Double Complement) } \nonumber\]
\[= A ∩ (A ∩ \overline{B}) \text{ (Commutative Law) } \nonumber\]
\[= (A ∩ A) ∩ \overline{B}) \text{ (Associative Law) } \nonumber\]
\[=A∩ \overline{B} \text{ (Idempotent Law) } \nonumber\]
As a final example of the relationship between set theory and logic, consider the set-theoretical expression \(A ∩ (A ∪ B)\) and the corresponding compound proposition \(p ∧ (p ∨ q)\). (These correspond since for any \(x,x ∈ A∩(A∪B) ≡ (x ∈ A)∧((x ∈ A)∨(x ∈ B)).)\) You might find it intuitively clear that \(A ∩ (A ∪ B) = A\). Formally, this follows from the fact that \(p ∧ (p ∨ q) ≡ p\), which might be less intuitively clear and is surprising difficult to prove algebraically from the laws of logic. However, there is another way to check that a logical equivalence is valid: Make a truth table. Consider a truth table for \(p ∧ (p ∨ q)\):
| \(p\) | \(q\) | \(p \lor q\) | \(p \land (p \lor q)\) |
|---|---|---|---|
| false | false | false | false |
| false | true | true | false |
| true | false | true | true |
| true | true | true | true |
The fact that the first column and the last column of this table are identical shows that \(p∧(p∨q)≡p\). Taking \(p\) to be the proposition \(x∈A\) and \(q\) to be the proposition \(x ∈ B\), it follows that the sets \(A\) and \(A ∩ (A ∪ B)\) have the same members and therefore are equal.
Exercises
- Use the laws of logic to verify the associative laws for union and intersection. That is, show that if \(A, B,\) and \(C\) are sets, then \(A ∪ (B ∪ C) = (A ∪ B) ∪ C\) and \(A ∩ (B ∩ C) = (A ∩ B) ∩ C\).
- Show that for any sets \(A\) and \(B\), \(A ⊆ A ∪ B\) and \(A ∩ B ⊆ A\).
- Recall that the symbol ⊕ denotes the logical exclusive or operation. If \(A\) and \(B\) sets, define the set \(A△B\) by \(A△B\) = \(\{x|(x ∈ A)⊕(x ∈ B)\}\). Show that \(A△B=(A \setminus B)∪(B \setminus A).\) \((A△B\) is known as the symmetric difference of \(A\) and \(B\).)
- Let \(A\) be a subset of some given universal set \(U\). Verify that \(A = A\) and that \(A ∪ A = U\).
- Verify the second of DeMorgan’s Laws for sets, \(\overline{A ∩ B} = \overline{A} ∪ \overline{B}\). For each step in your verification, state why that step is valid.
- The subset operator, \(⊆\), is defined in terms of the logical implication operator, \(→\). However, \(⊆\) differs from the \(∩\) and \(∪\) operators in that \(A ∩ B\) and \(A ∪ B\) are sets, while \(A ⊆ B\) is a statement. So the relationship between \(⊆\) and \(→\) isn’t quite the same as the relationship between \(∪\) and \(∨\) or between \(∩\) and \(∧\). Nevertheless, \(⊆\) and \(→\) do share some similar properties. This problem shows one example.
a) Show that the following three compound propositions are logically equivalent: \(p→q,(p∧q)↔p\), and \((p∨q)↔q\).
b) Show that for any sets \(A\) and \(B\), the following three statements are equivalent: \(A⊆B\), \(A∩B=A\), and \(A∪B=B\). - DeMorgan’s Laws apply to subsets of some given universal set \(U\). Show that for a subset \(X\) of \(U\), \(\overline{X} = U \setminus X\). It follows that DeMorgan’s Laws can be written as \(U \setminus (A∪B) = (U \setminus A)∩(U \setminus B)\) and \(U \setminus (A∩B) = (U \setminus A)∪(U \setminus B)\). Show that these laws hold whether or not \(A\) and \(B\) are subsets of \(U\). That is, show that for any sets \(A, B,\) and \(C, C \setminus (A∪B) = (C \setminus A)∩(C \setminus B)\) and \(C \setminus (A ∩ B) = (C \setminus A) ∪ (C \setminus B)\).
- Show that \(A ∪ (A ∩ B)\) = \(A\) for any sets \(A\) and \(B\).
- Let \(X\) and \(Y\) be sets. Simplify each of the following expressions. Justify each step in the simplification with one of the rules of set theory.
a) \(X ∪ (Y ∪ X)\)
b) \((X ∩ Y ) ∩ \overline{X}\)
c) \((X ∪Y)∩ \overline{Y}\)
d) \((X ∪Y)∪(X ∩Y)\) - Let \(A, B,\) and \(C\) be sets. Simplify each of the following expressions. In your answer, the complement operator should only be applied to the individual sets \(A, B,\) and \(C\).
a) \(\overline{A \cup B \cup C}\)
b) \(\overline{A \cup B \cap B}\)
c) \(\overline{\overline{A \cup B}}\)
d) \(\overline{B \cap \overline{C}}\)
e) \(\overline{A \cap \overline{B \cap \overline{C}}}\)
f) \(A \cap \overline{A \cup B}\) - Use induction to prove the following generalized DeMorgan’s Law for set theory: For any natural number \(n ≥ 2\) and for any sets \(X_{1}, X_{2}, . . . , X_{n},\)
\(\overline{X_{1} \cap X_{2} \cap ... \cap X_{n}} = \overline{X_{1}} \cup \overline{X_{2}} \cup .... \cup \overline{X_{n}}\) - State and prove generalized distributive laws for set theory.


