8.2: The Greatest Common Divisor

A common divisor of \(a\) and \(b\) is a number that divides them both. The greatest common divisor of \(a\) and \(b\) is written \(\text{gcd}(a, b)\). For example, \(\text{gcd}(18, 24) = 6\).

As long as \(a\) and \(b\) are not both 0, they will have a gcd. The gcd turns out to be very valuable for reasoning about the relationship between \(a\) and \(b\) and for reasoning about integers in general. We’ll be making lots of use of gcd’s in what follows.

Some immediate consequences of the definition of gcd are that for \(n>0\),

\[\nonumber \text{gcd}(n, n) = n, \quad \text{gcd}(n, 1) = 1, \quad \text{gcd}(n, 0) = 0\]

where the last equality follows from the fact that everything is a divisor of 0.

Euclid’s Algorithm

The first thing to figure out is how to find gcd’s. A good way called Euclid’s algorithm has been known for several thousand years. It is based on the following elementary observation.

Lemma 8.2.1. For \(b \neq 0\),

\[\nonumber \text{gcd}(a, b) = \text{gcd}(b, \text{rem}(a, b)).\]

Proof. By the Division Theorem 8.1.4,

\[\label{8.2.1} \nonumber a = qb + r\]

where \(r = \text{rem}(a, b)\). So \(a\) is a linear combination of \(b\) and \(r\), which implies that any divisor of \(b\) and \(r\) is a divisor of a by Lemma 8.1.2.2. Likewise, \(r\) is a linear combination, \(a - qb\), of \(a\) and \(b\), so any divisor of \(a\) and \(b\) is a divisor of \(r\). This means that \(a\) and \(b\) have the same common divisors as \(b\) and \(r\), and so they have the same greatest common divisor.\(\quad \blacksquare\)

Lemma 8.2.1 is useful for quickly computing the greatest common divisor of two numbers. For example, we could compute the greatest common divisor of 1147 and 899 by repeatedly applying it:

\[\begin{aligned}
\text{gcd}(1147,899) &=\text{gcd}(899, \underbrace{\text{rem}(1147,899)}_{=248}) \\
&=\text{gcd}(248, \text{rem}(899,248)=155) \\
&=\text{gcd}(155, \text{rem}(248,155)=93) \\
&=\text{gcd}(93, \text{rem}(155,93)=62) \\
&=\text{gcd}(62, \text{rem}(93,62)=31) \\
&=\text{gcd}(31, \text{rem}(62,31)=0) \\
&=31
\end{aligned}\]

This calculation that \(\text{gcd}(1147, 899) = 31\) was how we figured out that with water jugs of sizes 1147 and 899, Bruce dies trying to get 32 gallons.

On the other hand, applying Euclid’s algorithm to 26 and 21 gives

\[\nonumber \text{gcd}(26, 21) = \text{gcd}(21, 5) = \text{gcd}(5, 1) = 1.\]

so we can’t use the reasoning above to rule out Bruce getting 3 gallons into the big jug. As a matter of fact, because the gcd here is 1, Bruce will be able to get any number of gallons into the big jug up to its capacity. To explain this, we will need a little more number theory.

Euclid’s Algorithm as a State Machine

Euclid’s algorithm can easily be formalized as a state machine. The set of states is \(\mathbb{N}^2\) and there is one transition rule:

\[\label{8.2.2} (x, y) \longrightarrow (y, \text{rem}(x, y)), \]

for \(y>0\). By Lemma 8.2.1, the gcd stays the same from one state to the next. That means the predicate

\[\nonumber \text{gcd}(x, y) = \text{gcd}(a, b).\]

is a preserved invariant on the states \((x, y)\). This preserved invariant is, of course, true in the start state \((a, b)\). So by the Invariant Principle, if \(y\) ever becomes 0, the invariant will be true and so

\[\nonumber x = \text{gcd}(x, 0) = \text{gcd}(a, b).\]

Namely, the value of \(x\) will be the desired gcd.

What’s more, \(x\), and therefore also \(y\), gets to be 0 pretty fast. To see why, note that starting from \((x, y)\), two transitions leads to a state whose the first coordinate is \(\text{rem}(x, y)\), which is at most half the size of x.³ Since \(x\) starts off equal to \(a\) and gets halved or smaller every two steps, it will reach its minimum value—which is \(\text{gcd}(a, b)\)—after at most 2 log \(a\) transitions. After that, the algorithm takes at most one more transition to terminate. In other words, Euclid’s algorithm terminates after at most \(1 + 2\) log \(a\) transitions.⁴

The Pulverizer

We will get a lot of mileage out of the following key fact:

Theorem \(\PageIndex{2}\)

The greatest common divisor of \(a\) and \(b\) is a linear combination of \(a\) and \(b\). That is,

\[\nonumber \text{gcd}(a, b) = sa + tb,\]

for some integers \(s\) and \(t\).

We already know from Lemma 8.1.2.2 that every linear combination of \(a\) and \(b\) is divisible by any common factor of \(a\) and \(b\), so it is certainly divisible by the greatest of these common divisors. Since any constant multiple of a linear combination is also a linear combination, Theorem 8.2.2 implies that any multiple of the gcd is a linear combination, giving:

Corollary 8.2.3. An integer is a linear combination of \(a\) and \(b\) iff it is a multiple of \(\text{gcd}(a, b)\).

We’ll prove Theorem 8.2.2 directly by explaining how to find \(s\) and \(t\). This job is tackled by a mathematical tool that dates back to sixth-century India, where it was called kuttak, which means “The Pulverizer.” Today, the Pulverizer is more commonly known as “the extended Euclidean gcd algorithm,” because it is so close to Euclid’s algorithm.

For example, following Euclid’s algorithm, we can compute the gcd of 259 and 70 as follows:

\[\nonumber \begin{array}{l}
\text{gcd}(259, 70) &=\text{gcd}(70, 49) & \text{since rem}(259, 70) = 49\\
&=\text{gcd}(49, 21) & \text{since rem}(70, 49) = 21\\
&=\text{gcd}(21, 7) & \text{since rem}(49, 21) = 7 \\
&=\text{gcd}(7, 0) & \text{since rem}(21, 7) = 0 \\
&=7.
\end{array}\]

The Pulverizer goes through the same steps, but requires some extra bookkeeping along the way: as we compute \(\text{gcd}(a, b)\), we keep track of how to write each of the remainders (49, 21, and 7, in the example) as a linear combination of \(a\) and \(b\). This is worthwhile, because our objective is to write the last nonzero remainder, which is the GCD, as such a linear combination. For our example, here is this extra bookkeeping:

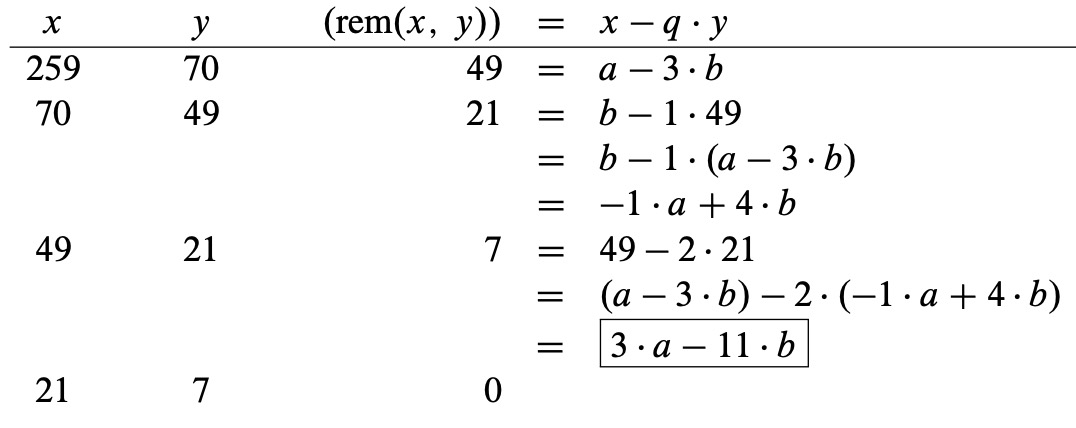
We began by initializing two variables, \(x = a\) and \(y = b\). In the first two columns above, we carried out Euclid’s algorithm. At each step, we computed \(\text{rem}(x, y)\) which equals \(x - \text{qcnt}(x, y) \cdot y\). Then, in this linear combination of \(x\) and \(y\), we replaced \(x\) and \(y\) by equivalent linear combinations of \(a\) and \(b\), which we already had computed. After simplifying, we were left with a linear combination of \(a\) and \(b\) equal to \(\text{rem}(x, y)\), as desired. The final solution is boxed.

This should make it pretty clear how and why the Pulverizer works. If you have doubts, it may help to work through Problem 8.13, where the Pulverizer is formalized as a state machine and then verified using an invariant that is an extension of the one used for Euclid’s algorithm.

Since the Pulverizer requires only a little more computation than Euclid’s algorithm, you can “pulverize” very large numbers very quickly by using this algorithm. As we will soon see, its speed makes the Pulverizer a very useful tool in the field of cryptography.

Now we can restate the Water Jugs Lemma 8.1.5 in terms of the greatest common divisor:

Corollary 8.2.4. Suppose that we have water jugs with capacities \(a\) and \(b\). Then the amount of water in each jug is always a multiple of \(\text{gcd}(a, b)\).

For example, there is no way to form 4 gallons using 3- and 6-gallon jugs, because 4 is not a multiple of \(\text{gcd}(3, 6) = 3\).

One Solution for All Water Jug Problems

Corollary 8.2.3 says that 3 can be written as a linear combination of 21 and 26, since 3 is a multiple of \(\text{gcd}(21, 26) = 1\). So the Pulverizer will give us integers \(s\) and \(t\) such that

\[\label{8.2.3} 3 = s \cdot 21 + t \cdot 26\]

The coefficient \(s\) could be either positive or negative. However, we can readily transform this linear combination into an equivalent linear combination

\[\label{8.2.4} 3 = s' \cdot 21 + t' \cdot 26\]

where the coefficient \(s'\) is positive. The trick is to notice that if in equation (\ref{8.2.3}) we increase \(s\) by 26 and decrease \(t\) by 21, then the value of the expression \(s \cdot 21 + t \cdot 26\) is unchanged overall. Thus, by repeatedly increasing the value of \(s\) (by 26 at a time) and decreasing the value of \(t\) (by 21 at a time), we get a linear combination \(s' \cdot 21 + t' \cdot 26 = 3\) where the coefficient \(s'\) is positive. (Of course \(t'\) must then be negative; otherwise, this expression would be much greater than 3.)

Now we can form 3 gallons using jugs with capacities 21 and 26: We simply repeat the following steps \(s'\) times:

1. Fill the 21-gallon jug.
2. Pour all the water in the 21-gallon jug into the 26-gallon jug. If at any time the 26-gallon jug becomes full, empty it out, and continue pouring the 21- gallon jug into the 26-gallon jug.

At the end of this process, we must have emptied the 26-gallon jug exactly \(t'\) times. Here’s why: we’ve taken \(s' \cdot 21\) gallons of water from the fountain, and we’ve poured out some multiple of 26 gallons. If we emptied fewer than \(t'\) times, then by (\ref{8.2.4}), the big jug would be left with at least \(3 + 26\) gallons, which is more than it can hold; if we emptied it more times, the big jug would be left containing at most \(3 - 26\) gallons, which is nonsense. But once we have emptied the 26-gallon jug exactly \(-t'\) times, equation (\ref{8.2.4}) implies that there are exactly 3 gallons left.

Remarkably, we don’t even need to know the coefficients \(s'\) and \(t'\) in order to use this strategy! Instead of repeating the outer loop \(s'\) times, we could just repeat until we obtain 3 gallons, since that must happen eventually. Of course, we have to keep track of the amounts in the two jugs so we know when we’re done. Here’s the solution using this approach starting with empty jugs, that is, at (0, 0):

The same approach works regardless of the jug capacities and even regardless of the amount we’re trying to produce! Simply repeat these two steps until the desired amount of water is obtained:

1. Fill the smaller jug.
2. Pour all the water in the smaller jug into the larger jug. If at any time the larger jug becomes full, empty it out, and continue pouring the smaller jug into the larger jug.

By the same reasoning as before, this method eventually generates every multiple— up to the size of the larger jug—of the greatest common divisor of the jug capacities, all the quantities we can possibly produce. No ingenuity is needed at all!

So now we have the complete water jug story:

Theorem \(\PageIndex{5}\)

Suppose that we have water jugs with capacities \(a\) and \(b\). For any \(c \in [0..a]\), it is possible to get \(c\) gallons in the size \(a\) jug iff \(c\) is a multiple of \(\text{gcd}(a, b)\).

 

³In other words,

\[\text{rem}(x, y) \leq x/2 \quad \text{for } 0 < y \leq x.\]

This is immediate if \(y \leq x/2\), since the remainder of \(x\) divided by \(y\) is less than \(y\) by definition. On the other hand, if \(y > x/2\), then \(\text{rem}(x, y) = x - y < x/2\).

⁴A tighter analysis shows that at most \(\text{log}_{\phi}(a)\) transitions are possible where \(\phi\) is the golden ratio \((1 + \sqrt{5}) / 2\), see Problem 8.14.