14.7: Counting Practice - Poker Hands

Five-Card Draw is a card game in which each player is initially dealt a hand consisting of 5 cards from a deck of 52 cards.³ The number of different hands in Five-Card Draw is the number of 5-element subsets of a 52-element set, which is

\[\nonumber {52 \choose 5} = \text{2,598,960}.\]

Let’s get some counting practice by working out the number of hands with various special properties.

Hands with a Four-of-a-Kind

A Four-of-a-Kind is a set of four cards with the same rank. How many different hands contain a Four-of-a-Kind? Here are a couple examples:

\[\begin{aligned} \{8\spadesuit, 8\diamondsuit, Q\heartsuit, 8\heartsuit, 8\clubsuit\} \\ \{A\clubsuit, 2\clubsuit, 2\heartsuit, 2\diamondsuit, 2\spadesuit\} \end{aligned}\]

As usual, the first step is to map this question to a sequence-counting problem. A hand with a Four-of-a-Kind is completely described by a sequence specifying:

1. The rank of the four cards.
2. The rank of the extra card.
3. The suit of the extra card.

Thus, there is a bijection between hands with a Four-of-a-Kind and sequences consisting of two distinct ranks followed by a suit. For example, the three hands above are associated with the following sequences:

\[\begin{aligned} (8, Q, \heartsuit) \leftrightarrow \{8\spadesuit, 8\diamondsuit, 8\heartsuit, 8\clubsuit, Q\heartsuit\} \\ (2, A, \clubsuit) \leftrightarrow \{ 2\clubsuit, 2\heartsuit, 2\diamondsuit, 2\spadesuit, A\clubsuit\} \end{aligned}\]

Now we need only count the sequences. There are 13 ways to choose the first rank, 12 ways to choose the second rank, and 4 ways to choose the suit. Thus, by the Generalized Product Rule, there are \(13 \cdot 12 \cdot 4 = 624\) hands with a Four-of-a-Kind. This means that only 1 hand in about 4165 has a Four-of-a-Kind. Not surprisingly, Four-of-a-Kind is considered to be a very good poker hand!

Hands with a Full House

A Full House is a hand with three cards of one rank and two cards of another rank. Here are some examples:

\[\begin{aligned} \{2\spadesuit, 2\clubsuit, 2\diamondsuit, J\clubsuit, J\diamondsuit\} \\ \{5\diamondsuit, 5\clubsuit, 5\heartsuit, 7\heartsuit, 7\clubsuit\} \end{aligned}\]

Again, we shift to a problem about sequences. There is a bijection between Full Houses and sequences specifying:

1. The rank of the triple, which can be chosen in 13 ways.
2. The suits of the triple, which can be selected in \({4 \choose 3}\) ways.
3. The rank of the pair, which can be chosen in 12 ways.
4. The suits of the pair, which can be selected in \({4 \choose 2}\) ways.

The example hands correspond to sequences as shown below:

\[\begin{aligned} (2, \{\spadesuit, \clubsuit, \diamondsuit\}, J, \{\clubsuit, \diamondsuit\}) &\leftrightarrow \{2\spadesuit, 2\clubsuit, 2\diamondsuit, J\clubsuit, J\diamondsuit\}\\ (5, \{\diamondsuit, \clubsuit, \heartsuit\}, 7, \{\heartsuit, \clubsuit\}) &\leftrightarrow \{5\diamondsuit, 5\clubsuit, 5\heartsuit, 7\heartsuit, 7\clubsuit\} \end{aligned}\]

By the Generalized Product Rule, the number of Full Houses is:

\[\nonumber 13 \cdot {4 \choose 3} \cdot 12 \cdot {4 \choose 2}\]

We’re on a roll—but we’re about to hit a speed bump.

Hands with Two Pairs

How many hands have Two Pairs; that is, two cards of one rank, two cards of another rank, and one card of a third rank? Here are examples:

\[\begin{aligned} \{3\diamondsuit, 3\spadesuit, Q\diamondsuit, Q\heartsuit, A\clubsuit\} \\ \{9\heartsuit, 9\diamondsuit, 5\heartsuit, 5\clubsuit, K\spadesuit\} \end{aligned}\]

Each hand with Two Pairs is described by a sequence consisting of:

1. The rank of the first pair, which can be chosen in 13 ways.
2. The suits of the first pair, which can be selected \({4 \choose 2}\) ways.
3. The rank of the second pair, which can be chosen in 12 ways.
4. The suits of the second pair, which can be selected in \({4 \choose 2}\) ways.
5. The rank of the extra card, which can be chosen in 11 ways.
6. The suit of the extra card, which can be selected in \({4 \choose 1} = 4\) ways.

Thus, it might appear that the number of hands with Two Pairs is:

\[\nonumber 13 \cdot {4 \choose 2} \cdot 12 \cdot {4 \choose 2} \cdot 11 \cdot 4.\]

Wrong answer! The problem is that there is not a bijection from such sequences to hands with Two Pairs. This is actually a 2-to-1 mapping. For example, here are the pairs of sequences that map to the hands given above:

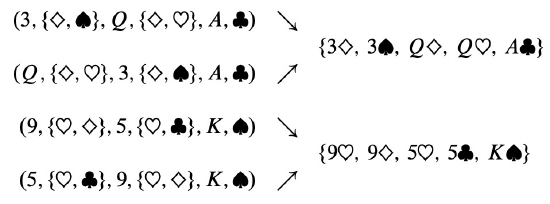
The problem is that nothing distinguishes the first pair from the second. A pair of 5’s and a pair of 9’s is the same as a pair of 9’s and a pair of 5’s. We avoided this difficulty in counting Full Houses because, for example, a pair of 6’s and a triple of kings is different from a pair of kings and a triple of 6’s.

We ran into precisely this difficulty last time, when we went from counting arrangements of different pieces on a chessboard to counting arrangements of two identical rooks. The solution then was to apply the Division Rule, and we can do the same here. In this case, the Division rule says there are twice as many sequences as hands, so the number of hands with Two Pairs is actually:

\[\nonumber \dfrac{13 \cdot {4 \choose 2} \cdot 12 \cdot {4 \choose 2} \cdot 11 \cdot 4}{2}.\]

Another Approach

The preceding example was disturbing! One could easily overlook the fact that the mapping was 2-to-1 on an exam, fail the course, and turn to a life of crime. You can make the world a safer place in two ways:

1. Whenever you use a mapping \(f : A \rightarrow B\) to translate one counting problem to another, check that the same number of elements in \(A\) are mapped to each element in \(B\). If \(k\) elements of \(A\) map to each of element of \(B\), then apply the Division Rule using the constant \(k\).
2. As an extra check, try solving the same problem in a different way. Multiple approaches are often available—and all had better give the same answer! (Sometimes different approaches give answers that look different, but turn out to be the same after some algebra.)

We already used the first method; let’s try the second. There is a bijection between hands with two pairs and sequences that specify:

1. The ranks of the two pairs, which can be chosen in \({13 \choose 2}\) ways.
2. The suits of the lower-rank pair, which can be selected in \({4 \choose 2}\) ways.
3. The suits of the higher-rank pair, which can be selected in \({4 \choose 2}\) ways.
4. The rank of the extra card, which can be chosen in 11 ways.
5. The suit of the extra card, which can be selected in \({4 \choose 1} = 4\) ways.

For example, the following sequences and hands correspond:

\[\begin{aligned} (\{3, Q\}, \{\diamondsuit, \spadesuit\}, \{\diamondsuit, \heartsuit\}, A, \clubsuit) &\leftrightarrow \{3\diamondsuit, 3\spadesuit, Q\diamondsuit, Q\heartsuit, A\clubsuit\}\\ (\{9, 5\}, \{\heartsuit, \clubsuit\}, \{\heartsuit, \diamondsuit\}, K, \spadesuit) &\leftrightarrow \{9\heartsuit, 9\diamondsuit, 5\heartsuit, 5\clubsuit, K\spadesuit\} \end{aligned} \]

Thus, the number of hands with two pairs is:

\[\nonumber {13 \choose 2} \cdot {4 \choose 2} \cdot {4 \choose 2} \cdot 11 \cdot 4.\]

This is the same answer we got before, though in a slightly different form.

Hands with Every Suit

How many hands contain at least one card from every suit? Here is an example of such a hand:

\[\nonumber \{7\diamondsuit, K\clubsuit, 3\diamondsuit, A\heartsuit, 2\spadesuit\}\]

Each such hand is described by a sequence that specifies:

1. The ranks of the diamond, the club, the heart, and the spade, which can be selected in \(13 \cdot 13 \cdot 13 \cdot 13 = 13^4\) ways.
2. The suit of the extra card, which can be selected in 4 ways.
3. The rank of the extra card, which can be selected in 12 ways.

For example, the hand above is described by the sequence:

\[\nonumber (7, K, A, 2, \diamondsuit, 3) \leftrightarrow \{7\diamondsuit, K\clubsuit, A\heartsuit, 2\spadesuit, 3\diamondsuit\}.\]

Are there other sequences that correspond to the same hand? There is one more! We could equally well regard either the \(3\diamondsuit\) or the \(7\diamondsuit\) as the extra card, so this is actually a 2-to-1 mapping. Here are the two sequences corresponding to the example hand:

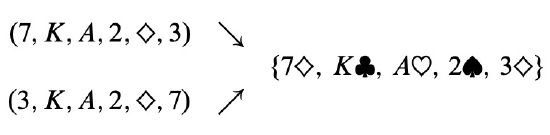
Therefore, the number of hands with every suit is:

\[\nonumber \dfrac{13^4 \cdot 4 \cdot 12}{2}.\]

³There are 52 cards in a standard deck. Each card has a suit and a rank. There are four suits: 

\(\spadesuit\) (spades) \(\heartsuit\) (hearts) \(\clubsuit\) (clubs) \(\diamondsuit\) (diamonds)

And there are 13 ranks, listed here from lowest to highest:

\[\nonumber \overset{\text{Ace}}{A}, 2, 3, 4, 5, 6, 7, 8, 9, \overset{\text{Jack}}{J}, \overset{\text{Queen}}{Q}, \overset{\text{King}}{K}.\]

Thus, for example, \(8\heartsuit\) is the 8 of hearts and \(A\spadesuit\) is the ace of spades.