15.4: Solving Linear Recurrences

Generating Function for the Fibonacci Numbers

The Fibonacci numbers \(f_0, f_1, \ldots, f_n, \ldots\) are defined recursively as follows:

\[\begin{aligned} f_0 &::= 0 \\ f_1 &::= 1 \\ f_n &= :: = f_{n-1} + f_{n-2} & (\text{for } n \geq 2). \end{aligned}\]

Generating functions will now allow us to derive an astonishing closed formula for \(f_n.\)

Let \(F(x)\) be the generating function for the sequence of Fibonacci numbers, that is,

\[\nonumber F(x) ::= f_0 + f_1 x + f_2 x^2 + \cdots + f_n x^n + \cdots .\]

Reasoning as we did at the start of this chapter to derive the formula for a geometric series, we have

\[\nonumber \begin{array}{c=cccccccccccc}
F(x) &= & f_0 & + & f_1x & + & f_2x^2 & + & \cdots & + & f_nx^n & + & \cdots. \\ -xF(x) &= & & - & f_0x & - & f_1x^2 & - & \cdots & - & f_{n-1}x^n & + & \cdots. \\ -x^2F(x) &= & & & & - & f_0x^2 & - & \cdots & - & f_{n-2}x^n & + & \cdots.\\
\hline F(x)(1-x-x^2) &= & f_0 & + & (f_1 - f_0)x & + & 0x^2 & + & \cdots & + & 0x^n & + &\cdots. \\
&= & 0 & + & 1x & + & 0x^2 &= &x, & & & &
\end{array}\]

so

\[\nonumber F(x) = \dfrac{x}{1 - x - x^2}.\]

But \(F(x)\) is the same as the function we used to illustrate the partial fraction method for finding coefficients in Section 15.3. So by equation (15.3.2), we arrive at what is called Binet’s formula:

\[\label{15.4.1} f_n = \dfrac{1}{\sqrt{5}}\left (\left( \dfrac{1 + \sqrt{5}}{2}\right)^n - \left( \dfrac{1 - \sqrt{5}}{2}\right)^n \right)\]

Binet’s formula for Fibonacci numbers is astonishing and maybe scary. It’s not even obvious that the expression on the right hand side (\ref{15.4.1}) is an integer. But the formula is very useful. For example, it provides—via the repeated squaring method—a much more efficient way to compute Fibonacci numbers than crunching through the recurrence. It also make explicit the exponential growth of these numbers.

The Towers of Hanoi

According to legend, there is a temple in Hanoi with three posts and 64 gold disks of different sizes. Each disk has a hole through the center so that it fits on a post. In the misty past, all the disks were on the first post, with the largest on the bottom and the smallest on top, as shown in Figure 15.1.

Figure 15.1 The initial configuration of the disks in the Towers of Hanoi problem.

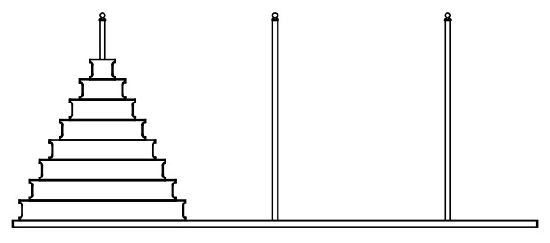
Monks in the temple have labored through the years since to move all the disks to one of the other two posts according to the following rules:

• The only permitted action is removing the top disk from one post and dropping it onto another post.
• A larger disk can never lie above a smaller disk on any post.

So, for example, picking up the whole stack of disks at once and dropping them on another post is illegal. That’s good, because the legend says that when the monks complete the puzzle, the world will end!

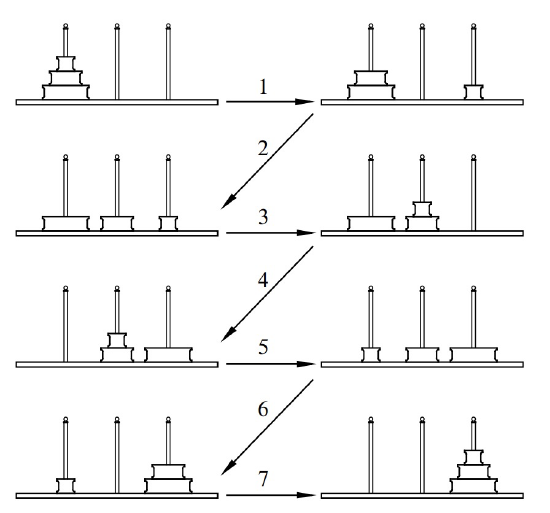
To clarify the problem, suppose there were only 3 gold disks instead of 64. Then the puzzle could be solved in 7 steps as shown in Figure 15.2.

The questions we must answer are, “Given sufficient time, can the monks succeed?” If so, “How long until the world ends?” And, most importantly, “Will this happen before the final exam?”

A Recursive Solution

The Towers of Hanoi problem can be solved recursively. As we describe the procedure, we’ll also analyze the minimum number, \(t_n\), of steps required to solve the \(n\)-disk problem. For example, some experimentation shows that \(t_1 = 1\) and \(t_2 = 3\). The procedure illustrated above uses 7 steps, which shows that \(t_3\) is at most 7.

The recursive solution has three stages, which are described below and illustrated in Figure 15.3. For clarity, the largest disk is shaded in the figures.

Figure 15.2 The 7-step solution to the Towers of Hanoi problem when there are \(n = 3\) disks.

Figure 15.3 A recursive solution to the Towers of Hanoi problem.

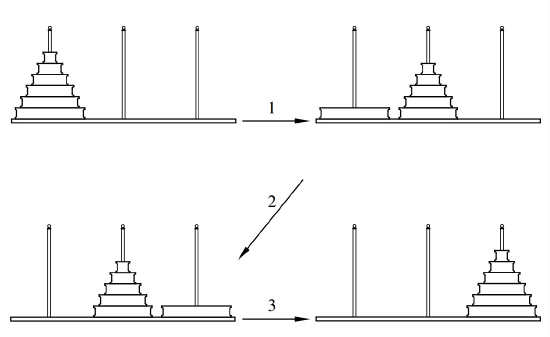
Stage 1. Move the top \(n - 1\) disks from the first post to the second using the solution for \(n - 1\) disks. This can be done in \(t_{n-1}\) steps.

Stage 2. Move the largest disk from the first post to the third post. This takes just 1 step.

Stage 3. Move the \(n - 1\) disks from the second post to the third post, again using the solution for \(n - 1\) disks. This can also be done in \(t_{n-1}\) steps.

This algorithm shows that \(t_{n}\), the minimum number of steps required to move \(n\) disks to a different post, is at most \(t_{n-1} + 1 + t_{n-1} = 2t_{n-1} + 1\). We can use this fact to upper bound the number of operations required to move towers of various heights:

\[\begin{aligned} t_3 &\leq 2 \cdot t_2 + 1 = 7 \\ t_4 &\leq 2 \cdot t_3 + 1 \leq 15 \end{aligned}\]

Continuing in this way, we could eventually compute an upper bound on \(t_{64}\), the number of steps required to move 64 disks. So this algorithm answers our first question: given sufficient time, the monks can finish their task and end the world. This is a shame. After all that effort, they’d probably want to smack a few high-fives and go out for burgers and ice cream, but nope—world’s over.

Finding a Recurrence

We cannot yet compute the exact number of steps that the monks need to move the 64 disks, only an upper bound. Perhaps, having pondered the problem since the beginning of time, the monks have devised a better algorithm

Lucky for us, there is no better algorithm. Here’s why: at some step, the monks must move the largest disk from the first post to a different post. For this to happen, the \(n - 1\) smaller disks must all be stacked out of the way on the only remaining post. Arranging the \(n - 1\) smaller disks this way requires at least \(t_{n-1}\) moves. After the largest disk is moved, at least another \(t_{n-1}\) moves are required to pile the \(n - 1\) smaller disks on top

This argument shows that the number of steps required is at least \(2t_{n-1} + 1\). Since we gave an algorithm using exactly that number of steps, we can now write an expression for \(t_n\), the number of moves required to complete the Towers of Hanoi problem with \(n\) disks:

\[\begin{aligned} t_0 &= 0 \\ t_n &= 2t_{n-1} + 1 & (\text{for } n \geq 1). \end{aligned}\]

Solving the Recurrence

We can now find a formula for \(t_n\) using generating functions. Let \(T(x)\) be the generating function for the \(t_n\)’s, that is,

\[\nonumber T(x) ::= t_0 + t_1x + t_2x^2 + \cdots + t_nx^n + \cdots.\]

Reasoning as we did for the Fibonacci recurrence, we have

\[\nonumber \begin{array}{c=cccccccccc}
T(x) &= & t_0 & + & t_1x & + & \cdots & + & t_nx^n & + & \cdots \\ -2xT(x) &= & & - & 2t_0x & - & \cdots & - & 2t_{n-1}x^n & + & \cdots \\ -1/(1-x) &= & -1 & - & -1x & - & \cdots & - & 1x^n & + & \cdots\\
\hline T(x)(1-2x)-1/(1-x) &= & t_0 - 1 & + & 0x & + & \cdots & + & 0x^n & + &\cdots \\
&= & -1, & & & & & & & &
\end{array}\]

so

\[\nonumber T(x)(1-2x) = \dfrac{1}{1-x} - 1 = \dfrac{x}{1-x},\]

and

\[\nonumber T(x) = \dfrac{x}{(1-2x)(1-x)}.\]

Using partial fractions,

\[\nonumber \dfrac{x}{(1-2x)(1-x)} = \dfrac{c_1}{1-2x} + \dfrac{c_2}{1-x}\]

for some constant \(c_1, c_2\). Now multiplying both sides by the left hand denominator gives

\[\nonumber x = c_1(1-x) + c_2(1-2x).\]

Substituting \(1/2\) for \(x\) yields \(c_1 = 1\) and substituting 1 for \(x\) yields \(c_2 = -1\), which gives

\[\nonumber T(x) = \dfrac{1}{1-2x} - \dfrac{1}{1-x}.\]

Finally we can read off the simple formula for the numbers of steps needed to move a stack of \(n\) disks:

\[\nonumber t_n = [x^n]T(x) = [x^n]\left(\dfrac{1}{1-2x}\right) - [x^n]\left(\dfrac{1}{1-x}\right) = 2^n - 1.\]

Solving General Linear Recurrences

An equation of the form

\[f(n) = c_1f(n-1) + c_2f(n-2) + \cdots + c_df(n-d) + h(n)\]

for constants \(c_i \in \mathbb{C}\) is called a degree \(d\) linear recurrence with inhomogeneous term \(h(n)\).

The methods above can be used to solve linear recurrences with a large class of inhomogeneous terms. In particular, when the inhomogeneous term itself has a generating function that can be expressed as a quotient of polynomials, the approach used above to derive generating functions for the Fibonacci and Tower of Hanoi examples carries over to yield a quotient of polynomials that defines the generating function \(f(0) + f(1)x + f(2)x^2 + \cdots\). Then partial fractions can be used to find a formula for \(f(n)\) that is a linear combination of terms of the form \(n^k \alpha^n\) where \(k\) is a nonnegative integer \(\leq d\) and \(\alpha\) is the reciprocal of a root of the denominator polynomial. For example, see Problems 15.15, 15.16, 15.20, and 15.21.