3.4: Problems
- Page ID
- 18953
3.1. For each of the three crystalline materials below
- Find the crystal point group to which it belongs. (Hint: use http://www.mindat.org )
- Using Table 2.3.1, determine whether or not the material is piezoelectric.
- Using Table 2.3.1, determine whether or not the material is pyroelectric.
- Using Table 2.3.1, determine whether or not the material is Pockels electro-optic.
(a) ZnS (sphalerite)
(b) HgS (cinnabar)
(c) Diamond
3.2. Cane sugar, also called saccharose, has chemical composition C\(_12\)H\(_22\)O\(_11\) and belongs to the crystal point group given by 2 in Hermann-Maguin notation [38]. Reference [38] lists values specified in cgse units for its piezoelectric constant as \(10.2 \cdot 10^{-8} \frac{\text{esu}}{\text{dyne}}\) and its pyroelectric coefficient as \(0.53 \frac{\text{esu}}{cm^2 \cdot ^{\circ}\text{C}}\). Convert these values to the SI units of \(\frac{m}{V}\) and \(\frac{C}{m^2\cdot K}\) respectively.
Hint: The electrostatic unit or statcoulomb is a measure of charge [7] where \[ 1 \text{ esu} = 1 \text{ statC} = 3.335641 \cdot 10^{-10} C \nonumber \] and the dyne is a measure of force where \( 1 \text{ dyne} = 10^{-5} N \).
3.3. A material has relative permittivity \(\epsilon_{r\;x}\) when no external electric field is applied. The coefficient \(\chi^{(2)}\) is measured in the presence of an external electric field of strength \(|\overrightarrow{E}|\). Assume that \(\chi^{(3)}\) and all higher order coefficients are zero. Find the Pockels coefficient \(\gamma\) as a function of the known quantities \(\epsilon_{r\;x}\), \(\chi^{(2)}\), and \(|\overrightarrow{E}|\).
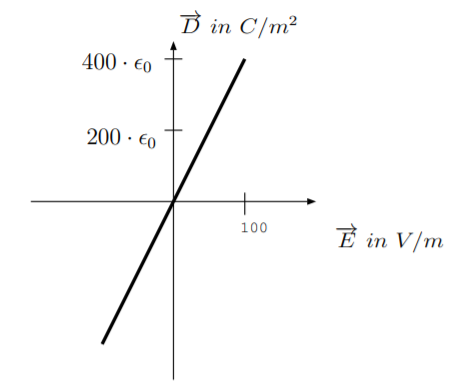
3.4. The first figure below shows the displacement flux density \(|\overrightarrow{D}|\) as a function of the strength of an applied electric field intensity \(|\overrightarrow{E}|\) in a non-electro-optic material. The second figure below shows the displacement flux density \(|\overrightarrow{D}|\) as a function of the strength of an applied electric field intensity \(|\overrightarrow{E}|\) in a ferroelectric electro-optic material. The solid line corresponds to an unpoled material. The dotted line corresponds to the material after it has been poled in the \(\hat{a}_z\) direction, and the dashed line corresponds to the material after it has been poled in the \(-\hat{a}_z\) direction.
(a) For the non-electro-optic material, find the relative permittivity, \(\epsilon_r\). Also find the magnitude of the material polarization, \(\overrightarrow{P}\).
(b) Assume the ferroelectric electro-optic material is poled by a strong external electric field, and then the field is removed. Find the magnitude of the material polarization \(|\overrightarrow{P}|\) after the external field is removed.
(c) Assume the ferroelectric material is poled in the \(-\hat{a}_z\) direction by a strong external field, and then the field is removed. A different external electric field given by \(\overrightarrow{E} = 100\hat{a}_z \frac{V}{m}\) is applied. Find the approximate relative permittivity of the material.

3.5. A crystalline material is both piezoelectric and pyroelectric. When an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) is applied, the material polarization is determined to be \(|\overrightarrow{P}| = 1500\epsilon_0 \frac{C}{m^2}\). When both a stress of \(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\) and an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) are applied, the material polarization is determined to be \(|\overrightarrow{P}| = 6.0123 \cdot 10^{-6} \frac{C}{m^2}\). When a temperature gradient of \(\Delta T = 50\; ^\circ C\), a stress of \(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\), and an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) are applied, the material polarization is determined to be \(|\overrightarrow{P}| = 6.3 \cdot 10^{-6} \frac{C}{m^2}\). Find:
- The relative permittivity of the material
- The piezoelectric strain constant
- The magnitude of the pyroelectric coefficient


