3.4: Problems
- Page ID
- 18953
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3.1. For each of the three crystalline materials below
- Find the crystal point group to which it belongs. (Hint: use http://www.mindat.org )
- Using Table 2.3.1, determine whether or not the material is piezoelectric.
- Using Table 2.3.1, determine whether or not the material is pyroelectric.
- Using Table 2.3.1, determine whether or not the material is Pockels electro-optic.
(a) ZnS (sphalerite)
(b) HgS (cinnabar)
(c) Diamond
3.2. Cane sugar, also called saccharose, has chemical composition C\(_12\)H\(_22\)O\(_11\) and belongs to the crystal point group given by 2 in Hermann-Maguin notation [38]. Reference [38] lists values specified in cgse units for its piezoelectric constant as \(10.2 \cdot 10^{-8} \frac{\text{esu}}{\text{dyne}}\) and its pyroelectric coefficient as \(0.53 \frac{\text{esu}}{cm^2 \cdot ^{\circ}\text{C}}\). Convert these values to the SI units of \(\frac{m}{V}\) and \(\frac{C}{m^2\cdot K}\) respectively.
Hint: The electrostatic unit or statcoulomb is a measure of charge [7] where \[ 1 \text{ esu} = 1 \text{ statC} = 3.335641 \cdot 10^{-10} C \nonumber \] and the dyne is a measure of force where \( 1 \text{ dyne} = 10^{-5} N \).
3.3. A material has relative permittivity \(\epsilon_{r\;x}\) when no external electric field is applied. The coefficient \(\chi^{(2)}\) is measured in the presence of an external electric field of strength \(|\overrightarrow{E}|\). Assume that \(\chi^{(3)}\) and all higher order coefficients are zero. Find the Pockels coefficient \(\gamma\) as a function of the known quantities \(\epsilon_{r\;x}\), \(\chi^{(2)}\), and \(|\overrightarrow{E}|\).
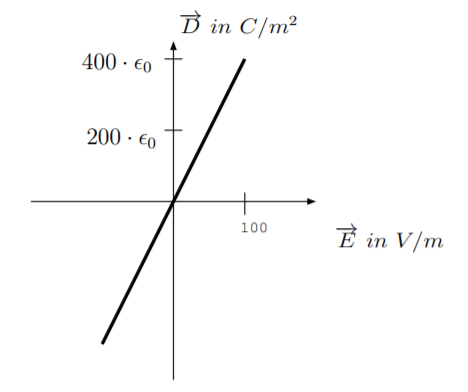
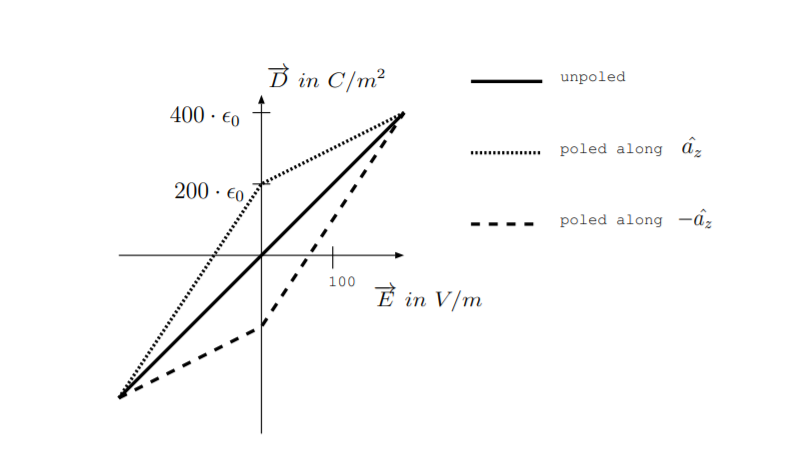
3.4. The first figure below shows the displacement flux density \(|\overrightarrow{D}|\) as a function of the strength of an applied electric field intensity \(|\overrightarrow{E}|\) in a non-electro-optic material. The second figure below shows the displacement flux density \(|\overrightarrow{D}|\) as a function of the strength of an applied electric field intensity \(|\overrightarrow{E}|\) in a ferroelectric electro-optic material. The solid line corresponds to an unpoled material. The dotted line corresponds to the material after it has been poled in the \(\hat{a}_z\) direction, and the dashed line corresponds to the material after it has been poled in the \(-\hat{a}_z\) direction.
(a) For the non-electro-optic material, find the relative permittivity, \(\epsilon_r\). Also find the magnitude of the material polarization, \(\overrightarrow{P}\).
(b) Assume the ferroelectric electro-optic material is poled by a strong external electric field, and then the field is removed. Find the magnitude of the material polarization \(|\overrightarrow{P}|\) after the external field is removed.
(c) Assume the ferroelectric material is poled in the \(-\hat{a}_z\) direction by a strong external field, and then the field is removed. A different external electric field given by \(\overrightarrow{E} = 100\hat{a}_z \frac{V}{m}\) is applied. Find the approximate relative permittivity of the material.
3.5. A crystalline material is both piezoelectric and pyroelectric. When an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) is applied, the material polarization is determined to be \(|\overrightarrow{P}| = 1500\epsilon_0 \frac{C}{m^2}\). When both a stress of \(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\) and an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) are applied, the material polarization is determined to be \(|\overrightarrow{P}| = 6.0123 \cdot 10^{-6} \frac{C}{m^2}\). When a temperature gradient of \(\Delta T = 50\; ^\circ C\), a stress of \(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\), and an external electric field of \(|\overrightarrow{E}| = 100 \frac{V}{m}\) are applied, the material polarization is determined to be \(|\overrightarrow{P}| = 6.3 \cdot 10^{-6} \frac{C}{m^2}\). Find:
- The relative permittivity of the material
- The piezoelectric strain constant
- The magnitude of the pyroelectric coefficient