4.2: Electromagnetic Radiation

Superposition

The physics of antenna operation is described by Maxwell's equations. Ampere's law, one of Maxwell's equations, was introduced in Section 1.6.1.

\[\overrightarrow{\nabla} \times \overrightarrow{H} = \overrightarrow{J} + \frac{\partial \overrightarrow{D}}{\partial t} \label{4.2.1} \]

In Equation \ref{4.2.1}, \(\overrightarrow{H}\) is the magnetic field intensity in \(\frac{A}{m}\), \(\overrightarrow{D}\) is the displacement flux density in \(\frac{C}{m^2}\), and \(\overrightarrow{J}\) is the current density in \(\frac{A}{m^2}\). In the case of a transmitting antenna, the current density in the antenna comes from a known source, and the electromagnetic field, described by \(\overrightarrow{D}\) and \(\overrightarrow{H}\), can be derived.

Using Maxwell's equations, we can algebraically derive the electromagnetic field only for very simple antennas. The simplest antenna is an infinitesimal dipole antenna, also known as a Hertzian dipole. References [11] derives the electric field intensity, \(\overrightarrow{E}\) in units \(\frac{V}{m}\), for an infinitesimal dipole antenna with length \(dl\) and sinusoidal current \(I_0 \cos(\omega t)\). The result is given in spherical coordinates is

\[\vec{E}= \frac{2 I_{0} \cdot d l \cdot \cos \theta}{4 \pi \epsilon \omega}\left[\frac{\sin \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r^{3}}+\frac{\frac{2 \pi}{\lambda} \cos \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r^{2}}\right] \hat{a}_{r} +\frac{I_{0} \cdot d l \cdot \sin \theta}{4 \pi \epsilon \omega}\left[\frac{\sin \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r^{3}}+\frac{\frac{2 \pi}{\lambda} \cos \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r^{2}}-\frac{\left(\frac{2 \pi}{\lambda}\right)^{2} \sin \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r}\right] \hat{a}_{\theta}. \label{4.2.2} \]

In this expression, \(\omega\) is frequency in \(\frac{rad}{s}\), \(\lambda\) is the wavelength in meters, \(\epsilon\) is the permittivity of the material surrounding the antenna in \(\frac{F}{m}\), and \( (r, \theta, \phi) \) are the coordinates of a point specified in spherical coordinates. For complicated antennas, superposition is used to make the computation feasible. To derive the electromagnetic radiation from a complicated antenna, small straight antenna segments are considered [15, ch. 10]. The electromagnetic radiation from each piece is found, and the principle of superposition is the idea that the radiation from the entire antenna is the sum of these pieces. The same idea applies to linear circuits. If a circuit has a complicated input, the input can be broken up into simpler components. Any voltage in the circuit can be found by finding the contribution due to each of these components then summing.

Reciprocity

Reciprocity is the idea that the behavior of an antenna as a function of angle is the same regardless of whether the antenna is being used to send or receive a signal [15, ch. 10]. A plot of the strength of the field radiated from a transmitter as a function of the angles \(\theta\) and \(\phi\) is called a radiation pattern plot. Similarly, a plot of the strength of the signal received by a receiving antenna as a function of angles \(\theta\) and \(\phi\) assuming a uniform field strength is also called a radiation pattern plot. Consider two identical antennas, one being used as a transmitter and the other as a receiver. The radiation pattern plots will be the same for these two antennas.

Figure \(\PageIndex{1}\): Illustration of power radiating from an isotropic antenna.

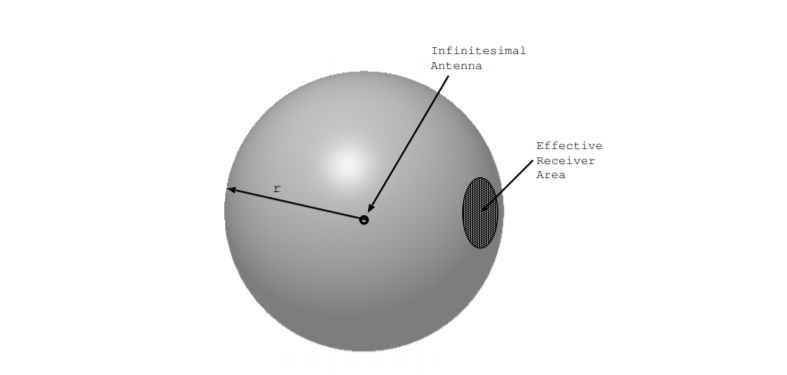
Regardless of the idea of reciprocity, it is often a bad idea to swap the transmitting and the receiving antennas of a system because a transmitter may be designed to handle much more power than a receiver [15, p. 479]. A receiving antenna of effective area \(A\) at a distance \(r\) from an antenna which transmits uniformly in all directions receives at most only the fraction \(\frac{A}{4 \pi r^2}\) of the transmitted power [49, p. 4].

\[P_{rec} = P_{trans} \frac{A}{4 \pi r^2} \nonumber \]

For example, consider an antenna that transmits \(20 kW\) of power uniformly in all directions. Assume a receiving antenna has an effective area of \(10 cm^2\) and covers a portion of a spherical shell as shown in Figure \(\PageIndex{1}\). What is the power received assuming that the antenna is at a distance of \(r = 1 m\), and what is the power received assuming a distance of \(r = 1 km\)?

The surface area intercepted by the receiver is \(10 cm^2 = 10^{-3} m^2\). In the first case, this surface area is the fraction \(\frac{10^{-3}}{4\pi \cdot 1^2}\) of the surface sphere of radius \(1 m\). At most, the antenna can receive this fraction of the power.

\[P = 20 \cdot 10^3 \cdot \frac{10^{-3}}{4\pi \cdot (10^3)^2} = 1.6 \mu W . \nonumber \]

From this example, we can already see some of the advantages and challenges in using electromagnetic waves for communication, and we can see some of the consequences of antenna design. The transmitted power in this example is orders of magnitude larger than the received power. In such a situation, the transmitting circuitry and receiving circuitry will look very different due to the amount of power and current expected during operation. The antennas used will likely also look very different. An antenna transmitting kilowatts of power may need to be mounted on a tower while a receiving antenna that receives milliwatts of power may be built into a portable hand held device.

A typical radio station may want to transmit throughout a city, a radius much larger than 1 km. Furthermore, no energy conversion device is 100% efficient. The electrical power at the receiver 1 m away is therefore going to be less than \(1.6 W\), and the power at the receiver 1 km away is going to be less than \(1.6 \mu W\). Also, all radio receivers are limited by noise. Suppose, for example, that this transmitter is placed at the center of a city of radius 1 km and the receiver can only successfully receive signals with power above \(1 \mu W\) due to \(1 \mu W\) of background noise. A receiver placed 1 km away at the edge of the city may be able to receive the signal successfully, while a receiver further away in the suburbs may not. However, many receivers placed 1 km away with this surface area of \(10 cm^2\) could simultaneously detect the radio signal.

If no building in the city is taller than 10 stories, no receivers are likely to be found at a height over 30 m, for example, above the surface of the earth. However, the transmitter in this example radiates power uniformly in all directions including up. We can design antennas which radiate power in some directions more than others. If we could focus all power from this antenna at altitudes below 30 m, the power at a particular receiver may be larger than we calculated above, so a receiver farther away may be able to detect the signal. The radiation pattern of an antenna is the spatial distribution of the power from the antenna. Radiation pattern plots are discussed further in Sec. 4.4.3.

This example also provides some insights on the safety of working with antennas. The \(10 cm^2\) surface area in this example is, to an order of magnitude, the surface area of a human hand. A typical microwave oven uses less power than the transmitter in this example. Kilowatts of power are enough to cook with, so for this reason, it would be dangerous to touch or even, depending on the frequency, be close to the transmitting antenna. The antenna in this example needs to be mounted on an antenna tower not only for mechanical reasons but also for safety reasons. The amount of power through this surface depends on distance from the transmitter as \(\frac{1}{r^2}\), so the danger level is strongly dependent on distance from the antenna.

Near Field and Far Field

The region within about a wavelength of an antenna is called the near field region. The region beyond multiple wavelengths from an antenna is called the far field or Fraunhofer region. For aperture antennas, instead of wire antennas, distances larger than \(\frac{2(\text{aperture size})^2}{\lambda}\) are considered in the far field [15, p. 498]. The radiation pattern in the near field region and in the far field region are quite different. Near field electromagnetic radiation is used for some specialized applications including tomographic imaging of very small objects [51]. However, receiving antennas used for communication signals almost always operate in the far field region from transmitting antennas. As an example of the difference between near field and far field behavior of an antenna, consider the infinitesimal dipole antenna. The electric field intensity is given in Equation \ref{4.2.2}. The near field electric field from this infinitesimal antenna is found by taking the limit as \(r \rightarrow 0\).

\[\vec{E}=\frac{I_{0} \cdot d l \cdot \cos \theta}{4 \pi \epsilon \omega} \cdot \frac{\sin \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r^{3}}\left(2 \hat{a}_{r}+\hat{a}_{\theta}\right) \nonumber \]

The far field electric field is found by taking the limit as \(r \rightarrow \infty\).

\[\vec{E}=\frac{-I_{0} \omega \cdot d l \cdot \sin \theta}{4 \pi \epsilon} \cdot \frac{\sin \left(\omega t-\frac{2 \pi}{\lambda} r\right)}{r} \hat{a}_{\theta} \nonumber \]

Environmental Effects on Antennas

The electromagnetic radiation from an antenna is affected by the environment surrounding the antenna, specifically nearby large conductors. Sometimes conductors are purposely placed nearby to make an antenna directional. Other times, the conductors, like metal roofs or bridges, just happen to be nearby. If an antenna is placed near a salty lake, the lake surface will reflect the electromagnetic radiation. In other cases, the electrical properties of soil underneath an antenna will affect the electromagnetic radiation [50, ch. 8] [15, p. 635].

Table \(\PageIndex{1}\): Conductivity and relative permittivity of different environments, [50, ch. 8].

Environment	Conductivity \(\sigma\) in \(\frac{1}{\Omega m}\)	Relative permittivity \(\epsilon_r\)
Industrial city	0.001	5
Sand	0.002	10
Rich soil	0.01	14
Fresh water	0.001	80
Salt water	5	80

Numerical simulations are used to understand how an antenna behaves near metal roofs, nearby lakes, or other objects. The effects of the environment are modeled by assigning nearby materials an electrical conductivity \(\sigma\), permittivity \(\epsilon\), and permeability \(\mu\). Often the surroundings have \(\mu \approx \mu_0\), but the other parameters can vary widely. Table \(\PageIndex{1}\) lists values of electrical conductivity and relative permittivity used to model different environments as suggested by reference [50, ch. 8]. The values listed are approximates due to the variety of environments within each category. Additionally, the conductivity can vary from day to day. For example, electromagnetic waves may interact with farmland very differently on a snowy winter day, after a spring rainfall, and during a dry spell in summer. Also, even for a single uniform material, conductivity and permittivity are functions of frequency.