1.6: Problems
- Page ID
- 49282
Section 1-1
1. Find the area of a circle in the \(xy\) plane centered at the origin using:
(a) rectangular coordinates \(x + y^{2} = a^{2}\) (Hint:
\(\int \sqrt{a^{2} - x^{2}} dz = \frac{1}{2} [x \sqrt{a^{2} - x^{2}} + a^{2} \sin^{-1} (x /a)]\) )
(b) cylindrical coordinates \(\textrm{r}=a\).
Which coordinate system is easier to use?
2. Find the volume of a sphere of radius \(R\) centered at the origin using:
(a) rectangular coordinates \(x^{2} + y + z^{2} = R^{2}\) (Hint:
\(\int \sqrt{a^{2}-x^{2}}dx=\frac{1}{2}\left [x\sqrt{a^{2}-x^{2}}+a^{2}\sin ^{-1}\left ( x/a \right ) \right ]\))
(b) cylindrical coordinates \(r^{2} + z^{2} = R^{2}\);
(c) spherical coordinates \(r=\textbf{R}\)
Which coordinate system is easiest?
Section 1-2
Given the three vectors
\(\textbf{A} = 3 \textbf{i}_{x} + 2 \textbf{i}_{y} - \textbf{i}_{z} \\ \textbf{B} = 3 \textbf{i}_{x} - 4 \textbf{i}_{y} - 5 \textbf{i}_{z} \\ \textbf{C} = \textbf{i}_{x} - \textbf{i}_{y} + \textbf{i}_{z}\)
find the following:
(a) \(\textbf{A}\pm \textbf{B},\textbf{B}\pm \textbf{C},\textbf{A}\pm \textbf{C}\)
(b) \(\textbf{A}\cdot \textbf{B},\textbf{B}\cdot \textbf{C},\textbf{A}\cdot \textbf{C}\)
(c) \(\textbf{A}\times \textbf{B},\textbf{B}\times \textbf{C},\textbf{A}\times \textbf{C}\)
(d) \(\left (\textbf{A}\times \textbf{B} \right )\cdot \textbf{C},\textbf{A}\cdot \left (\textbf{B}\times \textbf{C} \right )\) [Are they equal?]
(e) \(\textbf{A}\times \left (\textbf{B} \times \textbf{C} \right ),\textbf{B}\left ( \textbf{A}\cdot \textbf{C} \right )-\textbf{C}\left ( \textbf{A}\cdot \textbf{B} \right )\) [Are they equal?]
(f) What is the angle between \(\textbf{A}\) and \(\textbf{C}\) and between \(\textbf{B}\) and \(\textbf{A}\times\textbf{C}\)?
Given the sum and difference between two vectors,
\(\textbf{A} + \textbf{B} = -\textbf{i}_{x} + 5 \textbf{i}_{y} - 4 \textbf{i}_{z} \\ \textbf{A} - \textbf{B} = 3 \textbf{i}_{x} - \textbf{i}_{y} - 2 \textbf{i}_{z}\)
find the individual vectors \(\textbf{A}\) and \(\textbf{B}\).
(a) Given two vectors \(\textbf{A}\) and \(\textbf{B}\), show that the component of \(\textbf{B}\) parallel to \(\textbf{A}\) is
\(\textbf{B}_{\parallel} = \frac{\textbf{B} \cdot \textbf{A}}{\textbf{A} \cdot \textbf{A}} \textbf{A}\)
(Hint: \(\textbf{B}_{\parallel} = \alpha \textbf{A}\). What is \(\alpha\)?)
(b) if the vectors are
\(\textbf{A}=\textbf{i}_{x}-2\textbf{i}_{y}+\textbf{i}_{z}\\
\textbf{B}=3\textbf{i}_{x}-5\textbf{i}_{y}-5\textbf{i}_{z}\)
what are the components of \(\textbf{B}\) parallel and perpendicular to \(\textbf{A}\)?
\(\textbf{B} = \textbf{B}_{\perp} + \textbf{B}_{\parallel}\)
What are the angles between each of the following vectors:
\(\textbf{A} = 4 \textbf{i}_{x} - 2 \textbf{i}_{y} + 2 \textbf{i}_{z} \\ \textbf{B} = -6 \textbf{i}_{x} + 3 \textbf{i}_{y} - 3 \textbf{i}_{z} \\ \textbf{C} = \textbf{i}_{x} + 3 \textbf{i}_{y} + \textbf{i}_{z}\)
Given the two vectors
\(\textbf{A} = 3 \textbf{i}_{x} + 4 \textbf{i}_{y} \textrm{ and } \textbf{B} = 7 \textbf{i}_{x} - 24 \textbf{i}_{y}\)
(a) What is their dot product?
(b) What is their cross product?
(c) What is the angle \(\theta\) between the two vectors?
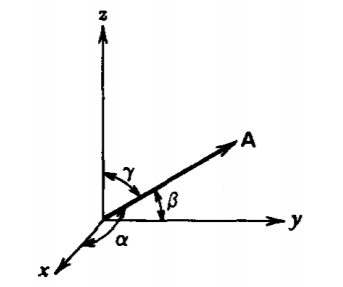
Given the vector
\(\textbf{A} = \textbf{A}_{x}\textbf{i}_{x} + A_{y}\textbf{i}_{y} + A_{z}\textbf{i}_{z}\)
the directional cosines are defined as the cosines of the angles between \(\) and each of the Cartesian coordinate axes. Find each of these directional cosines and show that
\(\cos^{2} \alpha + \cos^{2} \beta + \cos^{2} \gamma = 1\)
A triangle is formed by the three vectors \(\textbf{A}\), \(\textbf{B}\), and \(\textbf{C}=\textbf{B}-\textbf{A}\).
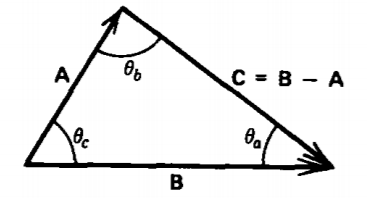
(a) Find the length of the vector \(\textbf{C}\) in terms of the lengths of \(\textbf{A}\) and \(\textbf{B}\) and the enclosed angle \(\theta_{c}\). The result is known as the law of cosines. (Hint: \(\textbf{C}\cdot \textbf{C}=\left ( \textbf{B}-\textbf{A} \right )\cdot \left ( \textbf{B}-\textbf{A} \right )\).)
(b) For the same triangle, prove the law of sines:
\(\frac{\sin \: \theta_{a}}{A} = \frac{\sin \: \theta_{b}}{B} = \frac{\sin \: \theta_{c}}{C}\)
(Hint: \(\textbf{B}\times \textbf{A}=\left ( \textbf{C}+\textbf{A} \right )\times \textbf{A}\).)
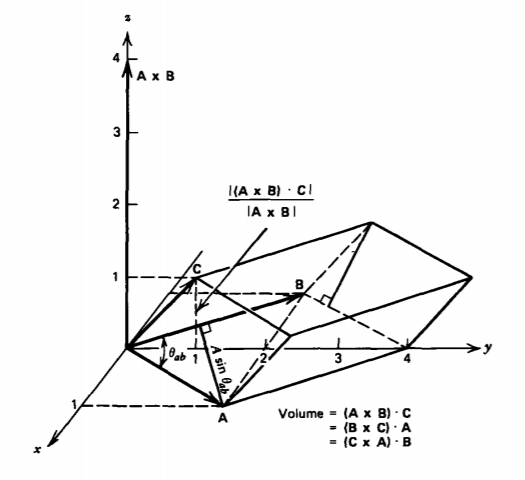
(a) Prove that the dot and cross can be interchanged in the scalar triple product
\(\left (\textbf{A}\times \textbf{B} \right )\cdot \textbf{C}=\left ( \textbf{B}\times \textbf{C} \right )\cdot \textbf{A}=\left ( \textbf{C}\times \textbf{A}\right )\cdot \textbf{B}\)
(b) Show that this product gives the volume of a parallelepiped whose base is defined by the vectors \(\) and \(\) and whose height is given by \(\).
(c) If
\(\textbf{A} = \textbf{i}_{x} + 2 \textbf{i}_{y}, \: \: \: \textbf{B} = - \textbf{i}_{x} + 2 \textbf{i}_{y}, \: \: \: \textbf{C} = \textbf{i}_{x} + \textbf{i}_{z}\)
verify the identities of (a) and find the volume of the parallelepiped formed by the vectors.
(d) Prove the vector triple product identity
\(\textbf{A}\times \left (\textbf{B}\times \textbf{C} \right )=\textbf{B}\left (\textbf{A}\cdot \textbf{C} \right )-\textbf{C}\left (\textbf{A}\cdot \textbf{B} \right )\)
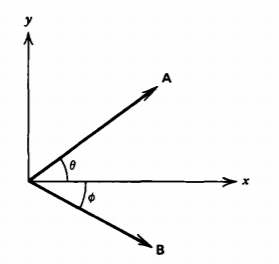
(a) Write the vectors \(\textbf{A}\) and \(\textbf{B}\) using Cartesian coordinates in terms of their angles \(\theta\) and \(\phi\) from the \(x\) axis.
(b) Using the results of (a) derive the trigonometric expansions
\(\sin(\theta + \phi) = \sin \: \theta \: \cos \: \phi + \sin \: \phi \: \cos \: \theta\)
\(\cos (\theta + \phi) = \cos \: \theta \: \cos \: \phi - \sin \: \theta \: \sin \: \phi\)
Section 1-3
Find the gradient of each of the following functions where \(a\) and \(b\) are constants:
(a) \(f = axz + bx^{3}y\)
(b) \(f = (a/\textrm{r}) \: \sin \: \phi + b \textrm{r} z^{2} \: \cos \: 3 \phi\)
(c) \(f = ar \: \cos \: \theta + (b/r^{2}) \: \sin \: \phi\)
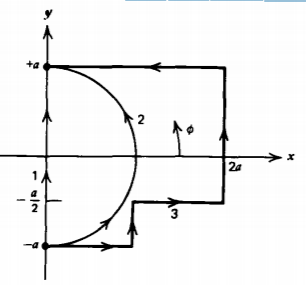
Evaluate the line integral of the gradient of the function
\(f = r \: \sin \: \phi\)
over each of the contours shown.
Section 1-4
Find the divergence of the following vectors:
(a) \(\textbf{A} = x \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z} = r \textbf{i}_{r}\)
(b) \(\textbf{A} = (xy^{2}z^{3})[\textbf{i}_{x} + \textbf{i}_{y} + \textbf{i}_{z}]\)
(c) \(\textbf{A} = \textrm{r} \: \cos \: \phi \textbf{i}_{\textrm{r}} + [(z/\textrm{r}) \: \sin \: \phi)] \textbf{i}_{z}\)
(d) \(\textbf{A} = r^{2} \: \sin \: \theta \: \cos \: \phi \: [\textbf{i}_{r} + \textbf{i}_{\theta} + \textbf{i}_{\phi}]\)
Using the divergence theorem prove the following integral identities:
(a) \(int_{V} \nabla f d V = \oint_{S} f \: \textbf{dS}\)
(Hint: Let \(\textbf{A}=\textbf{i}f\), where \(\textbf{i}\) is any constant unit vector.)
(b) \(\int_{V} \nabla \times \textbf{F} \: d \textrm{V} = -\oint_{S} \textbf{F} \times \textbf{dS}\)
(Hint: Let \(\textbf{A}=\textbf{i}\times \textbf{F}\).)
(c) Using the results of (a) show that the normal vector integrated over a surface is zero:
\(\oint_{S} \textbf{dS} = 0\)
(d) Verify (c) for the case of a sphere of radius \(R\).
(Hint: \(\textbf{i}_{r} = \sin \: \theta \: \cos \: \phi \textbf{i}_{x} + \sin \: \theta \: \sin \: \phi \textbf{i}_{y} + \cos \: \theta \textbf{i}_{z}\))
Using the divergence theorem prove Green's theorem
\(\oint_{S}[f \nabla g - g \nabla f] \cdot \textbf{dS} = \int_{V} [f \nabla^{2} g - g \nabla^{2} f] dV\)
(Hint: \(\nabla \cdot (f \nabla g) = f \nabla^{2} g + \nabla f \cdot \nabla g.\) )
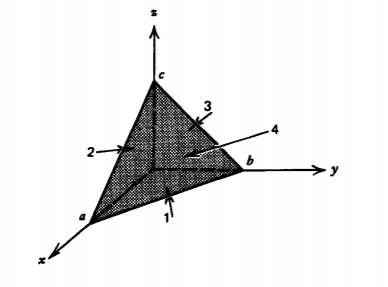
(a) Find the area element \(\textbf{dS} \) (magnitude and direction) on each of the four surfaces of the pyramidal figure shown.
(b) Find the flux of the vector
\(\textbf{A} = r \textbf{i}_{r} = x \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z}\)
through the surface of (a).
(c) Verify the divergence theorem by also evaluating the flux as
\(\Phi = \int_{V} \nabla \cdot \textbf{A} dV\)
Section 1-5
Find the curl of the following vectors:
(a) \(\textbf{A} = x^{2} y \textbf{i}_{x} + y^{2} z \textbf{i}_{y} + x y \textbf{i}_{z}\)
(b) \(\textbf{A} = \textrm{r} \: \cos \: \phi \textbf{i}_{z} + \frac{z \: \sin \: \phi}{\textrm{r}} \textbf{i}_{\textrm{r}}\)
(c) \(\textbf{A} = r^{2} \sin \: \theta \: \cos \: \phi \: \textbf{i}_{r} + \frac{\cos \: \theta \: \sin \: \phi}{r^{2}} \textbf{i}_{\theta}\)
Using Stokes' theorem prove that
\(\oint_{L} f \: \textbf{dl} = - \int_{S} \nabla f \times \textbf{dS}\)
(Hint: Let \(\textbf{A}=\textbf{i}f\), where \(\textbf{i}\) is any constant unit vector.)
Verify Stokes' theorem for the rectangular bounding contour in the \(xy\) plane with a vector field
\(\textbf{A} = (x + a)(y + b)(z + c) \textbf{i}_{x}\)
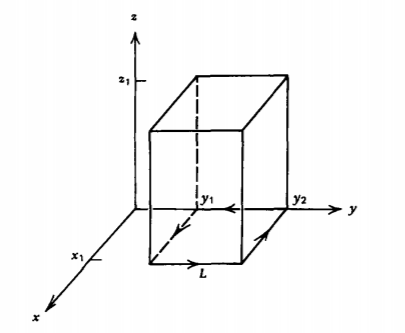
Check the result for (a) a flat rectangular surface in the \(xy\) plane, and (b) for the rectangular cylinder.
Show that the order of differentiation for the mixed second derivative
\(\frac{\partial}{\partial x} (\frac{\partial f}{\partial y}) = \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})\)
does not matter for the function
\(f = \frac{x^{2} \ln \: y}{y}\)
Some of the unit vectors in cylindrical and spherical coordinates change direction in space and thus, unlike Cartesian unit vectors, are not constant vectors. This means that spatial derivatives of these unit vectors are generally nonzero. Find the divergence and curl of all the unit vectors.
A general right-handed orthogonal curvilinear coordinate system is described by variables \(\left ( u,v,w \right )\), where
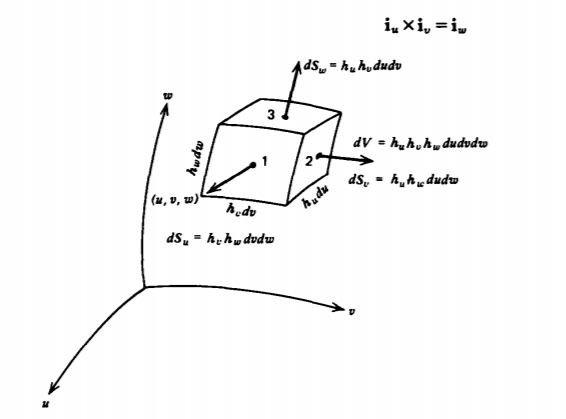
Since the incremental coordinate quantities \(du\), \(dv\), and \(dw\) do not necessarily have units of length, the differential length elements must be multiplied by coefficients that generally are a function of \(u\), \(v\), and \(w\):
\(dL_{u} = h_{u}du, \: \: dL_{v} = h_{v}dv, \: \: dL_{w} = h_{w}dw\)
(a) What are the \(h\) coefficients for the Cartesian, cylindrical, and spherical coordinate systems?
(b) What is the gradient of any function \(f\left ( u,v,w \right )\)?
(c) What is the area of each surface and the volume of a differential size volume element in the \(\left ( u,v,w \right )\) space?
(d) What are the curl and divergence of the vector
\(\textbf{A} = A_{u}\textbf{i}_{u} + A_{v}\textbf{i}_{v} + A_{w} \textbf{i}_{w}\)?
(e) What is the scalar Laplacian \(\nabla^{2} f = \nabla \cdot (\nabla f)\)?
(f) Check your results of (b)-(e) for the three basic coordinate systems.
Prove the following vector identities:
(a) \(\nabla(fg) = f \nabla g + g \nabla f\)
(b) \(\nabla(\textbf{A} \cdot \textbf{B}) = (\textbf{A} \cdot \nabla) \textbf{B} + (\textbf{B} \cdot \nabla) \textbf{A} + \textbf{A} \times (\nabla \times \textbf{B}) + \textbf{B} \times (\nabla \times \textbf{A})\)
(c) \(\nabla \cdot (f \textbf{A}) = f \nabla \cdot \textbf{A} + (\textbf{A} \cdot \nabla ) \)
(d) \(\nabla \cdot (\textbf{A} \cdot \textbf{B}) = \textbf{B} \cdot (\nabla \times \textbf{A}) - \textbf{A} \cdot (\nabla \times \textbf{B})\)
(e) \(\nabla \times (\textbf{A} \times \textbf{B}) = \textbf{A}(\nabla \cdot \textbf{B}) - \textbf{B}(\nabla \cdot \textbf{A}) + (\textbf{B} \cdot \nabla) \textbf{A} - (\textbf{A} \cdot \nabla) \textbf{B}\)
(f) \(\nabla \times (f \textbf{A}) = \nabla f \times \textbf{A} + f \nabla \times \textbf{A}\)
(g) \(\nabla \times \textbf{A}) \times \textbf{A} = (\textbf{A} \cdot \nabla) \textbf{A} - \frac{1}{2} \nabla (\textbf{A} \cdot \textbf{A})\)
(h) \(\nabla \times (\nabla \times \textbf{A}) = \nabla (\nabla \cdot \textbf{A}) - \nabla^{2} \textbf{A}\)
Two points have Cartesian coordinates \((1, 2, -1)\) and \((2, -3, 1)\).
(a) What is the distance between these two points?
(b) What is the unit vector along the line joining the two points?
(c) Find a unit vector in the \(xy\) plane perpendicular to the unit vector found in (b).
Miscellaneous
A series RLC circuit offers a good review in solving linear, constant coefficient ordinary differential equations. A step voltage \(V_0\) is applied to the initially unexcited circuit at \(t =0\).
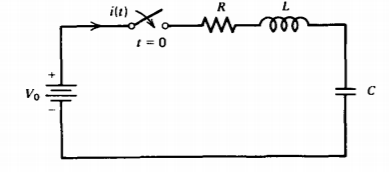
(a) Write a single differential equation for the current.
(b) Guess an exponential solution of the form
\(i(t) = \hat{I}e^{st}\)
and find the natural frequencies of the circuit.
(c) What are the initial conditions? What are the steady state voltages across each element?
(d) Write and sketch the solution for \(i\left ( t \right )\) when
\((\frac{R}{2L})^{2} < \frac{1}{LC'} \: (\frac{R}{2L})^{2} = \frac{1}{LC'} \: (\frac{R}{2L})^{2} \> \frac{1}{LC}\)
(e) What is the voltage across each element?
(f) After the circuit has reached the steady state, the terminal voltage is instantly short circuited. What is the short circuit current?
Many times in this text we consider systems composed of repetitive sequences of a basic building block. Such discrete element systems are described by difference equations. Consider a distributed series inductance-shunt capacitance system excited by a sinusoidal frequency \(\omega\) so that the voltage and current in the \(n\)th loop vary as
\(i_{n} = \textrm{Re} (I_{n}e^{j \omega t}); \: \: v_{n} = \textrm{Re}(V_{n} e^{j \omega t})\)
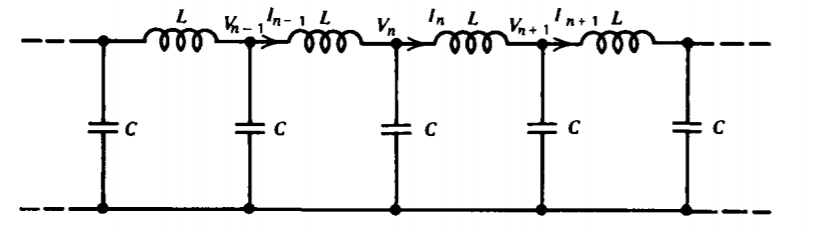
(a) By writing Kirchoff's voltage law for the \(\)nth loop, show that the current obeys the difference equation
\(I_{n + 1} - (2 = \frac{\omega^{2}}{\omega_{0}^{2}}) I_{n} + I_{n-1} = 0\)
What is \(\omega_{o}^{2}\)?
(b) Just as exponential solutions satisfy linear constant coefficient differential equations, power-law solutions satisfy linear constant coefficient difference equations
\(I_{n} = \hat{I} \lambda^{n}\)
What values of \(\lambda\) satisfy (a)?
(c) The general solution to (a) is a linear combination of all the possible solutions. The circuit ladder that has \(N\) nodes is excited in the zeroth loop by a current source
\(i_{0} = \textrm{Re}(I_{0}e^{j \omega t}\)
Find the general expression for current \(i_{n}\) and voltage \(v_{n}\) for any loop when the last loop \(N\) is either open (\(I_{N} = 0\)) or short circuited (\(V_{N} = 0\)). (Hint: \(a + \sqrt{a^{2} - 1} = 1/(a = \sqrt{a^{2} -1})\)
(d) What are the natural frequencies of the system when the last loop is either open or short circuited?
(Hint: \((1)^{1/(2N)} = e^{j 2 \pi r/2N}, \: \: r = 1, 2, 3, ...., 2N.)\)