2.5: Power and Efficiency
- Page ID
- 25095
The terms power and energy are often used incorrectly as synonyms. Although related, they are not the same thing. As already mentioned, energy is the ability to do work. In contrast, power is the rate of energy usage. Power is denoted by the letter \(P\) and has units of watts, although other units are sometimes used such as the horsepower (1 horsepower \(\approx\) 746 watts). One watt is defined as one joule of energy consumed per second.
\[1 \text{ watt } \equiv 1 \text{ joule } / 1 \text{ second } \label{2.5} \]
As a formula,
\[P = W / t \label{2.6} \]
Where
\(P\) is the power in watts,
\(W\) is the energy in joules,
\(t\) is the time in seconds.
To better understand the concept, consider for a moment a delicious peanut butter and banana sandwich. This sandwich contains a certain number of food calories, let's say 300 in total. A food calorie refers to a certain amount of energy that humans can extract from an item of food. That energy enables us to do some manner of work such as walking, swimming or just breathing. The sandwich can be seen as an energy storage medium, a battery for biological units called humans. The question is, what do we do with the energy, and more to the point, how fast do we use it? For example, that sandwich might be sufficient to allow someone to run a 5k (3.1 mile) road race in 17 minutes. In contrast, it also might be sufficient to allow that same person to watch television for three hours. It's the same amount of energy being used, it's just being used at a much faster rate in the former case. That rate is power. The 5k runner has a much higher power output than the TV watcher.
100 joules are consumed by a device in 0.1 seconds. Determine the power in watts and in horsepower.
\[P = \frac{W}{t} \nonumber \]
\[P = \frac{100 J}{0.1s} \nonumber \]
\[P = 1000 W \nonumber \]
As one horsepower is approximately 746 watts, this is equivalent to
\[P_{hp} = \frac{P_W}{746W/hp} \nonumber \]
\[P_{hp} = \frac{1000 W}{746W/hp} \nonumber \]
\[P_{hp} = 1.34 hp \nonumber \]
Power can also be found by multiplying a current by the associated voltage. To begin, we note the definitions of current and voltage, Equations 2.3.2 and 2.4.2 respectively, and then combine them.
\[I = \frac{Q}{t} \nonumber \]
\[V = \frac{W}{Q} \nonumber \]
\[I \times V = \frac{Q}{t} \times \frac{W}{Q} = \frac{W}{t} \nonumber \]
From Equation \ref{2.6}, we know that \(P = W/t\), thus \(P = IV\). This is known as power law.
\[P = I \times V \label{2.7} \]
Where
\(P\) is the power in watts,
\(I\) is the current in amps,
\(V\) is the voltage in volts.
If a 9 volt battery delivers a current of 0.1 amps, determine the power delivered in watts.
\[P = I \times V \nonumber \]
\[P = 0.1amps \times 9volts \nonumber \]
\[P = 0.9W \nonumber \]
Efficiency
Efficiency is the ratio of useful output power to applied power expressed as a percentage. It is denoted by the Greek letter \(\eta\) (eta) and is always less than 100%. Expressed as a formula,
\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \label{2.8} \]
Where
\(\eta\) is the efficiency in percent,
\(P_{out}\) is the output power,
\(P_{in}\) is the input power.
Generally speaking, the higher the efficiency, the better. This implies less waste. In other words, if a system is 30% efficient, then 70% of the input power is wasted, whereas if a system is 99% efficient, then only 1% of the input power is wasted. The concept is illustrated graphically in Figure 2.5.1 . In most systems, waste power turns into heat which is not a desired commodity, and in fact often reduces the lifespan of electrical components.
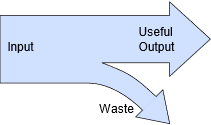
Figure 2.5.1 : Basic concept of efficiency.
If a device draws 200 watts of power and has a useful output of 120 watts, determine the efficiency.
\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \nonumber \]
\[\eta = \frac{120W}{200W} \times 100 \% \nonumber \]
\[\eta = 60 \% \nonumber \]
In this case, the device is wasting 40% of the input power, or 80 watts.
An audio amplifier has a maximum rated output of 100 watts to a loudspeaker. If it exhibits an efficiency of 70%, determine the input power required and the amount of power wasted.
\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \nonumber \]
\[P_{in} = \frac{P_{out}}{\eta} \times 100 \% \nonumber \]
\[P_{in} = \frac{100W}{70 \%} \times 100 \% \nonumber \]
\[P_{in} = 142.9 watts \nonumber \]
As 142.9 watts are drawn by the amplifier and only 100 watts are delivered to the loudspeaker, then the difference, or 42.9 watts, is wasted power (most likely just making the amplifier hot).