6.23: Problems
- Page ID
- 52412
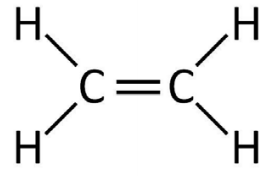
1. Consider the interaction of two carbon atoms each with one electron in a frontier \(2p_{z}\) atomic orbital. Assuming the positions of the atoms are fixed, the Hamiltonian of the system consists of a kinetic energy operator, and two Coulombic potential terms: one for the central atom and one for its neighbor:
\( H=T+V_{1}+V_{2} \)
Assume the wavefunction in this two atom system can be written as
\( \psi = c_{1}\phi_{1}+c_{2}\phi_{2} \)
where \(\phi_{1}\) and \(\phi_{2}\) are the \(2p_{z}\) atomic orbitals on the first and second carbon atoms, respectively, and \(c_{1}\) and \(c_{2}\) are constants.
The self energy is defined as
\( \alpha_{r} = \left< \phi_{r}| T+V_{r} |\phi_{r} \right> \)
The hopping interactions are defined as
\( \beta_{sr} = \left< \phi_{s}| V_{s} |\phi_{r} \right> \)
Earlier, we assumed that the overlap integral between frontier orbitals on atomic sites s and r could be approximated as
\( S_{sr} = \left< \phi_{s}|\phi_{r} \right> = \delta_{sr} \)
Do not make that assumption here and show that the electron energies of the system satisfy
\[ \det (H - ES) = 0 \nonumber \]
where H is a 2×2 Hamiltonian matrix and S is a 2×2 overlap matrix and E is a constant.
(a) Write each matrix in Equation (6.24.1) in terms of the self energies, hopping integrals and overlap integrals.
(b) Under what conditions can you safely ignore the overlap integrals?
2.
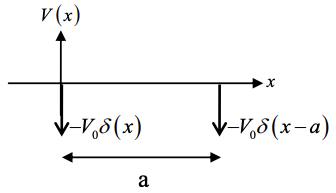
(a) Consider the potential \(V(x) = -V_{0}\delta(x)\), sketched below.

(i) Show that the wavefunction is given by \(\phi_{1}(x) = \sqrt{k}e^{-k|x|}\) where \(k = \frac{mV_{0}}{\hbar^{2}}\)
(ii) Show that the energy of the bound states (E<0) is \(E_{1} = -\frac{mV_{0}^{2}}{2\hbar^{2}}\).
(b) Now add a second delta function potential at x = a.
i.e. if the previous Hamiltonian was \(H_{1} = -\frac{\hbar^{2}}{2m} \frac{d^{2}}{dx^{2}}-V_{0}\delta(x)\), the new Hamiltonian is \(H = H_{1}+V\) where \(V = -V_{0}\delta(x-a)\)
Let the wavefunction of the new system be approximated by \(\psi=c_{1}\phi_{1}+c_{2}\phi_{2}\) where \(\phi_{2} = \phi_{1}(x-a)\) and \(c_{1}\) and \(c_{2}\) are constants.
The self energy is \(\alpha = \left< \phi_{1}|H_{1}|\phi_{1} \right>\)
The hopping interaction is \(\beta = \left< \phi_{2}|V|\phi_{1} \right>\)
In addition, define the overlap integral \(S = \left< \phi_{1}|\phi_{2} \right>\), and \(\gamma = \left< \phi_{1}|V|\phi_{1} \right>\)
By evaluating the expressions
\( \left< \phi_{1} |H| \psi \right> = E \left< \phi_{1}|\psi \right> \)
and
\( \left< \phi_{2} |H| \psi \right> = E \left< \phi_{2}|\psi \right> \)
show that
\( \left(\begin{array}{cc}
\alpha+\gamma & \alpha S+\beta \\
\alpha S+\beta & \alpha+\gamma
\end{array}\right)\left(\begin{array}{l}
c_{1} \\
c_{2}
\end{array}\right)=E\left(\begin{array}{cc}
1 & S \\
S & 1
\end{array}\right)\left(\begin{array}{l}
c_{1} \\
c_{2}
\end{array}\right) \)
Now show that \(\alpha = \frac{-mV_{0}^{2}}{2\hbar},\ \beta = \frac{-mV_{0}^{2}}{\hbar^{2}}e^{-ka},\ S(1+ka)e^{-ka}, \text{ and } \gamma=\frac{-mV_{0}^{2}}{\hbar^{2}}e^{-2ka}\)
Dropping terms containing \(e^{-2ka}\), show that the matrix reduces to \(E \approx \alpha \pm \beta\)
3. For molecules where each carbon atom contributes at least one delocalized electron to a \(\pi\) orbital, we can use the perimeter free electron orbital theory approximation, which is described below.
Assume that the molecule in question is a circular ring of atoms and assume an infinite square well potential.
(a) Show that the energy levels of a molecule under this approximation are
\( E = \frac{h^{2}m_{l}^{2}}{2m_{e}L^{2}} \)
where where \(m_{l}\) is an integer, and L is the perimeter of the molecule.
Hint: The Hamiltonian in polar coordinates is given by:
\( \hat{H} = \frac{\hbar^{2}}{2m_{e}}\left( \frac{d^{2}}{dr^{2}}+\frac{1}{r}\frac{d}{dr}+\frac{1}{r^{2}}\frac{d^{2}}{d\phi^{2}} \right) \)
(b) According to the perimeter free electron orbital theory approximation, the energy level structure of anthracene is shown in Figure 6.24.3, below.
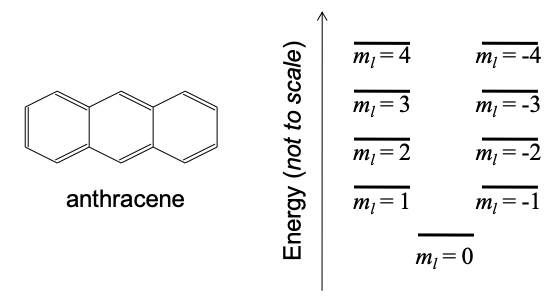
(i) Why is there a solution for \(m_{l} = 0\) in anthracene but no solution for n = 0 in the infinite quantum well?
(ii) Why are there solutions for negative \(m_{l}\) in anthracene but no solutions for negative n in the infinite quantum well? Hint: consider the Pauli exclusion principle.
(c) Calculate the molecular orbitals and HOMO-LUMO gap of anthracene. Take a = 1.38Å as the C-C bond length. Assume each C atom donates 1 electron to the frontier orbitals.
4. Consider the periodic molecule consisting of two different alternating atom types illustrated below (frontier orbitals are shown).

(a) How many atoms are in the unit cell in this molecule? Using periodic boundary conditions and assuming molecular wavefunctions of the Bloch form, find the energy levels.
(b) Find the density of states.
5. The band structure of molecular crystals
Let \(\phi({\bf{r}})\) be the HOMO of a typical molecule. As in most stable molecules, \(\phi({\bf{r}})\) is fully occupied and contains two electrons.
Unlike conventional crystalline semiconductors such as Si, the unit cells in a molecular crystal are held together by weak van der Waals forces. A typical value for the interaction between nearest neighbors in a van der Waals bonded solid is
\( \beta=\left< \phi({\bf{r+R}})|H| \phi({\bf{r}})\right> \approx -10\ meV \)
where H is the Hamiltonian for the interaction between nearest neighbors and R is the set of lattice vectors connecting the molecule at r to its nearest neighbors.
(a) Calculate the "valence" band structure of a cubic molecular crystal of this molecule. Let \(\left<\phi({\bf{r}})|H| \phi({\bf{r}})\right> = \alpha\). (See Figure 6.24.5 below).
(b) Show that all molecular crystals with filled HOMOs are insulators.
6. Consider the following polymer:

Assume the spacing between atoms on the linear backbone is \(a_{0}\), as shown. Also, assume all atoms are the same element, \(\beta_{1}\) and \(\beta_{2}\) are the hopping interactions between atoms as shown, the self energy at each atom is \(\alpha\), and assume each atom contributes one electron.
(a) What is the primitive unit cell and primitive lattice vector?
(b) Show that the dispersion relation is given by
\( E = \alpha +\beta_{2}\ cos(ka_{0}) \pm \sqrt{\beta_{2}^{2}\ cos^{2}(ka_{0})+2\beta_{1}^{2}(1+cos(ka_{0}))} \)
(c) Is the polymer metallic or insulating?
7. Graphene and carbon nanotube transistors
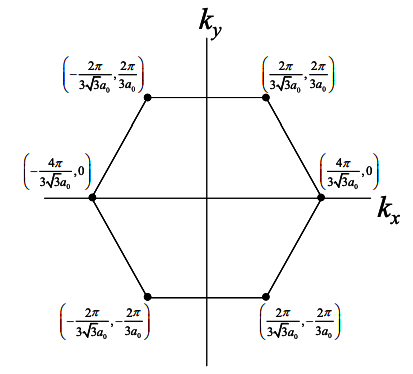
(a) With reference to the bandstructure of graphene shown below, explain why graphene when rolled up into nanotubes can be either metallic or semiconducting?
(b) Using the k-space plot shown below, determine whether the following (n,m) nanotubes are metallic or semiconducting. Recall that nanotubes are rolled-up graphene sheets with wrapping vector \(\bar{w}=na_{1}+ ma_{2}=(n,m)\).
i) (0,6)
ii) (N,N)
iii) (3,9)
iv) (3,5)
(c) At present, there is much interest in using graphene (as opposed to carbon nanotubes) as the channel material for field effect transistors. The idea is to fabricate entire chips on a single sheet of graphene.
First the graphene is deposited somehow (this is a technological challenge at present). Next, the graphene is cut up. Finally, contacts and gate insulators are deposited.
Why is the graphene cut up? Explain with reference to particle in a box models of conductors.
8. Carbon Nanotubes
(a) Prove the identities in Equation (6.21.3) and Equation (6.21.4).
(b) Derive Equation (6.21.6) from Equation (6.21.5).
9. This question relates to the molecule shown below.
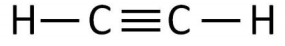
a) Write the Hamiltonian matrix for this molecule in terms of the tight binding parameters \(\alpha\), and \(\beta\).
b) Write the energy for this molecular orbital in terms of \(\alpha\) and \(\beta\).
c) Compare the density of states of the HOMO and LUMO of the previous molecule to the one below.