5.5: Offsets
- Page ID
- 3576
Offsets are undesirable DC levels appearing at the output of a circuit. If op amps were perfect, there would be no such thing as an offset. Even though part matching is very close when ICs are made, the parts will not be identical. One possible example is the fact that the transistors used for the differential amplifier stage will not have identical characteristics. Because of this, their DC bias points are slightly different. This difference, or unbalance, is amplified by the remaining stages and will eventually produce a DC voltage at the output. Because all op amps are slightly different, you never know what the exact output offset will be. For measurement applications, this offset creates uncertainty in readings. For example, if the circuit output measures 100 mV, the signal might be 99 mV with 1 mV of offset. It might also be 101 mV with -1mV offset. In other applications, offsets can harm following stages or loads. Dynamic loudspeakers and headphones are two loads that should not be fed DC signals. This will reduce their maximum volume and increase their distortion. In short, offsets are not desired. Let's see what the causes are and how we can reduce or eliminate their effect.
5.5.1: Offset Sources and Compensation
For bipolar input sections the major cause of input current mismatch is the variation of beta. Base-emitter junction voltage variation is the major cause of input voltage deviation. For field effect devices, current variation is much less of a problem as the magnitude of input current is very low to begin with. Unfortunately, FETs do suffer from larger input voltage variations due to transconductance curve mismatches.
As mentioned in Chapter Two, the input current into the bases (or gates, in the case of an FET) of the first stage is called \(I_B\), the input bias current. In reality, this is an average of the two input currents, \(I_{B+}\) and \(I_{B-}\). The magnitude of their difference is called the input offset current, \(I_{OS}\) (some manufacturers use the symbol \(I_{IO}\)). Note that the actual direction of \(I_B\) is normally not specified, but can usually be determined from the manufacturer's circuit diagram. \(I_B\) flows into the op amp if the input devices are NPN, and out of the op amp if the input devices are PNP.
\[ I_B = \frac{I_{B+} + I_{B-}}{2} \nonumber \]
\[ I_{OS} = | I_{B+} − I_{B-} | \label{5.12} \]
The voltage difference for the input stage is referred to as the input offset voltage, \(V_{OS}\) (some manufacturers use the symbol \(V_{IO}\)). This is the potential required between the two inputs to null the output, that is, to re-align the output to 0 V DC. Both \(I_{OS}\) and \(V_{OS}\) are available on data sheets. The absolute magnitude of these offsets generally gets worse at temperature extremes. Table \(\PageIndex{1}\) shows some typical values. Note the low \(I_{B}\) and \(I_{OS}\) values for the FET input 411.
| Device | \(I_B\) | \(I_{OS}\) | \(V_{OS}\) |
| 5534 | 800 nA | 10 nA | 0.5 mV |
| 411 | 50 pA | 25 pA | 0.8 mV |
| 318 | 150 nA | 30 nA | 4 mV |
| 741 | 80 nA | 20 nA | 1 mV |
Table \(\PageIndex{1}\)
Remember, these numbers are absolutes, so when \(I_{OS}\) is specified as 10 nA, it means that the actual \(I_{OS}\) can be anywhere between -10 nA and +10 nA. \(I_B\), \(I_{OS}\) and \(V_{OS}\) combine with other circuit elements to produce an output offset voltage. As this is a linear circuit, superposition may be used to separately calculate their effects. The model in Figure \(\PageIndex{1}\) will be used. \(R_i\) and \(R_f\) are the standard feedback components, and \(R_{off}\) is called the offset compensation resistor (in some cases it may be zero). Because the input signal is grounded, this model is valid for both inverting and noninverting amplifiers.
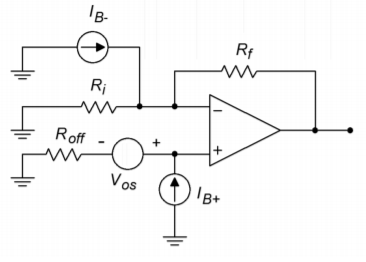
Figure \(\PageIndex{1}\): Offset model.
\(V_{OS}\) is seen as a small input voltage and is multiplied by the circuit's noise gain in order to find its contribution to the output offset. Offsets are by nature DC, so it is important to use the DC noise gain. Consequently, any capacitors found within the feedback loop should be mathematically “opened” for this calculation (for example, when working with the filter circuits presented in Chapter Eleven)
\[ V_{out−offset 1} = A_{noise} V_{OS} \label{5.13} \]
where
\[ A_{noise} = 1+ \frac{R_f}{R_i} = \frac{R_i+R_f}{R_i} \nonumber \]
\(I_B\) and \(I_{OS}\) pass through input and feedback resistors to produce their output contributions. First, consider the effect of \(I_{B+}\). This creates a voltage across \(R_{off}\). This voltage is then multiplied by the circuit noise gain to yield its portion of the output offset.
\[ V_{out -offset 2} = I_{B+} R_{off} A_{noise} \label{5.14} \]
For \(I_{B-}\), recall that the inverting input is at virtual ground. This implies that the voltage across \(R_i\) must be zero, and therefore, the current through \(R_i\) must be zero. Consequently, all of \(I_{B-}\) flows through \(R_f\). This creates a relative negative potential at the output.
\[ V_{out -offset 3} = −I_{B-} R_f \label{5.15} \]
So the combination of the input bias current effects is:
\[ V_{out -offset(I_B)} = | I_{B+} R_{off} A_{noise} − I_{B-} R_f | \label{5.16} \]
Expanding this produces
\[ V_{out -offset(I_B)} = I_{B+} R_{off} \frac{R_i+R_f}{R_i} − I_{B-} R_f \nonumber \]
\[ V_{out -offset(I_B)} = \left( I_{B+} R_{off} \frac{R_i+R_f}{R_i R_f} −I_{B-}\right) R_f \nonumber \]
By noting the product-sum rule for resistor combination \(R_i\), \(R_f\), this can be further simplified to
\[ V_{out -offset(I_B)} = \left(\frac{I_{B+} R_{off}}{R_i || R_f} −I_{B-}\right) R_f \label{5.17} \]
If \(R_{off}\) is set to equal \(R_i || R_f\), this reduces to:
\[ V_{out -offset(I_B)} = (I_{B+} − I_{B-} )R_f \nonumber \]
By definition,
\[ I_{OS} = | I_{B+} − I_{B-} | \nonumber \]
so we finally come to
\[ V_{out−offset(I_B)} = I_{OS} R_f \label{5.18} \]
If it is possible, \(R_{off}\) should be set to \(R_i || R_f\). This drastically reduces the effect of the input bias current. Note that the value of \(R_{off}\) includes the driving source internal resistance. If \(R_i || R_f = 2 k\Omega\) and the driving source resistance is 100 \(\Omega\), the required resistance value would be 1.9 k\(\Omega\). If setting \(R_{off}\) to the optimum value is not possible, you can at least reduce the effect of \(I_B\) by using a partial value. Also, note that it is possible to determine the polarity of the offset caused by \(I_{B+}\) and \(I_{B-}\) (Equation \ref{5.17}) if actual currents and the type of device used in the diff amp stage are known. The circuit of Figure \(\PageIndex{1}\) assumes that NPN devices are being used, hence the currents are drawn as entering the op amp. PNP input devices would produce the opposite polarity. Typically, though, we don't have precise values for \(I_{B+}\) and \(I_{B-}\), and thus can only compute the worst-case magnitude.
For a final result, we may combine our components:
\[ V_{out−offset} = V_{OS} A_{noise} + I_{OS} R_f \label{5.19} \]
if \(R_{off} = R_i || R_f \), and
\[ V_{out−offset} = V_{OS} A_{noise} +|I_{B+} R_{off} A_{noise} – I_{B} R_f| \label{5.20} \]
if \(R_{off} ≠ R_i || R_f \).
There is one special case involving the selection of Roff, and that deals with a voltage follower. Normally for a follower, \(R_f = 0 \Omega\). What if the driving source resistance is perhaps 0 \(\Omega\)? The calculation would require an \(R_{off}\) of 0 \(\Omega\), and thus a -50 \(\Omega\) resistor to compensate for the source resistance. This is of course, impossible! To compensate for the 50 \(\Omega\) source, use 50 \(\Omega\) for \(R_f\). The circuit gain will still be unity, but \(I_B\) will now be compensated for. This is shown in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Offset compensation for a follower.
Example \(\PageIndex{1}\)
Determine the typical output offset voltage for the circuit of Figure \(\PageIndex{3}\) if \(R_{off}\) is 0 \(\Omega\). Then determine an optimum size for \(R_{off}\) and calculate the new offset.
From the data sheet for the 5534, we find \(V_{OS} = 0.5 mV\), \(I_{OS} = 10 nA\), and \(I_B = 800 nA\). Because this is an approximation, assume \(I_{B+} = I_{B-} = I_{B}\).
\[ A_{noise} = 1+ \frac{R_f}{R_i} \nonumber \]
\[ A_{noise} = 1+ \frac{10 k}{1 k} \nonumber \]
\[ A_{noise} = 11 \nonumber \]
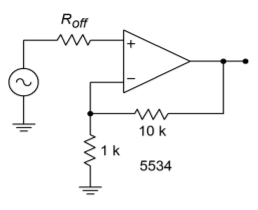
Figure \(\PageIndex{3}\): Circuit for Example \(\PageIndex{1}\).
\[ V_{out -offset} = V_{OS} A_{noise} + |I_{B+} R_{off} A_{noise} − I_{B-} R_f| \nonumber \]
\[ V_{out -offset} = 0.5mV\times 11+|800 nA\times 0\times 11−800 n A\times 10 k| \nonumber \]
\[ V_{out -offset} = 5.5mV+8mV \nonumber \]
\[ V_{out -offset} =13.5 mV \nonumber \]
Remember, this is the magnitude of the offset, it could be anywhere within \(\pm\)13.5 mV. It might be worse if this is not a typical device. Now we find the optimum offset compensating resistor:
\[ R_{off} = R_i || R_f \nonumber \]
\[ R_{off} = 1 k || 10 k \nonumber \]
\[ R_{off} = 909 \Omega \nonumber \]
For this case, the offset Equation reduces to
\[ V_{out−offset} = V_{OS} A_{noise} + I_{OS} R_f \nonumber \]
\[ V_{out−offset} = 0.5mV\times 11+10 nA\times 10 k \nonumber \]
\[ V_{out−offset} = 5.5mV+100\mu V \nonumber \]
\[ V_{out−offset} = 5.6mV \nonumber \]
By adding \(R_{off}\), the output offset voltage is more than halved. This may lead you to think that it is always wise to add \(R_{off}\). Such is not the case. There are two times when you may prefer to leave it out: 1) to optimize noise characteristics, as we will see shortly, and 2) when using FET input op amps. FET input devices have very small input bias and offset currents to begin with, so their effect is negligible when using typical resistor values.
Example \(\PageIndex{2}\)
The circuit of Figure \(\PageIndex{4}\) is used as part of a measurement system. Assuming that the DC input signal is 3 mV, how much uncertainty is there in the output voltage typically?
The desired output from the amplifier is
\[ V_{out} = A_v V_{in} \nonumber \]
\[ V_{out} = − \frac{R_f}{R_i} V_{in} \nonumber \]
\[ V_{out} = − \frac{20 k}{5 k} 3 mV \nonumber \]
\[ V_{out} = −12 mV \nonumber \]
The typical specs for the 411 are \(V_{OS} = 0.8 mV\), \(I_{OS} = 25 pA\), \(I_B = 50 pA\)
\[ A_{noise} = 1+ \frac{R_f}{R_i} \nonumber \]
\[ A_{noise} = 1+ \frac{20 k}{5 k} \nonumber \]
\[ A_{noise} = 5 \nonumber \]
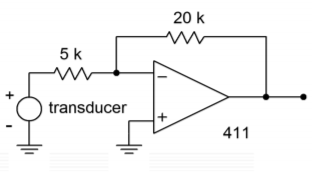
Figure \(\PageIndex{4}\): Circuit for Example \(\PageIndex{2}\).
\[ V_{out -offset} = V_{OS} A_{noise} +|I_{B+} R_{off} A_{noise} − I_{B-}R_f| \nonumber \]
\[ V_{out -offset} = 0.8mV\times 5+| 50 pA\times 0\times 11−50 pA\times 20 k | \nonumber \]
\[ V_{out -offset} = 4 mV+1\mu V \nonumber \]
\[ V_{out -offset} = 4 mV \nonumber \]
The output can vary by as much as \(\pm\)4 mV. As this a DC measurement system, the results are devastating. The output can be anywhere from -12 mV - 4 mV = -16 mV, to -12 mV + 4 mV = -8 mV. That's a 2:1 spread, and it's caused solely by the op amp. Note that the addition of \(R_{off}\) would have little effect here. Because the 411 uses a FET input, its \(I_B\) contribution is only 1 \(\mu\)V.
So, then, how do you keep output offsets to a minimum? First and foremost, make sure that the op amp chosen has low \(I_{OS}\) and \(V_{OS}\) ratings. Second, use the offset compensation resistor, \(R_{off}\). Third, keep the circuit resistances as low as possible. Finally, if the output offset is still too large, it can be reduced by manually nulling the circuit.
Nulling involves summing in a small signal that is of opposite polarity to the existing offset. By doing this, the new signal will completely cancel the offset and the output will show 0 V DC. This is much easier than it sounds. Most op amps have connections for null circuits. These are specified by the manufacturer and usually consist of a single potentiometer and perhaps one or two resistors. An example nulling connection is shown in Figure \(\PageIndex{5}\). Usually the potentiometer is a multi-turn trim type to allow for fine adjustment. To null the circuit, the technician monitors the output with a very sensitive DC voltmeter. The input is grounded (or perhaps tied to ground through a resistor equal to the driving source resistance if it's large). The potentiometer is then adjusted until the meter reads zero.
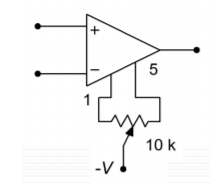
Figure \(\PageIndex{5}\): A typical nulling connection.
The drawback to this procedure is that it requires someone (or perhaps some thing) to perform the nulling. Also, the unit will require periodic adjustment to compensate for aging and environmental effects.
Computer Simulation
As stated, it is very important to match the input resistors in order to keep offsets low. This can be seen clearly in the simulation shown in Figure \(\PageIndex{6}\). A noninverting voltage amplifier is modeled here using the 741. In order to focus on the offset current effect, the contribution of \(V_{OS}\) is kept small by keeping the voltage gain low. The simulation is run twice for DC Operating Point. In the case where the resistances are matched, the DC output voltage is less than 1 mV. For the unmatched case, \(R_{off}\) is set to a fraction of an Ohm. The resulting DC output voltage is much larger at approximately 17 mV. It is worthy to note that this is approximately equal to \(I_{bias}\) times \(R_f\) (80 nA times 200 k\(\Omega\)). This simulation also points out the poor performance caused by excessively large resistor values. If the simulation is re-run with the resistors scaled down in size, the offsets will be lessened.
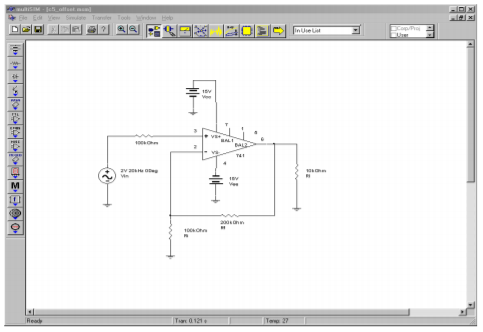
Figure \(\PageIndex{6a}\): Multisim schematic for offset simulation.
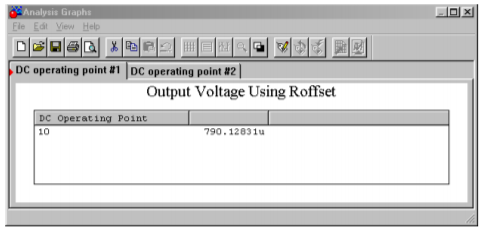
Figure \(\PageIndex{6b}\): Results with offset resistor.
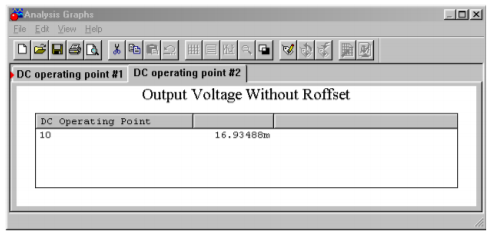
Figure \(\PageIndex{6c}\): Results without offset resistor.


