2.12: Exercises
- Page ID
- 41020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- A coaxial line is short-circuited at one end and is filled with a dielectric with a relative permittivity of \(64\). [Parallels Example 2.1.1]
- What is the free-space wavelength at \(18\text{ GHz}\)?
- What is the wavelength in the dielectric-filled coaxial line at \(18\text{ GHz}\)?
- The first resonance of the coaxial resonator is at \(18\text{ GHz}\). What is the physical length of the resonator?
- A transmission line has the following \(RLGC\) parameters: \(R = 100\:\Omega\text{/m},\: L = 85\text{ nH/m},\: G = 1\text{ S/m},\) and \(C = 150\text{ pF/m}\). Consider a traveling wave on the transmission line with a frequency of \(1\text{ GHz}\). [Parallels Example 2.2.2]
- What is the attenuation constant?
- What is the phase constant?
- What is the phase velocity?
- What is the characteristic impedance of the line?
- What is the group velocity?
- A transmission line has the per-unit length parameters \(L = 85\text{ nH/m},\: G = 1\text{ S/m},\) and \(C = 150\text{ pF/m}\). Use a frequency of \(1\text{ GHz}\). [Parallels Example 2.2.2]
- What is the phase velocity if \(R = 0\:\Omega\text{/m}\)?
- What is the group velocity if \(R = 0\:\Omega\text{/m}\)?
- If \(R = 10\text{ k}\Omega\text{/m}\) what is the phase velocity?
- If \(R = 10\text{ k}\Omega\text{/m}\) what is the group velocity?
- A line is \(10\text{ cm}\) long and at the operating frequency the phase constant \(\beta\) is \(40\text{ rad/m}\). What is the electrical length of the line? [Parallels Example 2.1.2]
- A dielectric-filled lossless transmission line carrying a \(1\text{ GHz}\) signal has the parameters \(L = 80\text{ nH/m}\) and \(C = 200\text{ pF/m}\). When the dielectric is replaced by air the line’s capacitance is \(C_{\text{air}} = 50\text{ pF/m}\). What is the relative permittivity of the dielectric?
- A coaxial transmission line is filled with lossy dielectric material with a relative permittivity of \(5 −\jmath 0.2\). If the line is air-filled it would have a characteristic impedance of \(100\:\Omega\). What is the input impedance of the line if it is \(1\text{ km}\) long? Use reasonable approximations. [Hint: Does the termination matter?]
- A transmission line has the per unit length parameters \(R = 2\Omega\text{/cm},\: L=100\text{ nH/m},\: G = 1\text{ mS/m},\: C = 200\text{ pF/m}\).
- What is the propagation constant of the line at \(5\text{ GHz}\)?
- What is the characteristic impedance of the line at \(5\text{ GHz}\)?
- Plot the magnitude of the characteristic impedance versus frequency from \(100\text{ MHz}\) to \(10\text{ GHz}\).
- A line is \(20\text{ cm}\) long and at \(1\text{ GHz}\) the phase constant \(\beta\) is \(20\text{ rad/m}\). What is the electrical length of the line in degrees?
- What is the electrical length of a line that is a quarter of a wavelength long,
- in degrees?
- in radians?
- A lossless transmission line has an inductance of \(8\text{ nH/cm}\) and a capacitance of \(40\text{ pF/cm}\).
- What is the characteristic impedance of the line?
- What is the phase velocity on the line at \(1\text{ GHz}\)?
- A \(50\:\Omega\) coaxial airline is a coaxial line without a dielectric (i.e., it is air-filled) and with thin dielectric discs supporting the inner conductor have negligible effect. If the air is replaced by a dielectric having a relative permittivity of \(20\), what is the characteristic impedance of the dielectric-filled line?
- A transmission line has an attenuation of \(2\text{ dB/m}\) and a phase constant of \(25\text{ radians/m}\) at \(2\text{ GHz}\). [Parallels Example 2.2.3]
- What is the complex propagation constant of the transmission line?
- If the capacitance of the line is \(50\text{ pF}\cdot\text{m}^{−1}\) and \(G = 0\), what is the characteristic impedance of the line?
- A very low-loss microstrip transmission line has the following per unit length parameters: \(R = 2\:\Omega\text{/m},\: L = 80\text{ nH/m},\: C = 200\text{ pF/m},\) and \(G = 1\:\mu\text{S/m}\).
- What is the characteristic impedance of the line if loss is ignored?
- What is the attenuation constant due to conductor loss?
- What is the attenuation constant due to dielectric loss?
- A lossless transmission line carrying a \(1\text{ GHz}\) signal has the following per unit length parameters: \(L = 80\text{ nH/m},\: C = 200\text{ pF/m}\).
- What is the attenuation constant?
- What is the phase constant?
- What is the phase velocity?
- What is its characteristic impedance?
- A transmission line has a characteristic impedance \(Z_{0}\) and is terminated in a load with a reflection coefficient of \(0.8\angle 45^{\circ}\). A forward-traveling voltage wave on the line has a power of \(1\text{ dBm}\).
- How much power is reflected by the load?
- What is the power delivered to the load?
- A transmission line has an attenuation of \(0.2\text{ dB/cm}\) and a phase constant of \(50\text{ radians/m}\) at \(1\text{ GHz}\).
- What is the complex propagation constant of the transmission line?
- If the capacitance of the line is \(100\text{ pF/m}\) and \(G = 0\), what is the complex characteristic impedance of the line?
- If the line is driven by a source modeled as an ideal voltage and a series impedance, what is the impedance of the source for maximum transfer of power to the transmission line?
- If \(1\text{ W}\) is delivered (i.e. in the forward-traveling wave) to the transmission line by the generator, what is the power in the forward-traveling wave on the line at \(2\text{ m}\) from the generator?
- The transmission line shown in Figure 2.5.1 consists of a source with Thevenin impedance \(Z_{1} = 40\:\Omega\) and source \(E = 5\text{ V}\) (peak) connected to a \(\lambda/4\) long line of characteristic impedance \(Z_{01} = 50\:\Omega\), which in turn is connected to an infinitely long line of characteristic impedance \(Z_{02} = 100\:\Omega\). The transmission lines are lossless. Two reference planes are shown in Figure 2.5.1. At reference plane \(\mathsf{1}\) the incident power is \(P_{I1}\), the reflected power is \(P_{R1}\), and the transmitted power is \(P_{T1}\). \(P_{I2},\: P_{R2},\) and \((P_{T2})\) are similar quantities at reference plane \(\mathsf{2}\). [Parallels Examples 2.6.4 and 2.6.6]
- What is \(P_{I1}\)?
- What is \(P_{T2}\)?
- A lossless, \(10\text{ cm}\)-long, \(75\:\Omega\) transmission line is driven by a \(1\text{ GHz}\) generator with a Thevenin equivalent impedance of \(50\:\Omega\). The maximum power that can be delivered to a load attached to the generator is \(2\text{ W}\). The line is terminated in a load that has a complex reflection coefficient (referred to \(50\:\Omega\)) of \(0.65 +\jmath 0.65\). The effective relative permittivity, \(\varepsilon_{e}\), of the non-magnetic transmission line is \(2.0\).
- Calculate the forward-traveling voltage wave (at the generator end of the transmission line). Ignore reflections from the load at the end of the \(75\:\Omega\) line.
- What is the load impedance?
- What is the wavelength of the forward-traveling voltage wave?
- What is the VSWR on the line?
- What is line’s propagation constant?
- What is the input reflection coefficient (at the generator end) of the line?
- What is the power delivered to the load?
- The first resonance of a lossless non-magnetic open-circuited transmission line is at \(30\text{ GHz}\). The effective relative permittivity of the line is \(12\).
- What is the resonator’s input impedance?
- Draw its LC equivalent circuit.
- What is its electrical length?
- What is its physical length?
- An open-circuited transmission line is used as a resonator. What is the electrical length of the line at its first resonance?
- The second resonance of an open-circuited transmission line is used as a resonator.
- What is its input impedance?
- What is its electrical length?
- A lossless transmission line is driven by a \(1\text{ GHz}\) generator having a Thevenin equivalent impedance of \(50\:\Omega\). The transmission line is lossless, has a characteristic impedance of \(75\:\Omega\), and is infinitely long. The maximum power that can be delivered to a load attached to the generator is \(2\text{ W}\).
- What is the total (phasor) voltage at the input to the transmission line?
- What is the magnitude of the forward-traveling voltage wave at the generator side of the line?
- What is the magnitude of the forward-traveling current wave at the generator side of the line?
- A transmission line is terminated in a short circuit. What is the ratio of the forward- and backward-traveling voltage waves at the termination? [Parallels Example 2.3.1]
- A \(50\:\Omega\) transmission line is terminated in a \(40\:\Omega\) load. What is the ratio of the forward- to the backward-traveling voltage waves at the termination? [Parallels Example 2.3.1]
- A \(50\:\Omega\) transmission line is terminated in an open circuit. What is the ratio of the forward-to the backward-traveling voltage waves at the termination? [Parallels Example 2.3.1]
- The resonator below is constructed from a \(3.0\text{ cm}\) length of \(100\:\Omega\) air-filled coaxial line, shorted at one end and terminated with a capacitor at the other end.
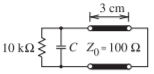
Figure \(\PageIndex{1}\)
- What is the lowest resonant frequency of this circuit without the capacitor (ignore the \(10\text{ k}\Omega\) resistor)?
- What is the capacitor value to achieve the lowest-order resonance at \(6.0\text{ GHz}\) (ignore the \(10\text{ k}\Omega\) resistor)?
- Assume that loss is introduced by placing a \(10\text{ k}\Omega\) resistor in parallel with the capacitor. What is the \(Q\) of the circuit?
- Approximately what is the bandwidth of the circuit?
- A \(50\:\Omega\) transmission line is terminated in a load that results in a reflection coefficient of \(0.5+\jmath 0.5\).
- What is the load impedance?
- What is the \(\text{VSWR}\) on the line?
- What is the input impedance if the line is one-half wavelength long?
- Communication filters are often constructed using several shorted transmission line resonators that are coupled by passive elements such as capacitors. Consider a coaxial line that is short-circuited at one end. The dielectric filling the coaxial line has a relative permittivity of \(64\) and the resonator is to be designed to resonate at a center frequency, \(f_{0}\), of \(800\text{ MHz}\). [Parallels Example 2.7.2]
- What is the wavelength in the dielectricfilled coaxial line?
- What is the form of the equivalent circuit (in terms of inductors and capacitors) of the one-quarter wavelength long resonator if the coaxial line is lossless?
- What is the length of the resonator?
- If the diameter of the inner conductor of the coaxial line is \(2\text{ mm}\) and the inside diameter of the outer conductor is \(5\text{ mm}\), what is the characteristic impedance of the coaxial line?
- Calculate the input admittance of the dielectric-filled coaxial line at \(0.99f_{0},\: f_{0},\) and \(1.01f_{0}\). Determine the numerical derivative of the line admittance at \(f_{0}\).
- Derive the values of the equivalent circuit of the resonator at the resonant frequency and derive the equivalent circuit of the resonator. Hint: Match the derivative expression derived in (e) with the actual derivative derived in Example 2.7.2.
- Develop an analytic formula relating a reflection coefficient \((\Gamma_{1})\) in one reference system \((Z_{01})\) to a reflection coefficient \((\Gamma_{2})\) in another reference system \((Z_{02})\).
- A line has a characteristic impedance \(Z_{0}\) and is terminated in a load with a reflection coefficient of \(0.8\). A forward-traveling voltage wave on the line has a power of \(1\text{ W}\).
- How much power is reflected by the load?
- What is the power delivered to the load?
- A load consists of a shunt connection of a capacitor of \(10\text{ pF}\) and a resistor of \(25\:\Omega\). The load terminates a lossless \(50\:\Omega\) transmission line. The operating frequency is \(1\text{ GHz}\). [Parallels Example 2.3.2]
- What is the impedance of the load?
- What is the normalized impedance of the load (normalized to the characteristic impedance of the line)?
- What is the reflection coefficient of the load?
- What is the current reflection coefficient of the load?
- What is the standing wave ratio (SWR)?
- What is the current standing wave ratio (ISWR)?
- A \(50\:\Omega\) air-filled transmission line is connected between a \(40\text{ GHz}\) source with a Thevenin equivalent impedance of \(50\:\Omega\) and a load. The SWR on the line is \(3.5\).
- What is the magnitude of the reflection coefficient, \(\Gamma_{L}\), at the load?
- What is the phase constant, \(\beta\), of the line?
- If the first minimum of the standing wave voltage on the transmission line is \(2\text{ mm}\) from the load, determine the electrical distance (in degrees) of the SWR minimum from the load.
- Determine the angle of \(\Gamma_{L}\) at the load.
- What is \(\Gamma_{L}\) in magnitude-phase form?
- What is \(\Gamma_{L}\) in rectangular form?
- Determine the load impedance, \(Z_{L}\).
- A load consists of a resistor of \(100\:\Omega\) in parallel with a \(5\text{ pF}\) capacitor with an electrical signal at \(2\text{ GHz}\).
- What is the load impedance?
- What is the reflection coefficient in a \(50\:\Omega\) reference system?
- What is the SWR on a \(50\:\Omega\) transmission line connected to the load?
- An amplifier is connected to a load by a transmission line matched to the amplifier. If the SWR on the line is \(1.5\), what percentage of the available amplifier power is absorbed by the load?
- An output amplifier can tolerate a mismatch with a maximum SWR of \(2.0\). The amplifier is characterized by a Thevenin equivalent circuit with an impedance of \(50\:\Omega\) and is connected directly to an antenna characterized by a load resistance \(R_{L}\). Determine the tolerance limits on \(R_{L}\) so that the amplifier does not self-destruct.
- A load has a reflection coefficient of \(0.5\) when referred to \(50\:\Omega\). The load is placed at the end of a \(100\:\Omega\)-transmission line.
- What is the complex ratio of the forward-traveling wave to the backward-traveling wave on the \(100\:\Omega\) line at the load end of the line?
- What is the VSWR on the \(100\:\Omega\) line?
- A load has a reflection coefficient of \(0.5\) when referred to \(50\:\Omega\). The load is at the end of a line with a \(50\:\Omega\) characteristic impedance.
- If the line has an electrical length of \(45^{\circ}\), what is the reflection coefficient calculated at the input of the line?
- What is the VSWR on the \(50\:\Omega\) line?
- A \(100\:\Omega\) resistor in parallel with a \(5\text{ pF}\) capacitor terminates a \(100\:\Omega\) transmission line. Calculate the SWR on the line at \(2\text{ GHz}\).
- A lossless \(50\:\Omega\) transmission line has a \(50\:\Omega\) generator at one end and is terminated in \(100\:\Omega\). What is the VSWR on the line?
- A lossless \(75\:\Omega\) line is driven by a \(75\:\Omega\) generator. The line is terminated in a load that with a reflection coefficient (referred to \(50\:\Omega\)) of \(0.5 + \jmath 0.5\). What is the VSWR on the line?
- A load with a \(20\text{ pF}\) capacitor in parallel with a \(50\:\Omega\) resistor terminates a \(25\:\Omega\) line. The operating frequency is \(5\text{ GHz}\). [Parallels Example 2.3.3]
- What is the VSWR?
- What is ISWR?
- A load \(Z_{L} = 55−\jmath 55\:\Omega\) and the system reference impedance, \(Z_{0}\), is \(50\:\Omega\). [Parallels Example 2.3.4]
- What is the load reflection coefficient \(\Gamma_{L}\)?
- What is the current reflection coefficient?
- What is the VSWR on the line?
- What is the ISWR on the line?
- Now consider a source connected directly to the load. The source has a Thevenin equivalent impedance \(Z_{G} = 60\:\Omega\) and an available power of \(1\text{ W}\). Use \(\Gamma_{L}\) to find the power delivered to \(Z_{L}\).
- What is the total power absorbed by \(Z_{G}\)?
- A slotted line, as shown in Figure 2.3.7(c), is used to characterize a \(50\:\Omega\) line terminated in a load \(Z_{L}\). \(V_{\text{max}} = 1\text{ V}\) and \(V_{\text{min}} = 0.1\text{ V}\), and the first minimum is \(5\text{ cm}\) from the load. The guide wavelength is \(30\text{ cm}\). What is \(Z_{L}\)? [Parallels Example 2.3.5]
- A shorted coaxial line is used as a resonator. The first resonance is determined to be a parallel resonance and is at \(1\text{ GHz}\).
- Draw the lumped-element equivalent circuit of the resonator.
- What is the electrical length of the resonator?
- What is the impedance looking into the line at resonance?
- If the resonator is \(\lambda/4\) longer, what is the impedance of the resonator now?
- A load of \(100\:\Omega\) is to be matched to a transmission line with a characteristic impedance of \(50\:\Omega\). Use a quarter-wave transformer. What is the characteristic impedance of the quarter-wave transformer?
- Determine the characteristic impedance of a quarter-wave transformer used to match a load of \(50\:\Omega\) to a generator with a Thevenin equivalent impedance of \(75\:\Omega\).
- A transmission line is to be inserted between a \(5\:\Omega\) line and a \(50\:\Omega\) load so that there is maximum power transfer to the \(50\:\Omega\) load at \(20\text{ GHz}\).
- How long is the inserted line in terms of wavelengths at \(20\text{ GHz}\)?
- What is the characteristic impedance of the line at \(20\text{ GHz}\)?
- The resonator below is constructed from a \(3.0\text{ cm}\) length of \(100\:\Omega\) air-filled coaxial line shorted at one end and terminated with a capacitor at the other end:

Figure \(\PageIndex{2}\)
- What is the lowest resonant frequency of this circuit without the capacitor (ignore the resistor)?
- What is the capacitor value required to achieve resonance at \(6.0\text{ GHz}\)?
- Assume that loss is introduced by placing a \(10\text{ k}\Omega\) resistor in parallel with the capacitor. What is the \(Q\) of the circuit?
- What is the bandwidth of the circuit?
- A coaxial transmission line is filled with lossy material with a relative permittivity of \(5 −\jmath 0.2\). If the line is air-filled it would have a characteristic impedance of \(100\:\Omega\).
- What is the characteristic impedance of the dielectric-filled line?
- What is the propagation constant at \(500\text{ MHz}\)?
- What is the input impedance of the line if it has an electrical length of \(280^{\circ}\) and is terminated in a \(35\:\Omega\) resistor?
- A coaxial line is filled with a very slightly lossy material with a relative permittivity of \(5\). The line would have a characteristic impedance of \(100\:\Omega\) if it was air-filled.
- What is the characteristic impedance of the dielectric-filled line?
- What is the propagation constant at \(500\text{ MHz}\)? Use the fact that the velocity of an EM wave in a lossless air-filled line is the same as that of free-space propagation in air.
- What is the input impedance of the line if it has an electrical length of \(90^{\circ}\) and it is terminated in a \(35\:\Omega\) resistor?
- What is the input impedance of the line if it has an electrical length of \(180^{\circ}\) and is terminated in an impedance \(\jmath 35\:\Omega\)?
- What is the input impedance of the line if it is \(1\text{ km}\) long? Use reasonable approximations.
- A lossy transmission line with a characteristic impedance of \(60 −\jmath 2\:\Omega\) is driven by a generator with a Thevenin equivalent impedance \(Z_{g}\). If the line is infinitely long, what is \(Z_{g}\) for maximum power transfer from the generator to the line?
- A \(25\:\Omega\)-transmission line is driven by a generator with an available power of \(23\text{ dBm}\) and a Thevenin equivalent impedance of \(60\:\Omega\). [Parallels Example 2.6.3]
- What is the Thevenin equivalent generator voltage?
- What is the magnitude of the forward-traveling voltage wave on the line? Assume the line is infinitely long.
- What is the power of the forward-traveling voltage wave?
- A open-circuited coaxial line is used as a resonator. The first resonance is a series resonance at \(2\text{ GHz}\). [Parallels Example 2.5.1]
- Draw the lumped-element equivalent circuit of the resonator.
- What is the resonator’s electrical length?
- What is the impedance looking into the line at resonance?
- If the resonator is \(3\lambda_{g}/4\) longer, what is the input impedance of the resonator?
- The forward-traveling wave on a \(60\:\Omega\) line has a power of \(2\text{ mW}\). The line is terminated in a resistance of \(50\:\Omega\). How much power is delivered to the \(50\:\Omega\) load.
- The forward-traveling wave on a \(40\:\Omega\) line has a power of \(2\text{ mW}\). The line is terminated in a resistance of \(60\:\Omega\). How much power is in the backward traveling wave?
- The forward-traveling wave on a \(60\:\Omega\) line has a power of \(2\text{ mW}\). The line is terminated in a resistance of \(50\:\Omega\). Draw the lumped-element equivalent circuit at the interface of the line and the load. [Parallels Example 2.6.1]
- A source is connected to a load by a one wavelength long transmission line having a loss of \(1.5\text{ dB}\). The source reflection coefficient (referred to the transmission line) is \(0.2\) and the load reflection coefficient is \(0.5\).
- What is the transmission coefficient?
- Draw the bounce diagram using the transmission and reflection coefficients. Determine the overall effective transmission coefficient from the source to the load. Calculate the power delivered to the load from a source with an available power of \(600\text{ mW}\).
- Consider a coaxial line that is short-circuited at one end. The dielectric filling the line has \(\varepsilon_{r} = 20\) and the line has its lowest frequency resonance at \(2.4\text{ GHz}\). [Parallels Example 2.7.1]
- What is the guide wavelength?
- Draw the resonator’s equivalent circuit.
- What is the resonator’s physical length?
- Consider a lossless coaxial line that is open-circuited at one end and is used as a resonator that is resonant at \(f_{0} = 2.4\text{ GHz}\). The line’s dielectric has \(\varepsilon_{r} = 81\). [Parallels Example 2.7.2]
- What is the wavelength in the line?
- Draw the lumped-element equivalent circuit of a \(\lambda_{g}/4\) long resonator?
- What is the resonator’s physical length?
- What is the derivative with respect to frequency of the admittance of the \(LC\) equivalent circuit developed in (b).
- If the diameter of the inner conductor of the line is \(1\text{ mm}\) and the inside diameter of the outer conductor is \(3\text{ mm}\), what is the characteristic impedance of the line?
- Determine the numerical frequency derivative of the line admittance at \(f_{0}\).
- Derive the values of the equivalent circuit of the resonator at resonance.
- Develop the lumped-element model of a half wavelength long line having characteristic impedance \(Z_{0}\). [Parallels Example 2.7.3]
- The diameter of the inner conductor of a coaxial line is \(2\text{ mm}\) and the interior diameter of the outer conductor \(8\text{ mm}\). The coaxial line is filled with polyimide which has a relative permittivity of \(3.2\).
- What is the characteristic impedance of the line?
- Describe the conditions by which a non-TEM mode can be supported. Refer to two different families of higher-order modes.
- For the coaxial line here, at what frequency will a second propagating mode be first supported?
2.12.1 Exercises By Section
\(†\)challenging, \(‡\)very challenging
\(§2.1\: 1\)
\(§2.2\: 2†, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14†, 15\)
\(§2.3\: 16†, 17, 18‡, 19‡, 20, 21, 22, 23, 24, 25, 26†, 27‡, 28‡, 29, 30†, 31†, 32‡, 33‡, 34†, 35†, 36†, 37, 38, 39, 40, 41, 42, 43\)
\(§2.4\: 44†, 45, 46, 47\)
\(§2.5\: 48‡, 49†, 50†, 51, 52‡, 53\)
\(§2.6\: 54, 55, 56, 57†\)
\(§2.7\: 58, 59†, 60\)
\(§2.9\: 61\)
2.12.2 Answers to Selected Exercises
- \(11.2\:\Omega\)
- \(0.23+\jmath 25\text{ m}^{-1}\)
- (b) \(74.0\text{ mW}\)
- (c) \(1.17\text{ cm}\)
- (e) \(\jmath 4.55\cdot 10^{-11}\text{ S}\cdot\text{ s}\)
- (f) \(0.544+\jmath 0.116\)
- (f) \(41.45\)
- \(25\:\Omega\leq Z_{L}\leq 100\:\Omega\)
- \(61.2\:\Omega\)
- \(354.2\text{ mW}\)


