5.6: Formulas for Impedance of Coupled Microstrip Lines
- Page ID
- 41059
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Formulas for the characteristic impedance and effective permittivity of symmetric coupled microstrip lines, with the cross section shown in Figure \(\PageIndex{1}\), were developed by Hammerstad and Jensen [2] based on the concept of even and odd modes. The formulas are accurate to better than \(1\%\) for \(0.1 ≤ u ≤ 10\) and \(g > 0.01\), where \(u\) is the normalized width, and \(g\) is the normalized gap:
\[\label{eq:1}u=w/h\quad g=s/h \]
In the following, \(Z_{0}\) and \(\varepsilon_{e}\) refer to the characteristic impedance and effective permittivity of an individual microstrip line with a normalized width of \(u\) on a substrate with a relative dielectric constant of \(\varepsilon_{r}\).
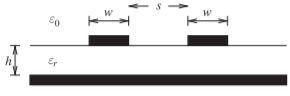
Figure \(\PageIndex{1}\): Cross section of symmetrically coupled microstrip lines.
5.6.1 Even-Mode Coupled-Line Parameters
The even-mode characteristic impedance is
\[\label{eq:2}Z_{0e}(u,g)=Z_{01e}(u,g)/\sqrt{\varepsilon_{ee}(u, g,\varepsilon_{r})} \]
where \(\varepsilon_{ee}\) is the effective relative permittivity of the even mode and \(Z_{01e}\) is the even-mode characteristic impedance with the dielectric replaced by free space:
\[\label{eq:3}Z_{01e}(u,g)=\frac{Z_{0}(u)}{1-Z_{0}(u)\phi_{e}(u,g)/\eta_{0}} \]
where
\[\label{eq:4}\phi_{e}(u,g)=\frac{\varphi(u)}{\psi(g)\{\alpha(g)u^{m(g)}+[1-\alpha(g)]u^{-m(g)}\}} \]
and \(\eta_{0} = 376.73\:\Omega\approx 377\:\Omega\) is the characteristic impedance of a TEM wave in a vacuum (i.e., free space). Now \(Z_{0}(u)\) is the free-space characteristic impedance of an individual microstrip line and is given by Equation (3.5.13). In Equations \(\eqref{eq:2}\) and \(\eqref{eq:3}\), the effective permittivity of the even mode is
\[\label{eq:5}\varepsilon_{ee}(u,g,\varepsilon_{r})=\frac{\varepsilon_{r}+1}{2}+\frac{\varepsilon_{r}-1}{2}F_{e}(u,g,\varepsilon_{r}) \]
where
\[\begin{align}\label{eq:6}F_{e}(u,g,\varepsilon_{r})&=\left[1+\frac{10}{\mu(u,g)}\right]^{-a(u)b(\varepsilon_{r})} \\ \label{eq:7} a(u)&=1+\frac{1}{49}\ln\left[\frac{u^{4}+\{u/52\}^{2}}{u^{4}+0.432}\right]+\frac{1}{18.7}\ln\left[1+\left(\frac{u}{18.1}\right)^{3}\right] \\ \label{eq:8} b(\epsilon_{r})&=0.564\left[\frac{\epsilon_{r}-0.9}{\epsilon_{r}+3}\right]^{0.053} \\ \label{eq:9}\varphi(u)&=0.8645u^{0.172} \\ \label{eq:10}\psi(g)&=1+\frac{g}{1.45}+\frac{g^{2.09}}{3.95} \\ \label{eq:11}\alpha(g)&=0.5\exp(-g) \\ \label{eq:12}m(g)&=0.2175+\left[4.113+\left(\frac{20.36}{g}\right)^{6}\right]^{-0.251}+\frac{1}{323}\ln\left[\frac{g^{10}}{1+(g/13.8)^{10}}\right] \\ \label{eq:13}\mu(u,g)&=g\exp (-g)+\frac{u(20+g^{2})}{10+g^{2}}\end{align} \]
5.6.2 Odd-Mode Coupled-Line Parameters
The odd-mode characteristic impedance is
\[\label{eq:14}Z_{0o}(u,g)=Z_{01o}(u,g)/\sqrt{\varepsilon_{eo}(u,g,\varepsilon_{r})} \]
where \(\varepsilon_{eo}\) is the effective relative permittivity of the odd mode and \(Z_{01o}\) is the odd-mode characteristic impedance with the dielectric replaced by free-space:
\[\label{eq:15}Z_{01o}(u,g)=\frac{Z_{0}(u)}{1-Z_{0}(u)\phi_{o}(u,g)/\eta_{0}} \]
\(Z_{0}(u)\) is the free-space characteristic impedance of an individual microstrip line and is given by Equation (3.5.13). In Equations \(\eqref{eq:14}\) and \(\eqref{eq:15}\), the effective permittivity of the odd mode is
\[\label{eq:16}\varepsilon_{eo}(u,g,\varepsilon_{r})=\frac{\varepsilon_{r}+1}{2}+\frac{\varepsilon_{r}-1}{2}F_{o}(u,g,\varepsilon_{r}) \]
where
\[\begin{align}\label{eq:17}F_{o}(u,g,\varepsilon_{r})&=f_{o}(u,g,\varepsilon_{r})(1+10/u)^{-a(u)b(\varepsilon_{r})} \\ \label{eq:18}\phi_{o}(u,g)&=\phi_{e}(u,g)-\frac{\theta(g)}{\psi(g)}\exp\left[\beta(g)u^{n(g)}\ln(u)\right] \\ \label{eq:19}\theta(g)&=1.729+1.175\ln\left(1+\frac{0.627}{g+0.327g^{2.17}}\right) \\ \beta(g)&=0.2306+\frac{1}{301.8}\ln\left[\frac{g^{10}}{1+(g/3.73)^{10}}\right] \\ \label{eq:20} &\quad+\frac{1}{5.3}\ln(1+0.646g^{1.175}) \\ n(g)&=\left\{\frac{1}{17.7}+\exp[-6.424-0.76\ln(g)-(g/0.23)^{5}]\right\} \\ \label{eq:21}&\quad\times\ln\left(\frac{10+68.3g^{2}}{1+32.5g^{3.093}}\right) \\ \label{eq:22}f_{o}(u,g,\varepsilon_{r})&=f_{o1}(g,\varepsilon_{r})\exp\left[p(g)\ln(u)+q(g)\sin\left(\pi\frac{\ln u}{\ln 10}\right)\right] \\ \label{eq:23} p(g)&=\exp(-0.745g^{0.295})/ \cosh(g^{0.68}) \\ \label{eq:24}f_{o1}(g,\varepsilon_{r})&=1-\exp\left\{-0.179g^{0.15}-\frac{0.328g^{r(g,\varepsilon_{r})}}{\ln[\exp(1)+(g/7)^{2.8}]}\right\} \\ \label{eq:25}r(g,\varepsilon_{r})&=1+0.15\left\{1-\frac{\exp[1-(\varepsilon_{r}-1)^{2}/8.2]}{1+g^{-6}}\right\} \\ \label{eq:26}q(g)&=\exp(-1.366-g) \end{align} \]
and \(a(u),\: b(\varepsilon_{r}),\) and \(\psi(g)\) are the same as for the even mode (see Section 5.6.1).
5.6.3 System Impedance of Coupled Lines
The system impedance of a pair of coupled lines is
\[\label{eq:27}Z_{0S}=\sqrt{Z_{0e}Z_{0o}} \]
This is derived in Section 5.7.1 where it is shown that there will be no odd-mode reflections, and even-mode reflections will be small, at the ports of a symmetrical coupled-line pair if each line of the directional coupler is terminated in an impedance \(Z_{0S}\). That is, \(Z_{0S}\) is the impedance required for matching. \(Z_{0}\) is the characteristic impedance of an individual line of the symmetrical coupled-line pair (when there is no coupling) and is only close to \(Z_{0S}\) when the separation, \(s\), of the lines is large.
5.6.4 Discussion
Normalized even- and odd-mode characteristic impedances of a pair of coupled lines are plotted in Figure \(\PageIndex{2}\) for various normalized widths \(u\)
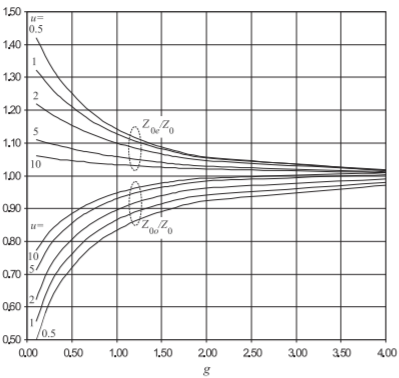
Figure \(\PageIndex{2}\): Normalized even-mode and odd-mode characteristic impedances of a pair of coupled microstrip lines \((\epsilon_{r} = 10)\).
\((= w/h)\) and as a function of normalized gap width \(g (= s/h)\). This plot illustrates the utility of using even- and odd-mode descriptions. In Figure \(\PageIndex{2}\), the even- and odd-mode impedances are normalized to the characteristic impedance of an individual line, \(Z_{0}\). When the lines are far apart (i.e., \(g\) is large), the even- and odd-mode impedances converge to the characteristic impedance of a single line. As the lines get closer, the gap narrows, and the even- and odd-mode impedances diverge in opposite directions. To obtain the characteristic impedances of a coupled line the characteristic impedance of a single microstrip line must be found. This was given in Section 3.5.3 and the key result is repeated in Figure \(\PageIndex{3}\).
In the even mode, more of the field is in the dielectric than with the odd mode. It is therefore not surprising that the effective permittivities of the two modes differ. The normalized coupled-line effective permittivities are shown in Figure \(\PageIndex{4}\). The deviation of the even- and odd-mode permittivities as the gap between the lines narrows is not as large as the change in the characteristic impedance. Also, there is a difference in the phase velocities of the two modes along the line, and this has an appreciable effect on the performance of components such as filters that use coupled lines as a functional component. At the first reading of the plot (\(\PageIndex{4}\)) it would seem that there is nonmonotonic behavior at low \(g\). This is an artifact of the normalization used, and the unnormalized permittivities are indeed monotonic with respect to both \(u\) and \(g\).
Figure \(\PageIndex{5}\) plots, as a function of normalized separation, \(g\), and for substrate permittivities ranging from \(4\) to \(20\), the even-mode and odd-mode characteristic impedances normalized to the characteristic impedance of a single strip for extremes of normalized widths (\(u = 0.5\) and \(u = 5\)). The figure highlights that the split of the even- and odd-mode characteristic impedances is almost solely dependent on geometry (i.e., the separation of the strips) and not the permittivity of the substrate. In the figure appropriate normalization is used to highlight this fact. There are four families of curves,

Figure \(\PageIndex{3}\): Normalized characteristic impedance and normalized effective permittivity of a microstrip line as a function of \(u = w/h\). For example, if \(u = 1\) and \(\varepsilon_{r} = 10\), then from the figure, \(Z_{0}\sqrt{\varepsilon_{e}} = 126\:\Omega\) and \(\varepsilon_{e}/\varepsilon_{r} = 0.671\); thus \(Z_{0} = 48.6\:\Omega\) and \(\varepsilon_{e} = 6.71\).

Figure \(\PageIndex{4}\): Normalized even-mode and odd-mode effective permittivity of a pair of coupled microstrip lines. The effective permittivity of an individual microstrip line with the same normalized width \(u\) is \(\varepsilon_{e}\).
two for the even-mode characteristic impedances and two for the odd-mode characteristic impedances. Each family comprises the results for three widely different permittivities of the dielectric (specifically \(\varepsilon_{r} = 4,\: 10,\) and \(20\)).
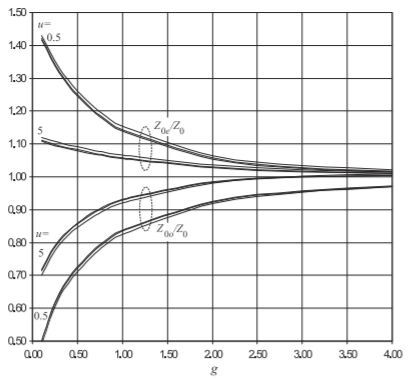
Figure \(\PageIndex{5}\): Normalized even-mode and odd-mode characteristic impedances of a pair of coupled microstrip lines for extremes of \(u\). Each family of three curves is for \(\varepsilon_{r} = 4,\: 10,\) and \(20\). \(Z_{0}\) is the characteristic impedance of an individual microstrip line with the same normalized width, \(u = w/h\). The strips have equal width.
A coupled line is constructed on an alumina substrate of thickness \(500\:\mu\text{m}\) and relative permittivity \(\varepsilon_{r} = 10\). The lines are \(500\:\mu\text{m}\) wide and the gap separation is \(250\:\mu\text{m}\). What are the even- and odd-mode characteristic impedances and effective permittivities of the coupled line?
Solution
The odd-mode characteristic impedance, \(Z_{0o}\), and even-mode characteristic impedance, \(Z_{0e}\), can be found using Figures \(\PageIndex{2}\) and \(\PageIndex{3}\). Now
\[u = w/h = (500\:\mu\text{m})/(500\:\mu\text{m}) = 1\quad\text{and}\quad g = s/h = (250\:\mu\text{m})/(500\:\mu\text{m}) = 0.5\nonumber \]
From Figure \(\PageIndex{2}\),
\[\label{eq:28}Z_{0e}/Z_{0} = 1.21\quad\text{and}\quad Z_{0o}/Z_{0} = 0.76 \]
where \(Z_{0}\) is the characteristic impedance of an individual line. From Figure \(\PageIndex{3}\), and using the curve for \(\varepsilon_{r} = 10\),
\[\label{eq:29}\varepsilon_{e}/\varepsilon_{r} = 0.671,\quad\text{and so}\quad \varepsilon_{e} = 10\times 0.671 = 6.71 \]
Also from Figure \(\PageIndex{3}\),
\[\label{eq:30}Z_{0}\sqrt{\varepsilon_{e}}= 126,\quad\text{and so}\quad Z_{0} = 126/\sqrt{6.71} = 48.6\:\Omega \]
Consequently, combining Equations \(\eqref{eq:28}\) and \(\eqref{eq:30}\),
\[\label{eq:31}Z_{0o}=37\:\Omega\quad\text{and}\quad Z_{0e}=59\:\Omega \]
The effective odd-mode and even-mode permittivities are obtained from Figure \(\PageIndex{4}\). The normalized even-mode effective permittivity is \(\varepsilon_{ee}/\varepsilon_{e} = 1.086\) and the normalized odd-mode effective permittivity is \(\varepsilon_{eo}/\varepsilon_{e} = 0.868\). Since \(\varepsilon_{e} = 6.71\), the final result is
\[\varepsilon_{ee}=7.28\quad\text{and}\quad\varepsilon_{eo}=5.82 \nonumber \]
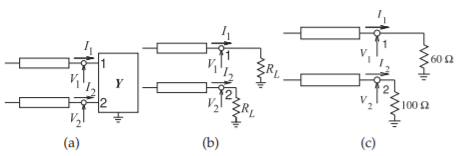
Figure \(\PageIndex{6}\): Terminated coupled lines: (a) with a load described by the y-parameter matrix \(\mathbf{Y}\); (b) symmetrical loads; (c) loads considered in example.
5.6.5 Summary
This section presented formulas and graphs for determining the frequency-independent parameters of coupled lines given their dimensions. Frequency dependence of these electrical parameters are discussed in [3, 4]. The effect of finite metallization thickness is also discussed in [3]. Synthesis of coupled lines, i.e. determining their physical dimensions given their desired electrical parameters, is undertaken in the context of their use and is generally based on approximate, but reasonably accurate, models of a pair of coupled lines. This will be considered in Section 5.9.


